Обозначим проекции на координатные оси, через.

Получим - эта формула является основной в векторном исчислении и называетсяРазложение вектора по ортам координатных осей. Числа называютсякоординатами вектора а.

Проекции вектора на оси координат называются его координатами. В этом заключается их геометрический смысл.

Векторное равенство иногда записывают в символическом виде .

Зная проекции вектора легко можно найти его длину, т.е. модуль. На основании теоремы о длине диагонали параллелепипеда .

Т.е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат. координат .

Пусть углы вектора с координатными осями соответственно равны . По свойству проекции вектора на ось имеем.(*)

Опр.12 Косинусы углов, которые вектор образует с осями координат, называются направляющими косинусами вектора.

Если вектор задан на плоскости, то .

Они обладают замечательным свойством:

.

Для .

Из формул (*) следует, что координатами единичного вектора являются направляющие косинусы, т.е. .

5. Действия над векторами в координатной форме

Для любой точки в ДСК координаты вектора ОМ- радиус –вектора являются её координатами

Если начало вектора не совпадает с началом координат, но известны координаты начальной A и конечной B точек, то координаты вектора представляют собой разности одноименных координат его начальной и конечной точек.

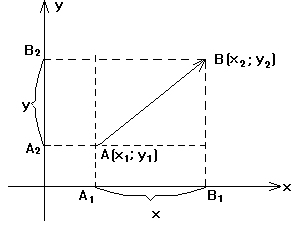
Пусть A(x₁;y₁),а B(x₂;y₂), тогда

.

Это в двумерном пространстве (R²).

Аналогично в трехмерном пространстве. Если ,, то

Если известны координаты вектора , то его модуль равен корню квадратному из суммы квадратов его координат.

.

Если , то.

Направляющие косинусы любого вектора вычисляются по нижеприведенным формулам:

.

Пустьи.

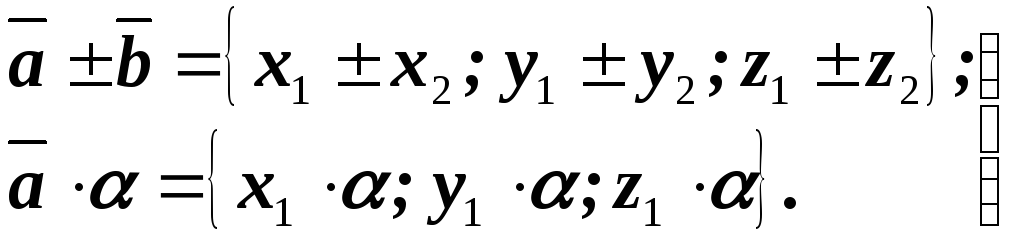
Если векторы иколлинеарны, то соответствующие координаты их пропорциональны: .

Верно и обратное, т.е. если выполняется соотношение ,то .

§3. N- мерное векторное пространство. Линейная зависимость и независимость векторов.

1. N- мерное векторное пространство.

2. Линейная зависимость и независимость векторов

3. Базис векторного пространства. Разложение вектора по базису

1.N- мерное векторное пространство

Пусть имеется система векторов:

Опр.13.Выражение вида: , (3.1) где-вещественные числа, называется линейной

комбинацией векторов.

Опр.14.Система векторов называетсялинейно независимой, если линейная комбинация (3.1) равна нулю при условии, что все =0, т.е. . (3.2)

Если линейная комбинация (3.1) равна нулю при условии, что хотя бы одно из чисел , то система векторов (3.1) называетсялинейно зависимой.

Если система содержит более одного вектора , то линейная зависимость её означает, что по крайней мере один из векторов системы может быть представлен в виде линейной комбинации других векторов системы. Действительно, пусть векторылинейно зависимы и пусть. Тогда в равенстве (3.2) можно обе части разделить наи выразить векторчерез остальные векторы; т.е. представить его в виде их линейной комбинации:

.

Обозначив ;; …, получим

. (3.3)

Если все члены равенства (3.3) перенести в одну сторону, то получим , т.е. линейная комбинация равна нулю при условии, что коэффициент при вектореотличен от нуля. Он равен (-1).

Вывод. Если хотя бы один из векторов является их линейной комбинацией (т.е. выражается через другие), то вся система векторов является линейно зависимой. Необходимым и достаточным условиями линейной зависимости двух векторов на плоскости (в пространстве R²) является их коллинеарность, а в трёхмерном пространстве (R³) - их компланарность.

Система, состоящая из одного вектора (пространство R¹), будет линейно зависима, если этот вектор нулевой, а если он отличен от нуля – то линейно независима.

В пространстве (на прямой) линейно независимая система не может содержать более одного вектора, т.е. система из двух (и более) векторов всегда линейно зависима.

В пространстве (на плоскости) линейно независимая система не может содержать более двух векторов, т.е. любая система из трёх (и более) векторов линейно зависима.

Если в линейном пространстве имеется линейно независимых векторов, а любыевекторов линейно зависимы, то пространство называется конечномерным, если же линейное пространство таково, что в нём существуют системы сколь угодно большого числа линейно независимых векторов, то это пространство называется бесконечномерным.

Максимально возможное число линейно независимых векторов в конечномерном пространстве называют размерностью этого пространства. Если размерность пространства равна , то его называют- мерным ().

Опр.15. Система линейно независимых векторов в- мерном пространстве называетсябазисом этого пространства.

По векторам базиса можно разложить любой вектор пространства, причём единственным образом.

Разложить вектор по векторам базиса – это представить его в виде линейной комбинации векторов этого базиса.

Если базисом является линейно независимых векторов, то разложение любого векторапо этому базису имеет вид :. (3.4)

Коэффициенты этого разложения, т.е. числа называютсякоординатами вектора в данном базисе.

Для нахождения этих чисел нужно составить систему- линейных уравнений с этими неизвестными, и решить её.

Каждое уравнение составляется по формуле (3.3) из соответствующих координат этих векторов.

П р и м е р Даны векторы: ;;;.

Показать, что векторы образуют базис и разложить векторпо этому базису.

Решение. Векторы образуют базис в трёхмерном пространстве, если они линейно независимы, поэтому нужно составить определитель из координат этих векторов. Если он равен нулю, то его строки (а следовательно и векторы) являются линейно зависимыми, т.е. они не могут образовывать базис, если определитель не равен нулю, то векторы линейно независимы и образуют базис.

Разложить вектор по базису- это значит представить его в виде линейной комбинации этих векторов:

. (*)

Так как вектор получается из векторов базиса по формуле (*), то и каждая его координата получается из соответствующих координат этих векторов по этой же формуле (*).