
- •Глава II. Элементы векторной алгебры и аналитической геометрии
- •§1. Система координат
- •1.1 Система координат на плоскости (пространство r2 )
- •1.2 Простейшие задачи аналитической геометрии Расстояние между двумя точками на плоскости
- •Деление отрезка в данном отношении
- •§2 Векторы.
- •1.Основные понятия
- •2. Линейные операции с векторами Сложение векторов
- •Вычитание
- •Умножение вектора на число
- •3. Проекция вектора на ось
- •4.Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •Обозначим проекции на координатные оси, через.
- •5. Действия над векторами в координатной форме
- •§3. N- мерное векторное пространство. Линейная зависимость и независимость векторов.
- •§4. Скалярное, векторное и смешанное произведения векторов
- •4.1 Скалярное произведение, его свойства и вычисление
- •Механический смысл скалярного произведения
- •Геометрический смысл векторного произведения
- •Механический смысл векторного произведения
- •Свойства векторного произведения
- •Векторное произведение векторов, заданных координатами
- •4.3 Смешанное (векторно-скалярное) произведение векторов, его геометрический смысл
- •Свойства смешанного произведения
- •Смешанное произведение векторов, заданных координатами
Глава II. Элементы векторной алгебры и аналитической геометрии
§1. Система координат
1.1 Система координат на плоскости (пространство r2 )
Декартовая прямоугольная система координат на плоскости считается заданной, если заданы две взаимно перпендикулярные прямые (оси координат), начало отcчёта и единица масштаба.
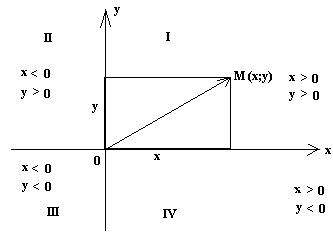 рис.1
рис.1
Горизонтальная ось - ось абсцисс, положительное направление оси - вправо.
Вертикальная ось, перпендикулярная к первой, называется осью ординат. Положительное направление - вверх.
Координаты пишутся в круглых скобках рядом с названием точки, причем на первом месте в прямоугольной системе координат записывается абсцисса точки, а на втором - ее ордината. Например, если x-абсцисса точки, а y - ее ордината, то это записывается так: A(x;y). У точек, лежащих на оси абсцисс, ординаты равны нулю, а у точек, лежащих на оси ординат - абсциссы равны нулю. Абсцисса и ордината точки есть расстояния этой точки до осей ОY и ОХ соответственно, которым приписываются определённые знаки в зависимости от четверти, на которые оси координат делят всю координатную плоскость.
Четверти
(квадранты) и знаки координат указаны
на рисунке 1. Если соединить точку с
началом координат, получим вектор
![]() ,
который называется радиусом - вектором
точки М. Координаты радиуса - вектора
совпадают с координатами точки.
,
который называется радиусом - вектором
точки М. Координаты радиуса - вектора
совпадают с координатами точки.
1.2 Простейшие задачи аналитической геометрии Расстояние между двумя точками на плоскости
Пусть заданы две точки А(х1;y1) и B(x2;y2). Требуется найти расстояние АВ между ними.
По теореме Пифагора: АВ2=АD2+ВD2= =(x2-x1)2+(y2-y1)2 (рис2).
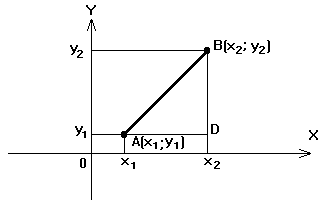 Рис.
2
Рис.
2
АВ=![]() .
(1.1)
.
(1.1)
Расстояние между двумя точками на плоскости равно корню квадратному из суммы квадратов разностей одноимённых координат.
Слагаемые в круглых скобках можно менять местами, т.к. каждая скобка возводится в квадрат.
Деление отрезка в данном отношении
Пусть
А(х1;у1)
и В(х2;у2)
концы отрезка АВ.
Точка С(х;у)
делит отрезок АВ
в отношении
![]() .
.
Требуется найти координаты точки С (рисунок 3).
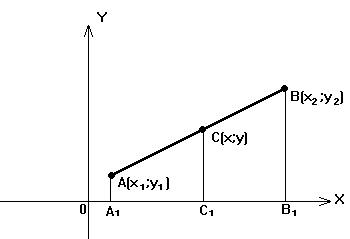 Рис.
3
Рис.
3
Так
как
![]()
( на основе теоремы о пересечении отрезка
параллельными прямыми)
( на основе теоремы о пересечении отрезка
параллельными прямыми) 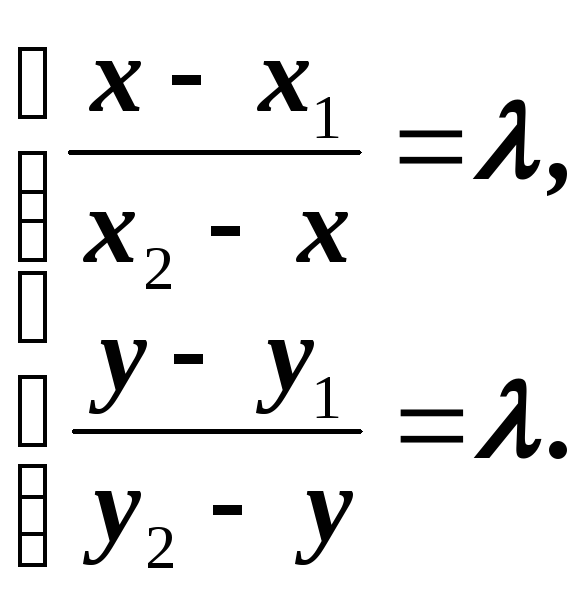 (1.2)
(1.2)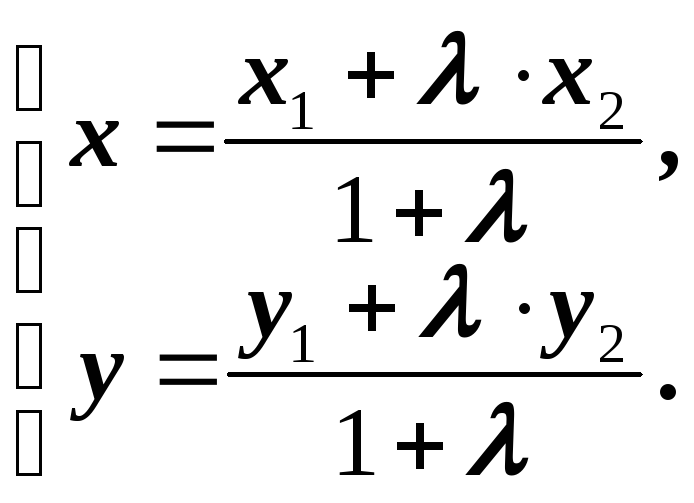 (1.3)
(1.3)
Если
разрешить уравнения (1.2) относительно
Х
и У
получатся формулы (1.3). Если
![]() =1,
то есть точкаС-середина
АВ,
и
=1,
то есть точкаС-середина
АВ,
и
![]() ;
;
![]() (1.4)
(1.4)
Замечание.
Если точка
С
вне отрезка АВ
- за концом отрезка, то
![]() -
отрицательное число (рисунок 4).
-
отрицательное число (рисунок 4).
![]() Рис.
4
Рис.
4
![]() ,
т.к. направление отрезков АС
и СВ
- противоположны
,
т.к. направление отрезков АС
и СВ
- противоположны ![]() .
.
б)
С - за началом отрезка (рисунок 5).![]() и
и![]() .
.
![]() Рис.
5
Рис.
5
§2 Векторы.
Основные понятия.
Линейные операции с векторами
Проекция вектора на ось
Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы.
Действия над векторами в координатной форме.
1.Основные понятия
Опр.1 Величины, которые полностью определяются своими
численными значениями, называются скалярными.
Опр. 2 Вектором называется направленный прямолинейный отрезок.
Обозначается
![]() или
или
![]() .
Вектор считается заданным, если известны
его длина и направление.
.
Вектор считается заданным, если известны
его длина и направление.
Опр.3 Число, равное длине вектора, называется его модулем или длиной вектора.
Обозначается
![]() или
или
![]() .
Модуль может быть только положительным
числом.
.
Модуль может быть только положительным
числом.
Векторы в пространстве свободны, т.е. начало его (точку приложения) можно поместить в любую точку пространства, при этом нужно сохранить длину и направление.
Опр.4 Вектор ВА называется противоположным Вектору АВ.
Опр 5 Вектор называется единичным (е), если длина его равна 1, а если его направление совпадает с направлением данного вектора, то он называется ортом вектора а.
Опр 6 Вектор называется нулевым, если совпадают координаты его
начальной и конечной точек.
Длина нулевого вектора равна нулю.
Опр
7 Векторы
![]() и
и![]() называютсяколлинеарными,
если они лежат
называютсяколлинеарными,
если они лежат
на
одной прямой или на параллельных прямых.
![]()
![]() .
.
Направления их могут быть одинаковыми или противоположными.
Опр.
8 Векторы
![]() и
и![]() называютсяравными,
если они коллинеарные,
называютсяравными,
если они коллинеарные,
имеют
одинаковую длину и направление(![]() ).
).
Опр. 9 Векторы, лежащие в одной плоскости, называются
компланарными.
