Корень n -ой степени из комплексного числа имеет n различных значений, так как, начиная с k = n , корни повторяются.

6.2.Контрольные вопросы

1)Что называется комплексным числом?

2)Геометрическое изображение комплексного числа. Что называется модулем и аргументом комплексного числа?

3)Комплексно-сопряженные комплексные числа. Свойство произведения комплексно-сопряженных чисел.

4)Правила выполнения арифметических действий над комплексными числами в алгебраической форме.

5)Тригонометрическая форма комплексного числа.

6)Формула Эйлера.

7)Показательная форма комплексного числа.

8)Правила арифметических действий над комплексными числами в показательной форме.

6.3.Практическое задание для самостоятельной работы

1.Образуют ли векторы a и b базис на плоскости. Если да, то найти координаты вектора c в этом базисе.

А) a ={3, 1}, b ={−5, 2}, c ={1, −5}.

Б) a ={3, 0}, b ={2, −2}, c ={1, 4}.

В) a ={−1, 2}, b ={3, −4}, c ={2, 7}.

Г) a ={1, 2}, b ={4, 2}, c ={3, 7}.

2. Найти угол между векторами p и q , если p =3a −b , q = 2a − 6b .

А) a ={3 ; 2 ; −4}, b ={−5 ; 0 ; 1},

Б) a ={−2 ; 1 ; −7}, b ={6 ; 5 ; 2},

В) a ={−4 ; 1 ; 7}, b ={3 ; 1 ; 2},

3. Параллелограмм построен на векторах a = p + 3q и b = 2 p −q , где А) p = 4 , q = 6 , ( p,q) = π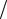6 .

Б) p =5 , q =3 , ( p,q) = π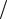4 .

В) p =3 , q = 2, ( p,q) = 2π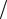3 .

28

Вычислить длину диагоналей этого параллелограмма, угол между диаго-

Б) A(2;4), B(5; 7).

29