
Математический анализ (080500.62, очн., экз)
.pdf
АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ «РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»
КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)
МАТЕМАТИЧЕСКИЙ АНАЛИЗ ТЕСТОВЫЕ ЗАДАНИЯ
Тестовые задания обсуждены на заседании кафедры инженернотехнических дисциплин и сервиса «24» сентября 2012 г. протокол № 2
Заведующий кафедрой |
/А.М. Мухаметшин/ |
СОГЛАСОВАНО
Начальник отдела менеджмента качества |
/Д.Н. Алюшева/ |
1
ПАСПОРТ
№ |
Наименование пункта |
Значение |
1. |
Кафедра |
Инженерно-технические |
|
|
дисциплины и сервис |
2. |
Автор – разработчик |
Поташев А.В., д.ф.-м.н., профессор |
|
|
Поташева Е.В., к.т.н., доцент |
3. |
Наименование дисциплины |
Математический анализ |
|
|
|
4. |
Общая трудоемкость по |
218 (1 семестр) |
|
учебному плану |
|
5. |
Вид контроля (нужное |
Предварительный (входной), |
|
подчеркнуть) |
текущий, промежуточный |
|
|
(экзамен) |
6. |
Для специальности(ей)/ |
080500.62 «Бизнес- |
|
направления(й) подготовки |
информатика» |
|
|
нормативный срок |
|
|
очная форма обучения |
7. |
Количество тестовых заданий |
477 |
|
всего по дисциплине, из них |
|
|
|
|
8. |
Количество заданий при |
26 |
|
тестировании студента |
|
|
|
|
9. |
Из них правильных ответов (в |
|
|
%): |
|
10. |
для оценки «отлично» |
86 % и больше |
|
|
|
11. |
для оценки «хорошо» |
71 % - 85% |
|
|
|
12. |
для оценки |
56% - 70% |
|
«удовлетворительно» |
|
|
или для получения оценки |
- |
|
«зачет» не менее |
|
13. |
Время тестирования (в |
45 |
|
минутах) |
|
2
F1: Математический анализэкзамен1 семестр 2012/2013 F2: Поташев А.В., Поташева Е.В.
F3: Тестовые задания по направлению подготовки 080500.62 «Бизнесинформатика»очнаянормативный срок477 заданий, 26 вопросов
F4: Дидактическая единица; Раздел; Тема V1: Элементы теории пределов
V2: Элементы теории множеств
I:
S: Установить соответствия между списками двух множеств, заданных различным образом:
L1: 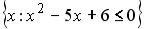
L2: 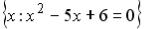
L3: 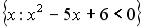
L4: 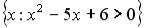 R1:
R1: 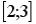
R2: 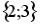
R3: 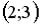
R4: 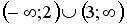
R5: 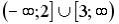
I:
S: Установить соответствия между списками двух множеств, заданных различным образом:
L1: 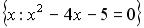
L2: 
L3: 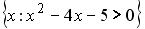
L4: 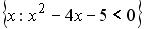 R1:
R1: 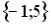
R3: 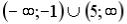
R5: 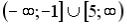
R2: 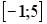
R4: (-1; 5)
I:
S: Установите соответствие между заданными числами и множествами, которым они принадлежат.
L1: 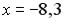
L2: 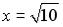 L3:
L3: 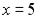
3
L4: 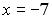
R3: 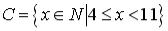
R1: 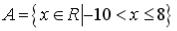
R4: 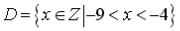
R2: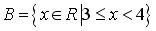 R5: E = { x N |10 ≤ x < 15}
R5: E = { x N |10 ≤ x < 15}
I:
S: Установить соответствия между списками двух множеств, заданных различным образом:
L1: 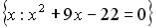
L2: 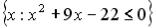
L3: 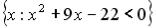
L4: 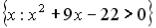 R3:
R3: 
R2: 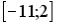
R4: 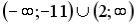
R5: 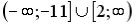
R1: 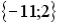
I:
S: Установите соответствие между заданными числами и множествами, которым они принадлежат.
L1: 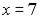
L2: 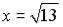
L3: 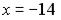
L4: 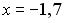
R2: 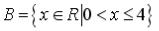
R1: 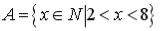 R3:
R3: 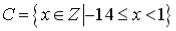
R4: 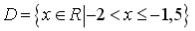
R5: 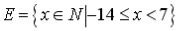
I:
4
S: Мера множества, изображенного на рисунке,
равна…
+:
-:
-:
-:
I:
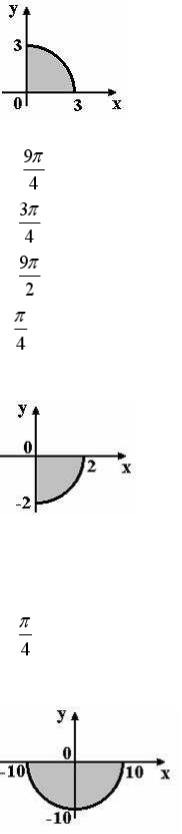
S: Мера множества, изображенного на рисунке,
равна…
-: 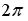 -:
-: 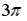
+: 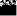
-:
I:
S: Мера множества, изображенного на рисунке,
равна…
-: 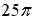 -:
-: 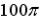 +:
+: 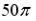
5

-: 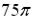
I:
S: Мера множества, изображенного на рисунке,
равна… |
|
|
|
|
|
|
|
|
||
+: |
|
|
|
|
|
|
|
|
|
|
-: |
|
|
|
|
|
|
|
|
|
|
-: |
|
|
|
|
|
|
|
|
|
|
-: |
|
|
|
|
|
|
|
|
|
|
V2: Понятие функции |
||||||||||
I: |
|
|
|
|
|
|
|
2x − 4 |
|
|
S: Областью определения функции ó = |
является множество точек вида |
|||||||||
|
||||||||||
|
|
|
|
|
|
|
|
3x - 2 |
||
|
|
|
|
2 |
||||||
+: |
A = |
x : x ¹ |
|
|
|
|
|
|||
|
|
|
|
|||||||
|
|
|
|
3 |
||||||
|
|
3 |
||||||||
-: |
B = x : x ¹ |
|
|
|
|
|||||
|
|
|||||||||
|
|
2 |
||||||||
|
|
|
2 |
|||||||
-: |
C = |
x : x ³ |
|
|
|
|
||||
|
|
|||||||||
|
|
|
3 |
|||||||
|
|
|
2 |
|||||||
-: |
D = |
x : x £ |
|
|
|
|
||||
|
|
|
||||||||
|
|
|
3 |
|||||||
I: |
= |
|
|
|
|
− |
|
|
|
|
|
|
S: Областью определения функции ó |
x |
− 3 |
|
x + 3 |
является множество |
|||||||
точек вида |
|
|
|
|
|
|
|
|
|
|
|
|
-: A = { x (−∞, −3) [3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
|
-: B = { x [−3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
|
+: C = { x [3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
|
-: D = { x [−3,3]} |
|
|
|
|
|
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
S: Областью определения функции ó |
= |
x |
+ 3 + |
|
|
является множество |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
||||||||
|
|
6 − x |
||||||||||
точек вида
-: A = {x (−∞,−3) [6,∞)} +: B = {x [−3,6)}
6

-: C = { x [−3,6]} -: D = { x (−3,6]} I:
S: Областью определения функции ó = |
9 −x 2 является множество точек |
||||||||||
вида |
|
|
|
|
|
|
|
|
|
|
|
-: A = { x (∞,−3) [3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
-: B = { x (∞, −3] [3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
-: C = { x (−3,3)} |
|
|
|
|
|
|
|
|
|
|
|
+ : D = { x [−3,3]} |
|
|
|
|
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
S: Областью определения функции ó = |
|
|
|
|
|
|
|
|
является множество |
||
x 2 − 4x |
+ 3 |
||||||||||
точек вида |
|
|
|
|
|
|
|
|
|
|
|
-: A = { x [3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
-: B = { x (1,∞)} |
|
|
|
|
|
|
|
|
|
|
|
+ : C = { x (−∞,1] [3,∞} |
|
|
|
|
|
|
|
|
|
|
|
-: D = { x [1,3]} |
|
|
|
|
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
S: Областью определения функции ó = |
|
|
|
|
|
|
|
является множество |
|||
|
5x |
−x 2 − 6 |
|||||||||
точек вида |
|
|
|
|
|
|
|
|
|
|
|
-: A = { x (−∞,2] [3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
-: B = { x (−∞, 2) (3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
-: C = { x (2,3)} |
|
|
|
|
|
|
|
|
|
|
|
+: D = { x [2,3]} |
|
|
|
|
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
S: Областью определения функции ó = log |
|
3 |
|
|
|
|
является множество |
||||
3 |
2x |
− 6 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
точек вида |
|
|
|
|
|
|
|
|
|
|
|
+: A = { x (3,∞)} |
|
|
|
|
|
|
|
|
|
|
|
-: B = { x (−∞,∞)} |
|
|
|
|
|
|
|
|
|
|
|
-: C = { x (−∞,3)} |
|
|
|
|
|
|
|
|
|
|
|
-: D = { x [0,∞)} |
|
|
|
|
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
S: Областью определения функции ó = |
|
|
|
2 |
|
|
|
|
|
является множество |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 − 3x + 2 |
|||||||||
точек вида
+: A = {x (−∞,1) (2,∞)}
7
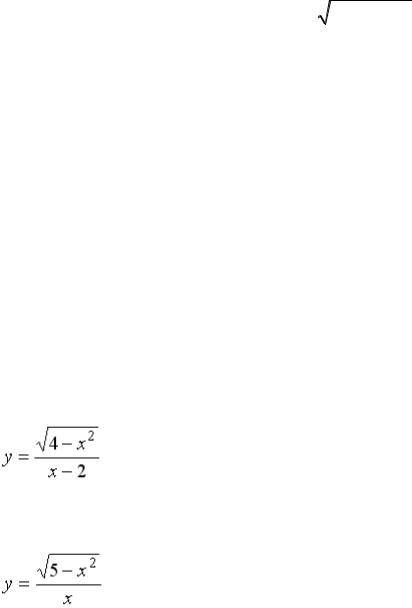
-: B = { x (−∞,1] [2,∞)} -: C = { x (1, 2)}
-: D = { x [0,∞)} I:
S: Областью определения функции ó |
= |
3 |
является множество точек |
|||
x2 − 3x + 2 |
||||||
вида |
|
|
|
|
|
|
-: A ={x : x ¹1} |
|
|
|
|
|
|
-: B ={x Î(-¥,1) È (2,¥)} |
|
|
|
|
|
|
-: C ={x : x ¹ 2} |
|
|
|
|
|
|
+: D ={x : x ¹1, x ¹ 2} |
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
является множество |
|
S: Областью определения функции ó |
= |
|
x2 − 3x + 2 |
|||
|
|
|
|
|||
|
|
|
x − 2 |
|||
точек вида |
|
|
|
|
|
|
-: A ={x Î(-¥,1] È[2,¥)} |
|
|
|
|
|
|
+: B ={x Î(-¥,1] È (2,¥)} |
|
|
|
|
|
|
-: C ={x Î(1, 2)} |
|
|
|
|
|
|
-: D ={x : x ¹ 2} |
|
|
|
|
|
|
I: |
= log (3x −x 2 ) является множество |
|||||
S: Областью определения функции ó |
||||||
5
точек вида
-: A ={x Î(-¥,¥)} -: B ={x Î[0,3]} +: C ={x Î(0,3)} -: D ={x Î(-¥,3]}
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 4
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 4
8
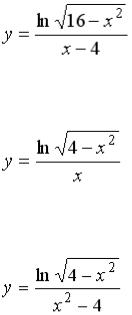
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 7
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 2
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 3
V2: Предел на бесконечности
I:
S:Предел функции lim |
2x5 + 7x3 − 5 |
равен ... |
||||
2x5 − 4x |
||||||
x→∞ |
|
|
|
|
||
+: 1 |
|
|
|
|
|
|
I: |
10x4 + 7x3 − 5x |
|
|
|||
S:Предел функции lim |
|
равен ... |
||||
2x4 − 4x + 1 |
|
|
||||
x→∞ |
|
|
|
|||
+: 5 |
|
|
|
|
|
|
I: |
30x5 + 8x4 − 5x |
|
|
|||
S:Предел функции lim |
|
равен ... |
||||
6x5 + 4x |
|
|
|
|||
x→∞ |
|
|
|
|
||
+: 5 |
|
|
|
|
|
|
I: |
4x5 + 7x3 − 5 |
|
|
|
|
|
S:Предел функции lim |
равен ... |
|||||
2x5 − 4x |
||||||
x→∞ |
|
|
|
|
||
+: 2 |
|
|
|
|
|
|
I: |
3x5 + 8x4 − 5õ |
|
|
|
||
S:Предел функции lim |
равен ... |
|||||
6x5 + 4x |
|
|||||
x→∞ |
|
|
|
|
||
+: 1/2 |
|
|
|
|
|
|
I: |
|
|
|
|
|
|
9

S:Предел функции
+: 3 I:
S:Предел функции
+: 2 I:
S:Предел функции
+: 4 I:
S:Предел функции
+: 2 I:
S:Предел функции
+: -1 I:
S:Предел функции
+: -2 I:
S:Предел функции
+: 3 I:
S:Предел функции
+: 0 I:
S:Предел функции
+: 0 I:
S:Предел функции
+: 0 I:
lim
x→∞
lim
x→∞
lim
x→∞
lim
x→∞
lim
x→∞
lim
x→∞
lim
x→∞
lim
x→∞
lim
x→∞
lim
x→∞
6x4 + x3 − 5 равен ...
2x4 − x
12x4 + 8x3 − 5 равен ...
6x4 + 4x
8x4 + 3x2 − 5 равен ...
2x4 + 4x + 3
4x5 + x3 + 5 равен ...
2x5 − x
x3 + 2x + 5 равен ...
−x3 + 4x
2x7 + 3x − 5 равен ...
−x7 + 4x
−3x7 + 7x5 − 5õ 2 + 3 равен ...
−x7 + 4x
x3 + 8x2 − 5õ равен ...
2x5 + 4x
3x4 + 6x3 − 5x2 равен ...
2x7 − 3x
x6 + 6x3 − 2õ равен ...
3x9 − 4x
10
