14. Понятие динамической системы

Динамическими системами называют класс задач, представленных зада­чами Коши для обыкновенных дифференциальных уравнений (ОДУ) или систем таких уравнений.

Теория динамических систем и специфические численные методы наиболее развиты для динамических систем, описываемых ОДУ (более простые уравнения).

Задача Коши для системысостоит в отыскании неиз-

вестной векторной функции y(t), включающей несколько (L) неизвестных функ­ций, для начального условия у(0) = С.

Соответственно числу компонент векторной функции y(t) должно быть по­ставлено L начальных условий. Исходя из физического смысла такой постановки задачи можно, не теряя общности, полагать, что дифференциальные уравнения содержат производные по аргументу t, являющемуся временем, и, соответственно, описывают динамику во времени различных физических параметров y(t). Поэтому задачи Коши для таких моделей называют динамическими системами, а для их изучения центральным моментом является анализ фазовых портретов, т. е. реше­ний, получающихся при выборе всевозможных начальных условий.

Решения обыкновенных дифференциальных уравнений часто удобнее изо­бражать не в привычном виде, а в фазовом пространстве, по осям ко­торого откладываются значения каждой из найденных функций. При этом аргу­ментtвходит в графики лишь параметрически (см. рис. 1).

В случае двух ОДУ такой график - фазовый портрет системы – является кривой на фазовой плоскости и поэтому особенно нагляден. В общем случае, если система состоит из N ОДУ, фазовое пространство является N-мерным. При N > 3 наглядность теряется, и для визуализации фазового портрета приходится строить его различные проекции. Наиболее просты примеры исключительно линейных уравнений, т. е. содержащих только первую степень неизвестных функций и их производных, как, к примеру, модель линейного гармонического осциллято­ра. Линейные дифференциальные уравнения легко решаются аналитически, а не­обходимость применения численных методов возникает, когда число таких урав­нений в системе ОДУ очень велико. ,

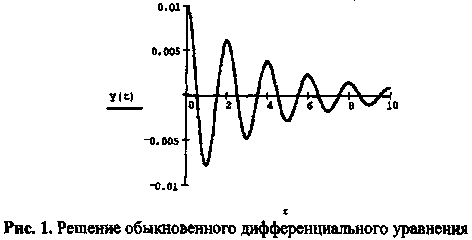
Классические примеры моделей динамических систем, описываемых систе­мами ОДУ: нелинейный осциллятор, динамика популяций (Вольтерра), электрон­ный генератор автоколебаний (Ван дер Поля), турбулентная конвекция жидкости (Лоренца), химическая реакция с диффузией (Пригожина). Все примеры являются типичными динамическими системами и содержат производные по времени t, описывая динамику различных физических параметров.

15. Модели с сосредоточенными и распределенными параметрами

Модели бывают статистическими и логико-математическими, основанными на уравнениях, с той или иной степенью точности описывающих влияние разных факторов на изучаемый объект, явление или процесс. Логико-математические мо­дели делятся на три класса: 1) модели с сосредоточенными параметрами; 2) модели с сосредоточенно-распределенными параметрами, т. е. переходные; 3) модели с распределенными параметрами, основанные на дифференциальных уравнениях в частных производных.

В классе моделей с сосредоточенными параметрами выделяются системные модели типов: а) «черный ящик», т. е. модели типа «вход - выход»; б) системно-физические или концептуальные модели типа «серый ящик», т. е. модели, частич­но учитывающие физику процессов, частично построенные по типу «черного ящика»; в) физические непрерывные модели, т. е. модели, целиком построенные на учете физики явления.

Математическая модель с сосредоточенными параметрами - это модель системы, поведение которой описывается обыкновенными дифференциальными уравнениями.

Данная модель включает в себя переменные, которые зависят только от вре­мени и не зависят от координат. Математическая модель с сосредоточенными па­раметрами имеет вид системы обыкновенных дифференциальных уравнений.

Обыкновенное дифференциальное уравнение (ОДУ) - это дифференци­альное уравнение вида, где x(t) - неизвестная функция (возможно, вектор-функция:в таком случае часто говорят о системе ОДУ), зави­сящая от переменнойt (штрих означает дифференцирование по t). Число n назы­вается порядком дифференциального уравнения.

Решением дифференциального уравнения называется n раз дифференци­руемая функция x(t), удовлетворяющая уравнению во всех точках своей области

определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие, например: потребовать, чтобы решение принимало в данной точке данное значение.

Пример. Одно из простейших применений дифференциальных уравнений -решение нетривиальной задачи нахождения траектории тела по известным проек­циям ускорения. Например, в соответствии со вторым законом Ньютона ускоре­ние тела пропорционально сумме действующих сил; соответствующее дифферен­циальное уравнение имеет видmx=F(x,t). Зная действующие силы (праваячасть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки.

Пример. Дифференциальное уравнение= у (вместе с начальным условиему(0) =1) задает экспоненту: у(х) =. Если х обозначает время, то эта функцияописывает рост популяции в условиях неограниченности ресурсов.

Математическая модель с распределенными параметрами - модель сис­темы, описываемая дифференциальными уравнениями в частных производных.

Модель содержит переменные, зависящие от пространственных координат, и представляет собой систему дифференциальных уравнений в частных производ­ных или систему интегро-дифференциальных уравнений. Важной характери­стикой дифференциальных уравнений является их порядок, т. е. порядок старшей производной, которая входит в эти уравнения.

Пример. Одномерное уравнение теплопроводности, описывающее распро­странение тепла в однородном стержне, имеет вид, где u(t, х) - темпе­ратура, а- положительная константа, описывающая скорость распространения тепла. Задача Коши ставится следующим образом: u(0,x) = f(x), где f(x) - произ­вольная функция.

Пример. Уравнение колебания струны. Данное уравнение имеет вид:

. Здесь u(t, x) - смещение струны из положения равновесия, или из­быточное давление воздуха в трубе, или магнитуда электромагнитного поля в тру­бе, а с - скорость распространения волны. Для того чтобы решить задачу Коши, в начальный момент времени следует задать смещение и скорость струны в началь­ный момент времени:u(0,x) =f(х),

Если модель включает обыкновенные дифференциальные уравнения (кото­рые имеют место в распределенных статических моделях, в динамических моде­лях с сосредоточенными параметрами) или дифференциальные уравнения в част­ных производных (которые имеют место в распределенных динамических моделях с одной или более независимой переменной), то это еще не значит, что поставлен­ная задача решена. Для решения необходимы дополнительные условия: началь­ные - для динамических проблем с производными относительно времени, гранич­ные - для проблем с производными относительно пространственных координат. Дифференциальные уравнения, представляющие собой модель, обычно сводятся кразностным уравнениям, удобным для численного решения на ЭВМ. В этом слу­чае проблема сводится к решению алгебраических уравнений.