
Посібник_MathCad_Лабор
.pdf
Продовження таблиці 11.1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
4 |
|
1 |
|
|
2 |
|
|
3 |
5 |
||
20 |
|
x 2 +e xy |
y(0)=1,6 |
[5,2;6,8] |
0,1 |
||||
21 |
y/ln(y) |
y(2)=1 |
[2;5] |
0,25 |
|||||
22 |
e(x+y)-e(x-y) |
y(0)=0 |
[0;2.5] |
0,1 |
|||||
23 |
1+cos(2x) |
y(π/4)=0 |
[π/4, 3π] |
π/8 |
|||||
|
− 1+sin(( y) |
|
|
|
|||||
|
|
|
|
|
[1;4] |
|
|||
24 |
1 |
1 |
|
y(1)=0 |
0.3 |
||||
|
|
|
|
− |
|
|
|
|
|
|
|
x 2 |
|
y |
|
|
|
||
25 |
sin(3x)-y tg(3x) |
y(0)=1/3 |
[0,4] |
0,25 |
|||||
26 |
cos(x-4y)- |
y(0)=π/4 |
[0,4π] |
π/2 |
|||||
|
cos(x+4y) |
|
[0;3,5] |
|
|||||
27 |
2e-xcos(x)y |
y(0)=0 |
0,1 |
||||||
28 |
e-2ycos(x)+y |
y(0)=0 |
[0;1] |
0,05 |
|||||
29 |
ln x+sin(x) |
y(0)=2,5 |
[1,5;3,5] |
0,2 |
|||||
30 |
ey+2sin(x) |
y(0)=0 |
[0;1,5] |
0,1 |
|||||
|
|
Приклад |
1 |
Знайти розв’язок звичайного диференціального рівняння |
|
|
d |
1 |
|
||
|
|
y(x) =cos(x) + |
|
на інтервалі [0, 100]. Функція має таку початкову умову: |
|
|
dx |
y(x) |
|||
у(0)=1. |
|
|
|||
1.1Ввести ключове слово Given.
1.2Записати, використовуючи логічний знак рівності, наступний вираз:
dxd y(x) = cos( x) + y(1x) .
1.3 Початкову умову записати наступним чином ( використати логічний знак рівності):
у(0)=1.
1.4 Обчислити числовий розв’язок задачі, використовуючи функцію
Odesolve:
у:=Odesolve(t,100).
1.5 Створити цикл t:=0,..10 для визначення точок інтервалу t:=0,..10.
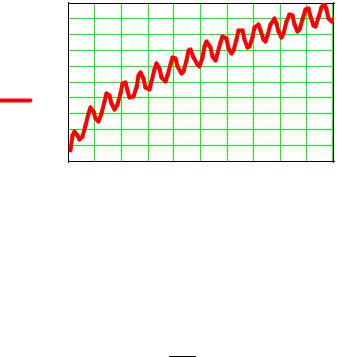
1.6 Побудувати графік функції в точках інтервалу і відформатувати його. Given
dyd y(x) =cos(x) + y(1x) , y(0) =1,
y =Odesolve(x,100),
y(5) = 2.302, y(35) =8.011,
71
|
|
|
|
х:=0..100 |
|
|
|
|
|
||
|
15 |
|
|
|
|
|
|
|
|
|
|
|
13.5 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
10.5 |
|
|
|
|
|
|
|
|
|
|
y ( x) |
9 |
|
|
|
|
|
|
|
|
|
|
7.5 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
4.5 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
0 0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
Рисунок 33 – Графік функції |
|
|
||||||||
Приклад 2 Знайти розв’язок для вище наведеної задачі з використанням вбудованої функції rkfixed.
2.1 Задати початкову умову
у(0):=0.1.
2.2Створити функцію D(x, y) :=cos(x) + y(1x) .
2.3Указати кількість кроків інтегрування К:=100.
2.4Обчислити числовий розв’язок задачі з використанням функції rkfixed. Знак рівності вибивається на панелі Логіка (Булеві).
у=rkfixed(у, х1,х2,К, D).
2.5 Створити цикл х:=0,..100 для визначення точок інтервалу х:=0,..100.
2.6 Побудувати графік функції в точках інтервалу і відформатувати його.
y0 := 0, K := 0, |
|
|
|
D(x, y) := cos(x) + |
1 |
, |
|
y(x) |
|||
|
|
y(x) = rkfixed( y0, x1, x2, K, D).
Примітка. Результати розв’язання диференціального рівняння двома підходами повинні співпасти. Для розв’язання диференціального рівняння можна також використати наступні вбудовані функції: Bulstoer, Rkadapt. Вони мають такі самі параметри як і функція rkfixed, але результати подають з різною точністю:
y(x)  Bulstoer(y0,x1,x2,K,D) , y(x)
Bulstoer(y0,x1,x2,K,D) , y(x)  Rkadapty0(,x1,x2,K,D) .
Rkadapty0(,x1,x2,K,D) .
72
Контрольні питання
1 Які вбудовані функції дозволяють знайти розв’язки звичайних диференціальних рівнянь?
2Чи обов’язково задавати початкові умови для розв’язання звичайних диференціальних рівнянь?
3Як впливає на результат кількість точок розбиття інтервалу інтегрування звичайних диференціальних рівнянь?
Лабораторна робота №12
ПОБУДОВА ТРИВИМІРНИХ ГРАФІКІВ В MATHCAD
Мета роботи – з використанням можливостей MathCad побудувати тривимірні графіки.
Пояснення до виконання лабораторної роботи:
1 Створити графік функції за допомогою панелі Graph (Графічні) з використанням швидкого методу побудови тривимірного графіка (QuickPlot).
2 Відформатувати графік за допомогою вікна 3D-Plot Format або за допомогою команди Format (Формат) контекстного меню.
2.1Змінити тип графіка.
2.2Виконати обертання графіка.
2.3Змінити стиль осей.
2.4Визначити сітку розбиття змінних.
2.5Виконати заливку поверхні функції і її контуру.
2.6Змінити діапазон і крок зміни для х і у.
3 Використати вбудовану функцію для створення тривимірного графіка CreateMesh і відформатувати графік.
4 Порівняти графіки, створені за допомогою швидкого методу побудови тривимірного графіка (QuickPlot) і функції CreateMesh.
Таблиця 12.1 – Варіанти завдання до лабораторної роботи №12
Номер |
Рівняння |
Інтервал |
Кількість точок |
варіанту |
|
побудови графіка |
розбиття на сітці |
1 |
f(x,y)=64-x2-y2 |
x (-8,8); y (0,5) |
kx=40; ky=40 |
2 |
f(x,y)=ln(y2+4x2+8) |
x (-5,5); y (-5,5) |
kx=30; ky=30 |
3 |
f(x,y)= ln(y2+x2)+10 |
x (-3,3); y (-4,4) |
kx=30; ky=30 |
4 |
f(x,y)=xy+x2 |
x (-3,3); y (-7,7) |
kx=30; ky=30 |
5 |
f(x,y)=cos(x+y) |
x (-6,6); y (0,5) |
kx=40; ky=40 |
6 |
f(x,y)=tg(xy-5) |
x (-5,5); y (1,6) |
kx=40; ky=40 |
7 |
f(x,y)=2x(y-y2) |
x (-3,3); y (-2,2) |
kx=20; ky=20 |
8 |
f(x,y)=x3y4 |
x (-5,5); y (-4,5) |
kx=30; ky=30 |
73
Продовження таблиці 12.1
1 |
2 |
|
|
3 |
|
|
4 |
9 |
f(x,y)=x2+sin(y) |
x (-3,3); y (0,5) |
kx=30; ky=30 |
||||
10 |
f(x,y)=xy+sin(y) |
x (-8,8); y (-2,2) |
kx=30; ky=30 |
||||
11 |
f(x,y)=ln(x2+5)+sin(y) |
x (-4,4); y (-3,3) |
kx=40; ky=40 |
||||
12 |
f(x,y)=exy |
x (-5,5); y (-5,5) |
kx=30; ky=30 |
||||
13 |
f(x,y)= ex+y |
x (-3,3); y (-4,4) |
kx=30; ky=30 |
||||
14 |
f(x,y)= e3xcos(y) |
x (-3,3); y (-7,7) |
kx=30; ky=30 |
||||
15 |
f(x,y)= e3xy |
x (-6,6); y (0,5) |
kx=40; ky=40 |
||||
16 |
f(x,y)= eycos(x) |
x (-5,5); y (1,6) |
kx=40; ky=40 |
||||
17 |
f(x,y)= eyx |
x (-3,3); y (-2,2) |
kx=20; ky=20 |
||||
18 |
f(x,y)= eytg(x) |
x (-5,5); y (-4,5) |
kx=30; ky=30 |
||||
19 |
f(x,y)= ey+cos(xy) |
x (-3,3); y (0,5) |
kx=30; ky=30 |
||||
20 |
f(x,y)= ey+sin(x) |
x (-4,4); y (-2,2) |
kx=30; ky=30 |
||||
21 |
f(x,y) =x2+y2-9xy+27 |
x |
|
(0,3); y |
|
(0,3) |
kx=40; ky=40 |
|
|
|
|
|
|||
22 |
f(x,y) = x2+2y2+1 |
x |
|
(0,2); y |
|
(0,1) |
kx=20; ky=20 |
|
|
|
|
|
|||
23 |
f(x,y) =3-2 x2-y2-xy |
x (-3,0); y (0,4) |
kx=30; ky=30 |
||||
24 |
f(x,y) = x2+3y2+x-y |
x |
|
(1,3); y |
|
(1,4) |
kx=30; ky=30 |
|
|
|
|
|
|||
25 |
f(x,y) = 5x2+y2-3xy+4 |
x (-1,0); y (0,1) |
kx=20; ky=20 |
||||
26 |
f(x,y) = 10+9xy-x2 |
x (-5,5); y (1,4) |
kx=40; ky=40 |
||||
27 |
f(x,y) = x2-y2+2xy+4x |
x (-3,3); y (-2,2) |
kx=20; ky=20 |
||||
28 |
f(x,y) = x2+xy-2 |
x (-5,5); y (-4,5) |
kx=30; ky=30 |
||||
29 |
f(x,y) =x2+xy |
x (-1,1); y (0,3) |
kx=20; ky=20 |
||||
30 |
f(x,y) = 3-2x-xy-y2 |
x (-4,4); y (-3,3) |
kx=30; ky=30 |
||||
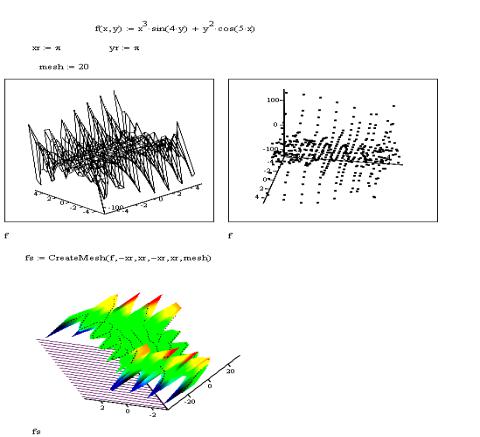
Приклад Створити графік функції f(x,y)=x3sin(4y)+y2cos(5x) на інтервалі длязмінноїх(-π,π) ізмінноїу(-π,π). Крок, зякимзмінюютьсязмінні, дорівнює20.
1 Увести графічну область тривимірного графіка, натиснувши кнопку Surface Plot (Поверхня) панелі Graph (Графічні), або використавши однойменну команду меню Insert (Вставка), або за допомогою поєднання клавіш Ctrl+2.
2 З використанням швидкого методу побудови тривимірного графіка
(QuickPlot) створити графік функції f(x,y)=x3sin(4y)+y2cos(5x).
2.1 Задати вид функції, що визначає тривимірну область, для чого маркер графічної області ввести ім'я заданої функції f, для якої будується тривимірний графік.
3 Відформатувати графік за допомогою вікна 3D-Plot Format або за допомогою команди Format (Формат) контекстного меню
3.1 Змінити орієнтацію графіка, використавши на вкладці General (Загальні) поля Rotation (Обертання), Tilt (Нахил) і Twist (Поворот), тобто визначити відповідні кути обертання, нахилу і повороту (у градусах).
74
3.2Змінити тип графіка, встановивши відповідний перемикач у нижній частині вкладки General (Загальні), наприклад, Data Points і натиснути кнопку ОК.
3.3Змінити стиль заливки ліній для контурного і поверхневого графіків за допомогою вкладки Appearance (Оформлення). Використати при цьому перемикач Fill Surface (Заливка поверхні) із групи Fill Options (Опції заливання)
ігрупу Color Options. Обрати Colormap (Колірна схема) на вкладці Advanced (Додатково).
3.4Змінити параметри настроювання графіка швидкої побудови, які розташовані на вкладці Plot 1 (Графік 1). На цій вкладці змінити параметри сітки розбиття змінних, задавши Start (Початок) –початкову точку побудови прямокутника по даній осі; End (Кінець) – кінцеву точку інтервалу; # of Grids (Кількість ліній сітки) – величину, обернену кроку (кількість ліній сітки).
4 Використати вбудовану функцію для створення тривимірного графіка
CreateMesh (F,-xπ, xπ, -yπ, yπ,mesh), відформатувати графік.
Результат побудови і форматування тривимірного графіка наведено далі.
Рисунок 34 – Тривимірний графік
Контрольні питання
1 Опишіть особливості побудови тривимірних графіків.
2 Як можна зробити обертання графіка?
3 Як можна зробити заливку графіка?
4 Як відформатувати осі на графіку?
5 Як можна змінити діапазон визначити змінних графіка?
75
Лабораторна робота №13
ПОБУДОВА ПРОСТОРОВОЇ ЛІНІЇ І ПАРАМЕТРИЧНО ЗАКРУЧЕНОЇ КРИВОЇ В MATHCAD
Мета роботи – з використанням можливостей MathCad побудувати просторові лінії і параметрично задані криві.
Пояснення до виконання лабораторної роботи:
1 Побудувати просторову лінію:
1.1Створити функцію однієї змінної у вигляді матриці з однієї колонки і трьох рядків (масив даних).
1.2Використати вбудовану функцію CreateSpace, до якої послідовно ввести ім'я масиву даних, початкове і кінцеве значення параметра змінної,
кількість розбивок проміжку параметра. Обрати інтервал зміни змінної (0, 6π) і кількість кроків розбиття 60.
1.3Створити графік функції за допомогою панелі Graph (Графічні) з використанням графіка розсіювання ScatterPlot.
1.4Відформатувати графік за допомогою вікна 3D-Plot Format або за допомогою команди Format (Формат) контекстного меню.
1.4.1 Виконати обертання графіка. 1.4.2 Змінити стиль осей.
1.4.3 Визначити сітку розбиття змінних. 1.4.4 Виконати заливку контуру.
2 Побудувати параметрично задану криву:
2.1Задати рівняння будь-якої функції f(x).
2.2Задати систему параметричного закручування і поєднати її в один
масив:
A(u,v) :=u,
B(u,v):=f(x)cos(v),
C(u,v):=f(x)sin(v),
A(u, v)
M(u,v) := B(u, v) .
C(u, v)
2.3 Унести в маркер наступний запис: CreateMesh(M, s,sl,t,tl,sgrid,tgrid), в
який послідовно занесено ім'я масиву даних, початкові і кінцеві значення параметрів змінних, кількість розбивок проміжку параметрів. Обрати інтервал зміни змінних відповідно (-π, π) і (0, 4π), а також кількість кроків розбиття по кожній змінній 30 і 30.
2.4 Відформатувати графік за допомогою вікна 3D-Plot Format або за допомогою команди Format (Формат) контекстного меню.
76
Таблиця 13.1 – Варіанти завдання до лабораторної роботи №13
Номер |
Функція для створення |
Функція для |
варіанта |
просторової лінії |
параметрично заданої кривої |
1 |
2 |
3 |
1 |
t sin(t) |
f(x)=2cos(x)+5 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
2 |
t +sin(t) |
f(x)=xsin(x) |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
3 |
t −sin(t) |
f(x)= cos(x)+5x |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
4 |
t 2 sin(t) |
f(x)= cos(x)+x2 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
|
|
|
5 |
3t sin(t) |
f(x)=x2cos(x)+1 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
6 |
t +sin(t) |
f(x)= x2sin(x) |
|
|
|
|
t cos(t) |
|
|
F(t)= |
|
|
t |
|
7 |
t sin(t) |
f(x)= xcos(x)+5 |
|
|
|
|
t −cos(t) |
|
|
F(t)= |
|
|
t |
|
8 |
t +sin(t) |
f(x)= x3sin(x) |
|
|
|
|
t cos(t) |
|
|
F(t)= |
|
|
t |
|
9 |
t sin(t) |
f(x)=3x*sin(x2) |
|
|
|
|
cos(t +4) |
|
|
F(t)= |
|
|
t |
|
77
Продовження таблиці 13.1
1 |
2 |
3 |
10 |
(t +3)sin(t) |
f(x)= sin(x+6) |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
11 |
t sin(t) |
f(x)= x+|sin(x) |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
12 |
t sin(t) |
f(x)= cos(x)+5x |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
13 |
t sin(t) |
f(x)= cos(x)+x2 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
14 |
t sin(t) |
f(x)=x2cos(x)+1 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
15 |
t sin(t) |
f(x)=x2cos(x)+1 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
16 |
t sin(t) |
f(x)= x2sin(x) |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
17 |
t sin(t) |
f(x)= xcos(x)+5 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
18 |
t sin(t) |
f(x)= x3sin(x)+1 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
19 |
t sin(t) |
f(x)=3x*sin(x)+x |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
78
Продовження таблиці 13.1 |
|
|
|
|
|
1 |
2 |
3 |
20 |
3t sin(t) |
f(x)= sin(x+6)+x2 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
21 |
t +sin(t) |
f(x)= 7x+|sin(x) |
|
|
|
|
t cos(t) |
|
|
F(t)= |
|
|
t |
|
22 |
t sin(t) |
f(x)=x2cos(x)-1 |
|
|
|
|
t −cos(t) |
|
|
F(t)= |
|
|
t |
|
23 |
t +sin(t) |
f(x)= x2sin(x) |
|
|
|
|
t cos(t) |
|
|
F(t)= |
|
|
t |
|
24 |
t sin(t) |
f(x)= xcos(x) |
|
|
|
|
cos(t +4) |
|
|
F(t)= |
|
|
t |
|
25 |
t sin(t) |
f(x)= xcos(x)-5 |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
26 |
t +sin(t) |
f(x)= x3 -sin(x) |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
27 |
t −sin(t) |
f(x)=3x*sin(x) |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
28 |
t 2 sin(t) |
f(x)= sin(x-6) |
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
|
|
|
79
Продовження таблиці 13.1
1 |
2 |
3 |
29 |
3t sin(t) |
|
|
|
|
|
cos(t) |
|
|
F(t)= |
|
|
t |
|
30 |
t sin(t) |
f(x)= x-|sin(x) |
|
|
|
|
cos(t +4) |
|
|
F(t)= |
|
|
t |
|
Приклад 1 Побудувати просторову лінію.
1.1Створити функцію однієї змінної t у вигляді матриці з однієї колонки
ітрьох рядків (масив даних):
sin (t) t
|
|
|
|
F(t) := |
cos (t) t . |
||
|
|
t |
|
1.2 Використати вбудовану функцію CreateSpace, до якої послідовно ввести ім'я масиву даних, початкове і кінцеве значення параметра змінної, кількість розбивок проміжку параметра:
fp := CreateSpace(F,0,6π,80).
1.3Створити графік функції за допомогою панелі Graph (Графічні) з використанням графіка розсіювання ScatterPlot.
1.4Відформатувати графік за допомогою вікна 3D-Plot Format або за допомогою команди Format (Формат) контекстного меню.
1.4.1 Виконати обертання графіка. 1.4.2 Змінити стиль осей.
1.4.3 Визначити сітку розбиття змінних. 1.4.4 Виконати заливку контуру. Результат побудови графіка наведено нижче.
sin(t) t F(t) := cos(t) t
t
fp := CreateSpace (F,0,6 π,80)
80
