Посібник_MathCad_Лабор

3.2 Тривимірні графіки

Для побудови тривимірних графіків можна використовувати найбільш простий і практично важливий, швидкий метод побудови тривимірного графіка (QuickPlot). У його основі лежить той самий принцип, що й при швидкому заданні двовимірної залежності: користувач визначає тільки вид функції, а всі параметри побудови, такі як крок між вузловими точками, діапазон шкал осей і система координат задаються автоматично системою.

Типи тривимірних графіків наступні:

•Contour Plot - графік ліній рівня (графік поверхні);

•3D Bar Plot - графік тривимірної гістограми);

•3D Scatter Plot - графік множини точок;

•Vector Field Plot - графік векторного поля.

Графік векторного поля трохи відрізняється від інших типів двовимірних графіків. Його зміст полягає в побудові деякого вектора в кожній точці площини XY. Щоб задати вектор на площині, потрібні два скалярних числа. Тому в MathСad прийнято, що векторне поле задає комплексна матриця. Дійсні частини кожного її елемента задають проекцію вектора на вісь х, а мнимі — на вісь Y.

Щоб створити тривимірний графік, потрібно натиснути кнопку з зображенням кожного з типів тривимірних графіків на панелі інструментів Graph (Графіки). У результаті з'явиться порожня область графіка з трьома осями (рис. 4) і єдиним заповнювачем у нижньому лівому куті. У цей заповнювач або ім'я z функції z(x,y) двох змінних для швидкої побудови тривимірного графіка або імені матричної змінної z, що задає функцію z(x,y) на площині XY.

Рисунок 4 – Область для створення тривимірних графіків

3.2.1 Спосіб побудови з використанням швидкого методу побудови тривимірного графіка

Послідовність створення тривимірного графіка з використанням швидкого методу побудови тривимірного графіка (QuickPlot) наступна.

1 Спочатку треба ввести графічну область тривимірного графіка. Аналогічно залежності X-Y, це можна виконати трьома стандартними

11

способами: або натиснувши кнопку Surface Plot (Поверхня) панелі Graph (Графічні), або використавши однойменну команду меню Insert (Вставка), або за допомогою поєднання клавіш Ctrl+2.

Для побудови тривимірних графіків існує тільки один маркер заповнення. У загальному випадку в ньому повинний бути прописаний масив, що містить координати вузлових точок по всім трьох осях.

2 Після того як графічна область введена, слід задати вигляд функції, що визначає тривимірну область. На відміну від X-Y-залежностей, просто ввести функцію в маркер не можна – при цьому буде видане повідомлення про помилку: This variable is undefined (Дана змінна не визначена). У маркер графічної області вводиться ім'я заданої функції, для якої будується тривимірний графік. Однак на відміну від двовимірного випадку, прописаним повинен бути лише безпосередньо текст імені, без змінних у дужках.

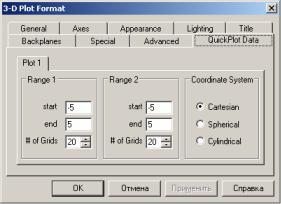
Під час використання даної методики поверхня задається на стандартному інтервалі від -5 до 5 для – змінних. Такий діапазон у багатьох випадках може бути неприйнятний. Для форматування параметрів графіків швидкої побудови існує спеціальна вкладка Quick Plot Data (дані графіка швидкої побудови) вікна форматування тривимірних графіків 3D-Plot Format. Відкривається це вікно або подвійним натисканням лівою кнопкою миші на графічній області, або за допомогою команди Format (Формат) її контекстного меню (рис. 5).

Усі параметри настройки графіка швидкої побудови розташовані на вкладці Plot 1 (Графік 1). У загальному випадку таких вкладок може бути більше, що пов'язано з тим, що на одній графічній області може бути розміщено кілька поверхонь. Для виконання цієї дії вводяться через кому імена функцій, графіки яких повинні бути побудовані. Вкладка Plot 1 (Графік 1) містить три меню настроювання, два з яких: Range 1 і Range 2 (Ряд 1 і Ряд 2) є ідентичні один одному. Ці меню відповідають за характеристики сітки побудови поверхні уздовж кожної з осей змінних (відповідність змінної ряду визначається послідовністю введення її під час задання імені функції) і містять наступні параметри настроювання:

–Start (Початок). У полі даного параметру можна довільним чином задати початкову точку побудови прямокутника по даній осі;

–End (Кінець). У полі даного параметру визначається кінцева точка інтервалу;

–# of Grids (Кількість ліній сітки). Параметр визначає, на скільки відрізків буде розбитий інтервал побудови за обраною змінною (що відповідає числу відображених ліній сітки). Ця величина зворотна до кроку зміни змінної.

Аналогічно двовимірному випадку, інтервал по кожній з осей змінних розбивається на задану кількість відрізків. Границі цих відрізків дають координати вузлових точок. При цьому, якщо кількість відрізків по X дорівнює N, а по Y – М, то для кожного значення X буде існувати М точок з різними координатами по Y, і, навпаки, кожному Y буде відповідати N значень X. Візуально це можна представити у вигляді сітки, яка визначається кроком

12

відносно кожної із змінних, а у вузлах знаходяться точки, щодо яких визначається функція.

Коли сітка розбиття задана, обчислюються значення функції в її вузлах. Якщо зупинитися на цьому етапі і візуалізувати тільки точки, то буде побудований так званий точковий графік (Data Points). Кожна точка з'єднується із сусідніми за допомогою відрізків прямих, при цьому застосовуються згладжування й інші графічні ефекти, у результаті чого, залежно від величини кроків сітки, виходить більш-менш гладка поверхня.

Рисунок 5 – Вікно для форматування тривимірних графіків

Третє меню вкладки Plot 1 (Графік 1) — Coordinate System (Система координат) визначає, у якій системі координат слід відобразити дану залежність. Можливі наступні варіанти:

•Cartesian (Декартова). Графік відображається в декартовій системі координат.

•Spherical (Сферична). Графік відображається в сферичній системі координат.

•Cylindrical (Циліндрична). Графік відображається в циліндричній системі координат.

У діалозі 3-D Plot Format (Форматування 3-D графіка) доступна значна кількість параметрів, зміна яких здатна вплинути на зовнішній вигляд графіка. Вони згруповані за принципом дії на декількох вкладках.

Зупинимося коротко на можливостях оформлення тривимірних графіків. Зміна типу графіка Щоб змінити тип уже наявного графіка (наприклад побудувати замість поверхні графік ліній рівня і т.д.), треба встановити відповідний перемикач у нижній частині вкладки General (Загальні) і натиснути

кнопку ОК. Графік буде перетворений (рис.6).

Обертання графіка Найпростіший спосіб орієнтації системи координат із графіком у тривимірному просторі – це перетягування її покажчиком миші. Можна переміщати при натиснутій лівій кнопці миші покажчик у межах

графіка, після чого буде видно, як повертається графік.

Зміна орієнтації графіка За допомогою полів Rotation (Обертання), Tilt (Нахил) і Twist (Поворот) на вкладці General (Загальні) визначають відповідні

13

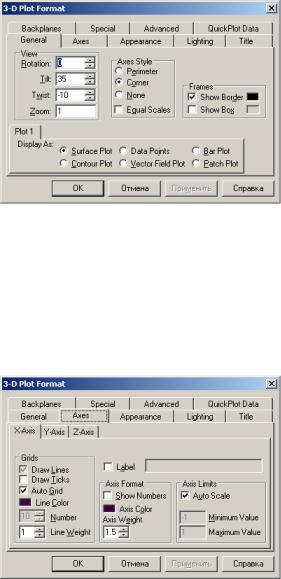
кути обертання, нахилу і повороту (у градусах) і тим самим задають напрямок усіх трьох осей координат у просторі.

Стиль осей можна змінити за допомогою групи перемикачів Axes Style (Стиль осей) і задати один з наступних стилів осей координат:

•Perimeter (Периметр);

•Corner (Кутом);

•None (Немає) – осі відсутні.

Якщо встановити прапорець Show Box (Показати куб), то координатний простір буде зображено у вигляді куба.

Масштабуванням графіка можна задати числове значення масштабу у полі Zoom (Масштаб) вкладки General (Загальні).

Рисунок 6 – Вкладка General (Display as) для зміни типу графіка

Форматування осей відбувається з використанням вкладки Axes (Осі) (рис. 7). Вкладка Axes (Осі) містить три вкладених вкладки, в яких задаються параметри для кожної з трьох координатних осей. Зокрема, можна включити або відключити показ ліній сітки, нумерації і задати діапазон по кожній із осей.

Рисунок 7 – Вкладка Axes (Осі) форматування осей

За допомогою ще однієї вкладки — Backplanes (Площини заднього плану) (рис. 8) задається показ проекцій координатної сітки на три сховані площини тривимірного графіка.

14

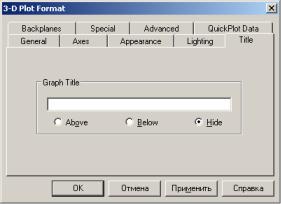
Заголовок графіка можна змінити за допомогою вкладки Title (Заголовок) (рис. 11).

Рисунок 11 – Вкладка TITLE для зміни заголовка графіка

3.2.2 Спосіб побудови тривимірного графіка за допомогою матриці

Існує ще один спосіб побудови тривимірного графіка за допомогою матриці значень, яка являє собою таблицю із трьох колонок: у першій будуть розташовані координати точок по вісі X, у другій – по вісі Y, у третій – по вісі Z. У MathСad існує спеціальна функція маtrіх(m,n,f) (матриця). Функція формує матрицю, елементи якої дорівнюють значенням функції f(x,y), виходячи з тієї умови, що x=і, y=j (тобто змінні визначаються рівними відповідним матричним індексам даного елемента). Кількість рядків створюваної матриці визначається в першому маркері імені функції (параметр m) , кількість колонок – у другому (параметр n).

Аналогічно двовимірному випадкові, задати поверхню можна, використовуючи оператор ранжированої змінної за готовими матрицями.

3.2.3 Спосіб побудови за допомогою спеціальної матричної функції CreateMesh

Можна створити графік за допомогою спеціальної матричної функції

CreateMesh (Створити сітку). Функція CreateMesh(F,s,sl,t,tl,sgrid,tgrid,fmap)

вводиться у маркер графічної області і має порожні маркери, в яку послідовно вводяться:

•ім'я матриці значень або функції F;

•початкове значення першої змінної s;

•початкове значення другої змінної sl;

•кінцеве значення першої змінної t;

•кінцеве значення другої змінної tl;

•число ліній сітки відносно першої змінної sgrid;

•кількість ліній сітки відносно другої змінної tgrid;

•карта відображення frnap.

16

Крім поверхонь у просторі можна задавати і різного роду лінії. Для цього існує спеціальна функція CreateSpace(F,t,tl,tgrid,frnap) (Створити просторові). Вона має п'ять маркерів, у які послідовно вводиться ім'я масиву даних або системи параметричних рівнянь, початкове і кінцеве значення параметра, кількість розбивок проміжку параметра, карта відображення.

Параметричне закручування дозволяє створювати графіки, які задані в параметричній формі. Послідовність дій з використанням алгоритму параметричного закручування є наступною.

1Задати рівняння будь-якої функції f(x).

2Задатисистемупараметричногозакручуванняіпоєднатиїїводин масив:

A(u,v) :=u,

B(u,v):=f(u)cos(v),

C(u,v):=f(u)sin(v),

A(u, v)

M(u,v) := B(u, v) .

C(u, v)

3 Занести в маркер наступний запис: CreateMesh(M, s,sl,t,tl,sgrid,tgrid).

4 СИМВОЛЬНІ ОБЧИСЛЕННЯ

Під час аналітичних обчислень результат представляється в нечисловій формі в результаті тотожних перетворень, найпростішими серед яких є розкриття дужок.

За допомогою символьного процесора MathCad можна розв’язувати інженерні задачі в аналітичному вигляді і проводити широкий спектр аналітичних перетворень, таких як: спрощення виразів і алгебраїчні перетворення, алгебраїчні і матричні операції, основні дії математичного аналізу тощо.

Розкладання алгебраїчного виразу – це математичне перетворення, яке переводить ступені і добутки в більш прості співвідношення. При розкладанні тригонометричних виразів функції кратного аргументу перетворюються в

загального знаменника, виносити множник за дужки, розкладати на елементарні дроби, виконувати підстановки і заміни у змінних.

Символьні обчислення можна виконувати таким чином:

–за допомогою команд меню;

–за допомогою оператора символьного виведення →,

–ключових слів символьного процесора;

–звичайних формул.

Для символьних обчислень за допомогою команд призначено головне меню Symbolic (Символіка), яке об’єднує математичні операції. Для реалізації другого підходу застосовуються всі засоби MathCad (наприклад, Calculator, Evaluation, тощо).

17

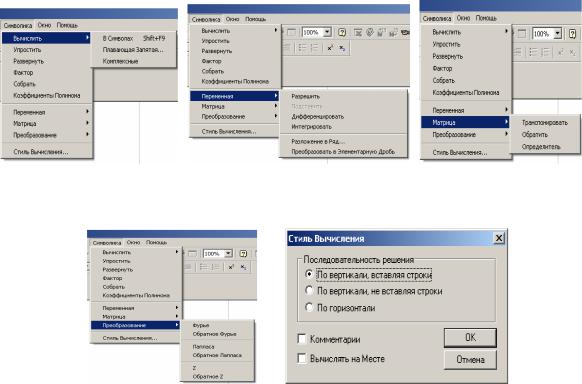
За допомогою меню Symbolic (Символіка) можна виконувати такі операції:

•Symbolic/Evaluate (Символіка/Обчислення ) символьне обчислення, в

тому числі із плаваючою точкою (рис.12,а);

•Symbolic/Simplify (Символіка/Спрощеннявиразів) спрощеннявиразів;

•Symbolic/Expand (Символіка/Розкладання виразів) розкладання виразів на елементарні;

•Symbolic/Factor(Символіка/Розкладання на множники) розкладання на множники;

•Symbolic/Collect(Символіка/Подібні) приведення подібних;

•Symbolic/Polynomial Coefficients (Символіка/Поліноміальні коефіцієнти)

визначеннякоефіцієнтів поліномів;

•Symbolic/Variable(Символіка/Змінна/…) розв’язання рівняння; підстановка змінних ; диференціювання; інтегрування; розкладання в ряди; розкладання на елементарнідроби(рис.12,б));

•Symbolic/Matrix(Символіка/Матриці) дії з матрицями (рис.12,в);

•Symboliс/Transform(Символіка/Інтегральні перетворення) перетворення Фур’є, Лапласа) (рис.12,г).

Послідовність виконання обчислень можна задати з використанням Стиля Вычислений (рис.12, д).

г) д)

Рисунок 12 – Команди меню Symbolic

18

5 ДІЇ З МАТРИЦЯМИ

Для матриць визначені наступні операції: додавання, добуток, обернення, транспонування, тощо. За допомогою вбудованих функцій MathCad матриці можна об’єднувати; виділяти в них під масиви; визначати розміри масивів; максимальні, мінімальні значення; знаходити власні числа і вектори.

Для створення матриць потрібно записати оператор присвоювання, для введення правої частини використати команду Insert/Matrix або команду Matrix на панелі інструментів. У вікні, що розкриється, задаються числа рядків і колонок матриці. Вектор є матрицею з однією колонкою. Значення елементів матриці потрібно ввести у відповідні місця. Далі можна виконувати всі необхідні операції з матрицями (рис. 13).

Рисунок 13 – Діалогове вікно для визначення розміру матриці

Для роботи з елементами матриці використовуються індекси елементів. Нумерація рядків і колонок матриці починається з нуля. Індекс елемента визначається на панелі інструментів Matrix за допомогою кнопки Subscript (рис.2,в), наприклад Mn,k. Два індекси, що визначають елемент матриці, відділяються комою. Номер колонки матриці відображається як верхній індекс, що взятий у кутові дужки, для чого використовується кнопка Column на панелі інструментів Matrix, наприклад, М<1> .

Для проведення операцій з матрицями використовується меню Symbolic і

команда Matrix (рис. 14).

Рисунок 14 – Меню Symbolic для роботи з матрицями в символьному вигляді

19

6ЗНАХОДЖЕННЯ КОРЕНІВ РІВНЯННЯ, РОЗВ’ЯЗОК РІВНЯНЬ

ІСИСТЕМ РІВНЯНЬ

Для чисельного пошуку коренів рівняння в MathCad використовується вбудована функція root. Вона дозволяє розв’язувати рівняння вигляду f(x)=0, де f(x)–рівняння корені якого треба знайти, х – невідоме. Використання функції root потребує задання початкового наближення.

Функція polyroot повертає вектор, що має всі корені рівняння, коефіцієнти якого задаються вектором v. Коефіцієнти вектора v

розв’язання заключається в визначенні за графіком функції, що відповідає лівій частині рівняння, за якою величина аргументу даної функція набуває значення, рівного правій частині рівняння.

Усі методи розв’язання систем лінійних алгебраїчних рівнянь можна розділити на дві основні групи: прямі (метод Крамера, метод Гауса тощо) і ітеративні методи. Використовуючи прямі методи, розрахунки можна вести як чисельно, так і символьно. Ітеративні методи застосовуються в чисельних розрахунках.

Для розв’язання систем лінійних і нелінійних рівнянь використовується «блок рішень», який починається з ключового слова given і закінчується викликом функції find. Між ними знаходяться рівняння. Всім невідомим у рівнянні повинні надаватися початкові значення. В рівнянні, для якого необхідно знайти рішення, потрібно використовувати знак логічної рівності = на панелі інструментів Evaluation. Аргументами функції повинні бути невідомі, які необхідно знайти.

Розв’язок системи лінійних рівнянь за допомогою вбудованої функції lsolve(А,b) повертає вектор розв’язків b. Матриця А – квадратна невироджена, вектор b – вектор правих частин в системі рівнянь.

За допомогою символьного процесора MathCad можна отримувати аналітичні розв’язки системи рівнянь, використовуючи оператор solve. В цьому випадку система повинна бути занесена в лівий маркер оператора у вигляді вектора. Змінні, значення яких обчислюються, слід вводити через кому в правий маркер оператора solve. Відповідь буде представлено у вигляді матриці, в рядках якої будуть записані знайдені значення невідомих системи рівнянь.

Аналітичні розв’язки можна також одержати за допомогою «блоку розв’язань», який починається з ключового слова given.

Наближені розв’язки системи рівнянь можна одержати з використанням вбудованої функції minerr( x1,…). Ця функція подібна за своєю роботою до функції find, але вона має інші умови для завершення ітеративного процесу знаходження роз’язків. Функція minerr дозволяє знаходити розв’язки в тому випадку, коли їх не знаходить функція find.

20