Посібник_MathCad_Лабор

7 ОБЧИСЛЕННЯ ПОХІДНИХ І ІНТЕГРАЛІВ

Аналогічно більшості інших найбільш важливих математичних операцій, у MathCad існує чисельне і символьне диференціювання. Символьний метод має переваги в тому плані, що результат можна одержати у вигляді функції, яку можна буде використовувати в подальших розрахунках. Чисельний же підхід має переваги в деяких специфічних задачах. MathCad дозволяє обчислювати як звичайну похідну, так і похідні більш високих порядків, а також часткові похідні (рис. 15).

Оператор простого диференціювання на панелі Calculus для обчислення першої похідної має два маркери, принцип заповнення яких такий: у верхній вводиться функція, у нижній – змінна, за якою обчислюється похідна.

Рисунок 15 – Діалогове вікно для обчислення похідних і інтегралів

Результат може бути представлено в символьному вигляді, якщо використати оператор символьного виведення →, а потім звернутися до символьного процесора Symbolic/Evaluate (Символіка/Обрахувати в символах) (рис. 16).

Рисунок 16 –Меню символьного процесора Symbolic для обчислення в символах

Під час символьного диференціювання можна оперувати з функціями декількох змінних. Оператор диференціювання може поєднуватися з будь-яким обчислювальним або символьним оператором. Особливо корисним є оператор Simplify, так як вираз похідної подається в неспрощеному видгляі. Для спрощення відповіді варто використовувати оператори Collect (наводити подібні), Factor (розкладає вирази на множники) і Expand (розкриває дужки).

Щоб одержати числове значення похідної в потрібній точці, виходячи з результатів символьного розрахунку, потрібно виконати наступні дії:

21

1 Знайти функцію похідної, використовуючи оператор символьного виведення (→).

2Присвоїти змінній відповідне числове значення.

3Скопіювати одержаний вираз для похідної й обчислити його символьно.

Панель Calculus (Обчислення) містить два оператори інтегрування. Перший, Indefinite Integral (Невизначений інтеграл), дозволяє визначити вигляд функції, що інтегрується (рис. 15). Оператор невизначеного інтеграла містить два маркери, що заповнюються цілком відповідно до прийнятого в математиці подання: у лівий маркер вводиться функція (або ім'я функції), під знак диференціала – змінна інтегрування.

Найчастіше результат інтегрування являє собою громіздкий вираз. У цьому випадку його варто спрощувати. Найбільш універсальним інструментом, який для цього використовується, є оператор Simplify (Спростити). Однак іноді вираз можна спростити (оператор Collect), розклавши на ступені (оператор Expand) або знайти в дробі загальний знаменник (оператор Factor). Щоб задіяти потрібний символьний оператор, варто виділити вираз інтеграла і натиснути відповідну кнопку на панелі Symbolic (Символьні). До результату інтегрування можна застосувати відразу кілька символьних операторів.

Знаходження визначеного інтеграла виконується подібно тому, як обчислюється невизначений інтеграл. Для інтегрування необхідно звернутися на панелі Симольні до функції simplify, ввести оператор інтегрування. У відповідні місця занести ім’я першої змінної і границі інтегрування. Якщо необхідно обчислити кратні інтеграли, то на місці введення функції під інтегралом ввести ще один оператор інтегрування, границі інтегрування і підінтегральну функцію. Аналогічно виконується інтегрування відносно декількох змінних.

Можна визначити інтеграл у символьному вигляді, наприклад,

Для чисельного інтегрування MathCad пропонує скористатися вбудованими програмами обчислення інтегралів (рис. 17). Для того, щоб звернутися до наближеного розрахунку, треба в контекстному меню обрати один із методів інтегрування.

Рисунок 17 –Меню із вбудованими програмами для чисельного інтегрування

22

8 ОБЧИСЛЕННЯ ЗВИЧАЙНИХ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ

Диференційні рівняння – це рівняння, в яких невідомими є функції однієї або декількох змінних. Ці рівняння мають співвідношення між функціями, які належить знайти, і їх похідними. Якщо в рівнянні присутні похідні відносно однієї змінної, то вони є звичайними диференціальними рівняннями (ОДУ).Знайти розв’язок диференціального рівняння (або проінтегрувати його)

– це значить визначити невідому функцію на заданому інтервалі зміни її змінних. Диференційне рівняння має один розв’язок, разом з рівнянням задано початкові умови.

За допомогою MathCad можна знайти розв’язок задач Коші, для яких задано початкові умови, на функції, яку необхідно знайти, тобто задані значення цієї функції знаходяться в початковій точці інтервалу інтегрування рівняння. В більшості випадків диференційне рівняння першого порядку можна записати в стандартній формі (формі Коші):

і тільки з такою формою рівняння може працювати обчислювальний процесор MathCad . Разом з рівнянням (1) необхідно задати початкові умови – значення функції у(t0) в деякій точці t0. Таким чином, необхідно знайти функцію у(t) на інтервалі [t0, t].

Для чисельного інтегрування в MathCad є можливість використовувати блок Given/Odesolve або вбудовані функції.

Обчислювальний блок Given/Odesolve, який реалізує розв’язок одного звичайного диференціального рівняння методом Рунге –Кутта, скадається з трьох частин:

1)ключове слово Given;

2)диференційне рівняння і початкова умова, які записані за допомогою логічних операторів, причому початкова умова повинна записуватися у формі у(t0)=b;

3)Odesolve(t,t1) – вбудована функція для розв’язання ОДУ відносно

змінної t на інтервалі [t0, t].

Для розв’язання ОДУ можна використовувати також вбудовані функції rkfixed, Pkadapt, Bestoer.

9 ПРОГРАМУВАННЯ В MATHCAD

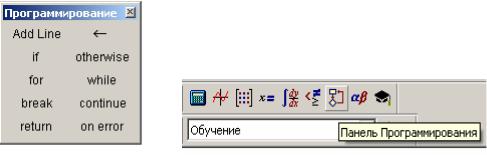
Для написання програм у середовищі MathCad [4,6] існує спеціальна панель Programming (Програмування) (рис.18, а), вона відноситься до панелі Math (Математичні) (рис.18, б).

Мова програмування MathCad має гранично малу кількість операторів (рис. 18,а). Щоб написати програму, насамперед для неї повинен бути створений блок. Виглядає він як чорна вертикальна лінія з маркерами, у які заносяться ті або інші вирази алгоритму.

23

оператор майже завжди працює з оператором if (Якщо) або on error (Перехват помилок).

Програмний оператор умови if (Якщо) використовується практично в усіх створюваних алгоритмах. Умовний оператор if має два маркери: • if •. У правий маркер вводиться умова, у лівий – операція, яка спрацює у випадку, якщо умова виконується (якщо ж вона не виконується, то програма, пропускає даний фрагмент). В маркер оператора може бути внесено кілька умов.

Якщо алгоритм має декілька умов, при цьому виконання однієї з них може привести до невиконання або помилки в інших операторах умов, то можна використати спеціальний оператор continue (Продовжити). Його застосування аналогічно застосуванню оператора break (Перервати).

Оператор otherwise (Інакше) призначено для визначення дії, яка повинна бути виконана, якщо умова оператора if (Якщо) виявиться неістинною. Одночасно може бути використано кілька умовних операторів if (Якщо). Оператор otherwise (Інакше) у такому випадку буде задіяний, якщо не виконаються умови всіх операторів if (Якщо).

За допомогою оператора return (Повернути) можна перервати роботу програми і повернути деяке значення. Цей оператор використовується у разі помилкової ситуації в програмі.

У MathCad існує можливість використовувати спеціальний оператор on error (Перехват помилок). Він дає можливість уникати у програмах помилок і обходити їх. Цей оператор за своїм синтаксисом повністю відповідає оператору if.

10 ОБРОБКА ДАНИХ ЗАСОБАМИ MATHCAD

Відомо, що експериментальні дані, як правило, задаються дискретно у вигляді масиву даних із двох пар чисел (хi, уi). У зв’язку з цим виникає завдання апроксимації дискретних даних неперервною функцією f(x). В MathCad для обробки експериментальних даних існують вбудовані функції, які дозволяють виконувати інтерполяцію.

Для побудови лінійної інтерполяції служить вбудована функція linterp. linterp(x,y, t) – функція, що апроксимує дані векторів х і у кусково-

лінійною залежністю;

• х – вектор дійсних даних аргументу;

• у – вектор дійсних даних значень того розміру;

• t – значення аргументу, при якому обчислюється інтерполяційна функція.

Зауваження. Елементи вектора х повинні бути визначені в порядку зростання.

Щоб здійснити лінійну інтерполяцію, треба виконати наступні дії: 1 Ввести вектори даних х і у

2 Визначити функцію linterp (х,у, t ) .

3 Обчислити значення цієї функції в необхідних точках (наприклад, linterp(x,y,2,4) =3,52 або linterp(х,у,6) =5.9) або побудувати її графік.

25

Зауваження. Функція A ( t ) на графіку має аргумент t, а не х. Це означає, що функція A ( t ) обчислюється не тільки при заданих значеннях аргументу, а й при набагато більшому числі аргументів у інтервалі зміни змінної, що автоматично забезпечує MathСad. MathСad, за умовчанням, з'єднує точки графіка прямими лініями, здійснює їхню лінійну інтерполяцію.

У більшості практичних додатків бажано з'єднати экспериментальні точки не ламаною лінією, а гладенькою кривою. Найкраще для цих цілей підходить інтерполяція кубічними сплайнами, тобто відрізками кубічних парабол.

Функція interp(s,x,y,t) апроксимує дані векторів х і у кубічними сплайнами і має такі аргументи:

•s – вектор других похідних, створений однією з функцій cspline, pspline

або lspline;

•х – вектор дійсних даних аргументу, елементи якого розташовані в порядку зростання;

•у – вектор дійсних даних значень того самого розміру;

•t – значення аргументу, при якому обчислюється функція, що інтерполюється.

Перед застосуванням функції interp необхідно попередньо визначити перший з її аргументів – векторну змінну s. Виконується це за допомогою однієї з трьох вбудованих функцій тих же аргументів (х,у):

•ispiine(x,y) — вектор значень коефіцієнтів лінійного сплайна;

•pspiine(x,y) — вектор значень коефіцієнтів квадратичного сплайна;

•cspline(x,y) — вектор значень коефіцієнтів кубічного сплайна;

•х,у — вектори даних.

Більш складний тип інтерполяції – так звана інтерполяція В-сплайнами. На відміну від звичайної сплайн-інтерполяції, зшивання елементарних В- сплайнов виконується не в точках х і у, а в інших точках, координати яких пропонується ввести користувачеві. Сплайни можуть бути поліномами 1, 2 або 3 ступеня (лінійні, квадратичні або кубічні). Застосовується інтерполяція В- сплайнами так само, як і звичайна сплайн-інтерполяція, розходження виявляється тільки у визначенні допоміжної функції коефіцієнтів сплайна.

Лабораторна робота №1

УВЕДЕННЯ ФОРМУЛ І ПОБУДОВА ГРАФІКІВ

Мета роботи – створення формул і графіків в MathCad.

Пояснення до виконання лабораторної роботи:

1 Запустити програму MathCad .

2 Створити на робочому аркуші MathCad цикл з метою визначення точок для побудови графіка.

3 Записати формулу функції у(х), для якої буде побудовано графік.

26

4 Звернутися до панелі Graph, вибрати на ній відповідний графік 5 Відформатувати графік.

Таблиця 1.1 – Варіанти завдання до лабораторної роботи № 1

27

Продовження таблиці 1.1

28

Продовження таблиці 1.1

побудувати для неї графік.

1 Записати цикл з метою визначення точок для наступної побудови графіка, який запишеться таким чином:

х:=-3,-2.9,..3.

1.1Звернутися до панелі Арифметика (Arithmetic).

1.2Обрати знак побудови циклу ( .. ) на панелі інструментів Матриця і ввести початкове значення аргументу x, крок його зміни (він дорівнює для всіх варіантів 0,1) та кінцеве значення аргументу.

2 Обчислити в циклі функцію y(x):= x (x-1).

3Вивести на екран значення функції y(x):= x (x-1) в точках х. Для чого представити запис у вигляді оператора y(x)=

4Побудувати графік функції y(x):= x (x-1).

4.1Звернутися на панелі інструментів Graph (График) до меню X-Y Plot (декартові координати).

4.2В області побудови графіка, що з’явиться, вказати наступні параметри: незалежну змінну х знизу графіка, зліва вказати функцію y(x). Натиснути клавішу F9. Графік буде побудовано.

5 Відформатувати графік. Для цього двічі натиснути на графік або звернутися в головному меню до команди меню Format/ Graph/ X-Y Plot. В діалоговому вікні Formatting Currently Selected X-Y Plot(Форматування графіка

вдекартових координатах) (рис.19 ) зробити наступні дії.

5.1Використати вкладку діалогового вікна X-Y Axes (рис. 19,а) і виконати відмітки Grid Line для осей Х і У (X-Axes і Y-Axes ), на графіку з’явиться сітка. Кількість ліній сітки для осей Х і У визначаться у вікні Number

of Grids. При цьому не повинне бути відмічене вікно Auto Grid.

Підписи під кожним значенням для сітки з’являються, якщо стоїть відмітка перед опцією Numbered. Якщо відмічено вікно Auto Scale, то програма MathCad автоматично створює шкалу подання сітки на графіку.

Можна нанести логарифмічну сітку на графік, якщо відмітити Log Scale. Використання Axes Style – Boxed, Crossed, None дозволяє зробити рамку навколо графіка, провести хрестоподібну лінію всередині його або не мати рамки, Equal Scales дає можливість зробити рівними лінії, які присутні на

графіку.

5.2.Дослідити характеристику кожної кривої на графіку за допомогою вкладки діалогового вікна (рис. 19, б) Traces. Використовуючи колонку Legend

29

Label (Підпис) задати ім’я графіка. Засіб представлення окремих точок графіка виконується за допомогою колонки Symbol (Маркер). Неперервна лінія на графіку буде зображена, якщо в колонці Line обрати значення solid.

Колір для подання ліній на графіку обирається за допомогою колонки Color. В колонці Туре (Тип лінії) вказати, що необхідно відмітити окремі точки на графіку (points), а не повести неперервну лінію.

Товщину лінії можна обрати, використовуючи колонки Weight. Якщо встановити прапорець Hide Arguments (Закрити параметри), то відображення назв осей на графіку не відбудеться. У разі відсутності прапорця Hide Legend

режимі відображення підпису прапорцем Show Title.

Рисунок 19 – Діалогове вікно задання засобів відображення графіків

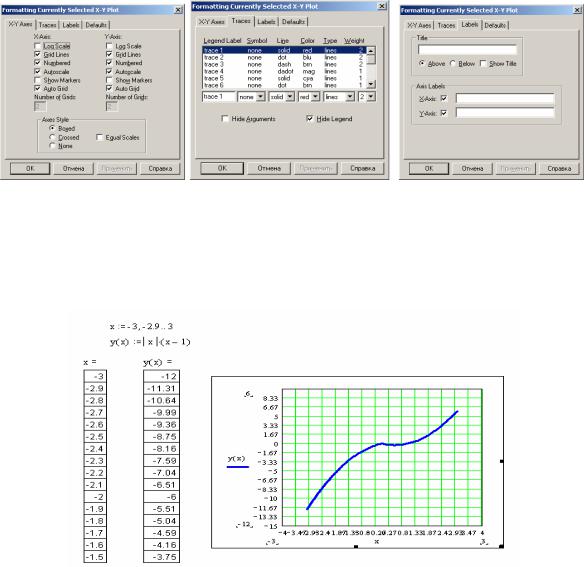
Остаточний результат обчислення значень функції і її графік матимуть наступний вигляд (рис. 20):

Рисунок 20 – Результат табулювання та графік функції

30