Посібник_MathCad_Лабор

;

.

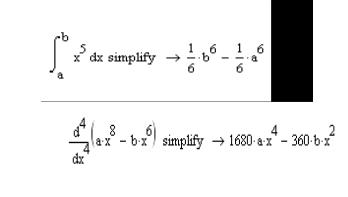
Контрольні питання

1 Як знайти у символьному вигляді визначені і невизначені інтеграли?

2 Чи можна застосовувати символьні операції до інтегралів по області, до тривимірних інтегралів, до контурних інтегралі?

3 Чи можна знайти в символьному вигляді похідні високих порядків?

Лабораторна робота №9

ОБЧИСЛЕННЯ ПОХІДНИХ У ЗАДАЧАХ ГЕОМЕТРІЇ І ЧАСТКОВИХ ПОХІДНИХ

Мета роботи – обчислення похідних в задачах геометрії і знаходження часткових похідних високих порядків в програмі MathCad .

Пояснення до виконання лабораторної роботи:

1 Скласти рівняння дотичної і нормалі до лінії, яка задана рівнянням y(x)=f(x) в точці М(x0,y0).

1.1Задати значення х0 і у0 в точці М.

1.2Записати рівняння лінії у(х).

обчислень і панель символів. Присвоїти значення похідної функції

61

2 Виконати символьне і чисельне обчислення часткових похідних вищого порядку від функції трьох змінних:

2.1Записати функцію, від якої будуть обчислюватися похідні другого

порядку.

2.2Звернутися до панелі обчислень і обрати оператор диференціювання.

2.3У відповідні місця заповнення оператора записати функцію, змінну для диференціювання і порядок диференціювання.

2.4 Натиснути правою кнопкою миші на знак оператора диференціювання і в контекстному меню обрати View Derivative As (Показати похідну як), встановити прапорець Partial Derivative (Часткова похідна).

62

Продовження таблиці 9.1

рівнянням y(x)=х4 -3х3+4х2-5х+1 в точці М(0,1).

1.1Задати значення х0 і у0 в точці М: х0:=0, у0:=1.

1.2Записати рівняння лінії у(х):= х4 -3х3+4х2-5х+1.

63

обчислень і панель символів. Присвоїти значення похідної функції уу(х): = dxd y(x) .

1.4 Записати рівняння дотичної у вигляді

tang (x) := yy(x0) (x − x0) + y0 ;

tang (x) → −5 x + 1.

1.5 Аналогічно записати рівняння нормалі

1.6Побудувати графіки дотичної і нормалі.

1.7Відформатувати графіки.

x0:=0, y0:=1,

y(x) := x4 −3 x3 +4 x2 −5 x +1, dxd y(x) →4 x3 −9 x2 +8 x −5,

64

2.2 У відповідні місця заповнення оператора записати функцію, змінну для диференціювання і порядок диференціювання.

2.3 Натиснути правою клавішею миші на знак оператора диференціювання і в контекстному меню обрати View Derivative As (Показати похідну як), установити прапорець Partial Derivative (Часткова похідна) (рис.32):

2.4Відмітити оператор диференціювання і звернутися до панелі Символіка/Обчислити/В символах.

2.5Задати числові значення для змінних, від яких обчислюється похідна х:=1, y:=1, z:=1.

2.6Обчислити числові значення похідних.

f (x, y, z):=x2ex + z − y z,

∂z2

px2:=2 exp(x) +4 x exp(x) +x2 exp(x), x := 1, y := 1, z := 1,

px2 = 19.028, py2 = 0,

pz2 = 0.

Рисунок 32 – Діалогове вікно Показати похідну

Контрольні питання

1 Як знайти дотичну до будь-якої кривої в MathCad? 2 Як знайти нормаль до будь-якої кривої в MathCad?

3 Як виконати символьні обчислення часткових похідних високого порядку?

4 Як виконати числові обчислення часткових похідних високого порядку?

65

Лабораторна робота №10

ОБЧИСЛЕННЯ ІНТЕГРАЛІВ В ЗАДАЧАХ ГЕОМЕТРІЇ І МЕХАНІКИ

Мета роботи – обчислення інтегралів в задачах геометрії і механіки в програмі MathCad .

Пояснення до виконання лабораторної роботи:

1 Обчислити площину плоскої фігури, обмеженої заданими лініями:

1.1Записати рівняння кривих, які обмежують площу плоскої фігури.

1.2Знайти точки їх перетину, для використання у двократному інтегруванні.

1.3Звернутися на панелі Символи до функції simplify.

1.4Увести оператор інтегрування. У відповідних містах записати ім’я першої змінної і границі інтегрування.

1.5На місці введення функції під інтегралом ввести ще один оператор інтегрування, границі інтегрування і підінтегральну функцію

S = ∫∫dxdy .

D

2 Обчислити координати центру тяжіння пластини:

2.1Записати рівняння кривих які описують область D пластини.

2.2Знайти точки їх перетину, для використання їх у двократному інтегруванні.

2.3Знайти площу S однорідної пластинки через подвійний інтеграл.

2.3.1Звернутися на панелі Символи до функції simplify.

2.3.2Увести оператор інтегрування. У відповідних містах заповнити ім’я першої змінної і границі інтегрування.

2.3.3На місці введення функції під інтегралом увести ще один оператор інтегрування, границі інтегрування і підінтегральну функцію

S =∫∫dxdy..

D

2.4 Знайти аналогічно статичні моменти Mx i My пластини відносно осей Ох і Оу як подвійні інтеграли

2.5 Визначити координати центру тяжіння як відношення підінтегральної функції, яка визначає статичні моменти пластини відносно осей Ох і Оу

66

Таблиця 10.1 – Варіанти завдання до лабораторної роботи №10

67

Продовження таблиці 10.1

x+y=6:

1.1 Знайти координати точок перетину заданих ліній, для чого необхідно розв’язати систему рівнянь (однією з вбудованих функцій MathCad, графічно

або розв’язавши систему рівнянь).

x=4y-y2, x+y=6.

Урезультаті будуть одержані точки перетину А(4;2) і В(3;3).

1.2Записати формулу для обчислення площі через кратний інтеграл і використати на панелі Символи функцію simplify

.

Приклад 2 Обчислити координати центру тяжіння пластини, яка обмежена кривими y2=4x+4 i y2=-2x+4:

Площа

Статичні моменти відносно осей Ох і Оу

68

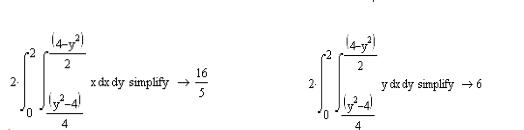
Координати центру тяжіння

Контрольні питання

1 Які геометричні характеристики можна обчислити з використанням інтегралів?

2 Як обчислити центр тяжіння через інтеграли?

Лабораторна робота №11

РОЗВ’ЯЗОК ЗВИЧАЙНИХ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ В MATHCAD

Мета роботи – з використанням вбудованих функцій і блочної структури знайти розв’язок звичайних диференційних рівнянь.

Пояснення до виконання лабораторної роботи:

1 Знайти розв’язок звичайного диференціального рівняння y/=f(x,y) з використанням «блоку розв’язань».

1.1Увести ключове слово given (дано), з якого починається блок розв’язань.

1.2Записати рівняння, використовуючи знак логічної рівності між правої

ілівою частинами рівняння з панелі управління Evaluation (Вирази).

1.3Задати початкові значення змінній, яка присутня в рівнянні.

1.4Увести ключове слово Odesolve, яким закінчується блок розв’язань, тобто присвоїти функції, відносно якої розв’язується рівняння, значення Odesolve з параметрами інтервалу інтегрування.

1.5Визначити значення знайденої функції в точках інтервалу, для чого створити відповідний цикл.

1.6Побудувати і відформатувати графік знайденої функції в точках

інтервалу.

69

2 Знайти розв’язок звичайного диференціального рівняння з використанням вбудованої функції rkfixed:

2.1Задати початкові значення змінній, яка присутня в рівнянні.

2.2Записати рівняння, використовуючи знак логічної рівності між правою і лівою частинами рівняння із панелі управління Evaluation (Вирази).

2.3Задати кількість кроків інтегрування рівняння на інтервалі.

2.4Присвоїти функції, відносно якої розв’язується рівняння, значення rkfixed з параметрами: функція, інтервал інтегрування, кількість кроків на інтервалі інтегрування, оператор диференційного рівняння.

2.5Визначити значення знайденої функції в точках інтервалу, для чого створити відповідний цикл.

2.6Побудувати і відформатувати графік знайденої функції в точках

інтервалу.

Таблиця 11.1 – Варіанти завдання до лабораторної роботи №11

70