
- •Министерство образования Республики Беларусь
- •Содержание
- •З а д а н и е 1. Численное решение алгебраических уравнений
- •Краткие теоретические сведения
- •1. Метод простой итерации
- •В данном алгоритме число проделанных итераций подсчитывает параметр к, а правая часть выражения 1..4 обозначено как «fi». Точность решения – eps. Число итераций лучше ограничить.
- •2. Метод Ньютона
- •3. Метод секущих
- •4. Метод Вегстейна
- •5. Метод деления отрезка пополам
- •Варианты заданий
- •Контрольные вопросы
- •Задание 2. Аппроксимация функций
- •Краткие теоретические сведения
- •Интерполяционный многочлен Лагранжа
- •Тогда после нескольких преобразований получим:
- •Варианты заданий
- •Контрольные вопросы
- •Задание 3. Алгоритмы численного интегрирования
- •Краткие теоретические сведения
- •1. Формула прямоугольников.
- •2. Формула трапеций.
- •3. Формула Симпсона или формула парабол.
- •Контрольные вопросы
- •Задание 4. Деревья, «полиз», Хеширование
- •1. Деревья (нелинейные структуры данных)
- •2. Построение обратной польской записи
- •3. Понятие хеширования
- •Хеширование таким образом – это способ, который подразумевает использование значения ключа для определения его позиции в специальной таблице..
- •Схемы хеширования
- •2. “Польская запись”
- •Задания по вариантам
- •3. Задача хеширования
- •Учебно-методические материалы по дисциплине Основная литература
- •Дополнительная литература
- •Перечень методических материалов
Тогда после нескольких преобразований получим:
интерполяционный многочлен Ньютона-Грегори:
![]() .
.
Пример:
Пусть
требуется найти интерполяционный
многочлен для функции
![]() ,
имеющей в узлах
,
имеющей в узлах![]() ,
,![]() ,
,![]() ,
,![]()
значения
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Шаг h=1,m=4.
Вычислим конечные разности:
-
xi
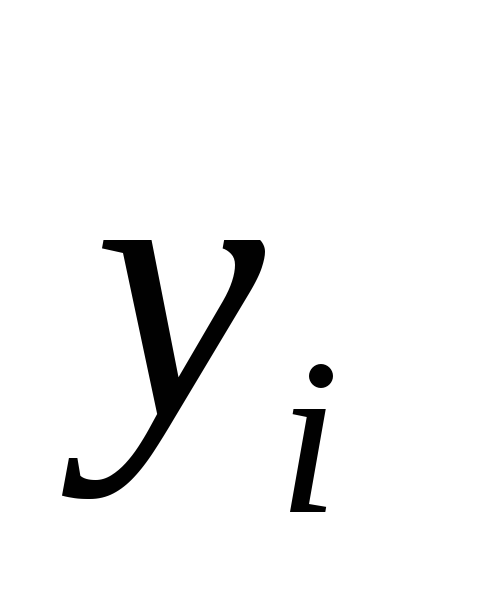
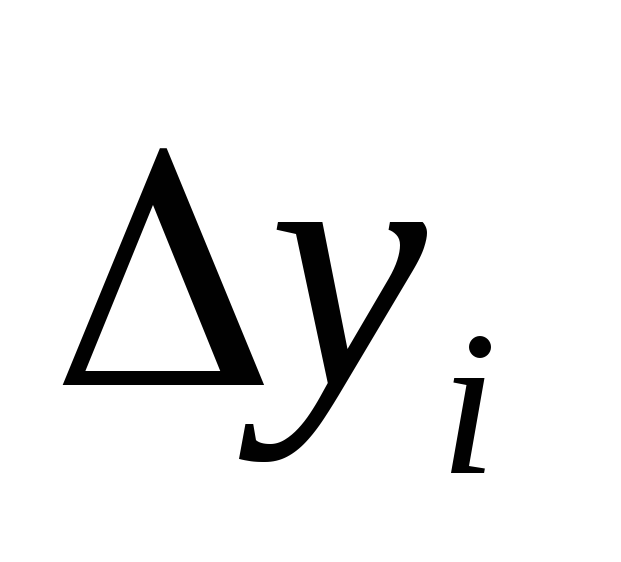
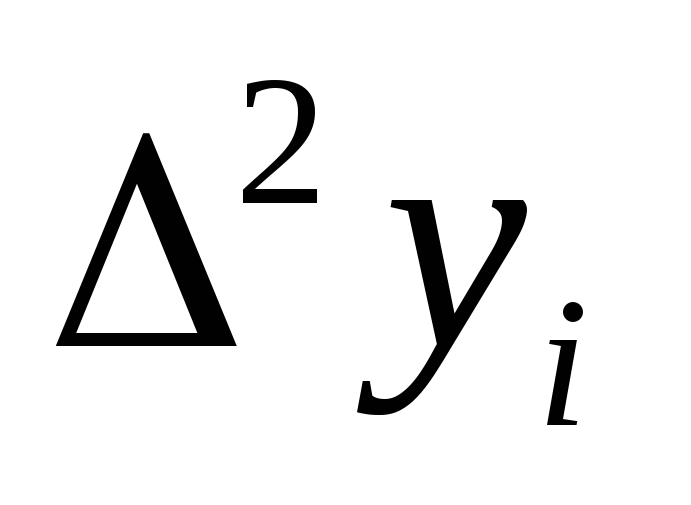
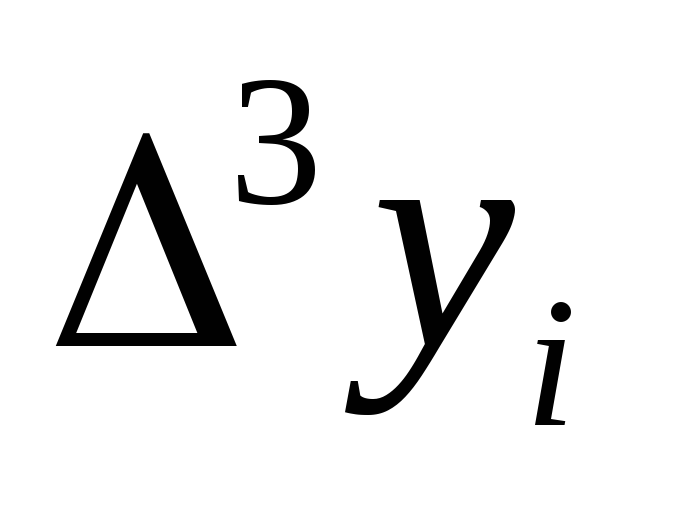
0
1
2
3
5
3
2
4
-2
-1
2
1
3
2
N3(x)=5+-2/(1!*1)(x-0)+1/(2!*12)(x-0)(x-1)+2/(3!*13)(x-0)(x-1)(x-2)
Аналитический вид полинома Ньютона-Грегори третьего порядка:
![]()
Варианты заданий
Во всех вариантах требуется аппроксимировать заданную исходную функцию f(x) многочленом Лагранжа на интервале [a, b], m - количество точек (узлов), в которых задана функция. Т.е. таблица исходной функции yi=f(xi) вычисляется в точках
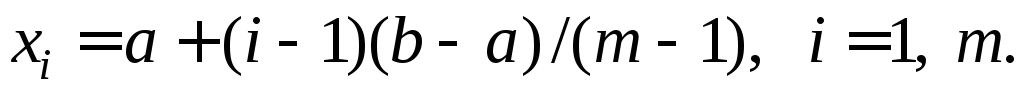
Используя полученную таблицу
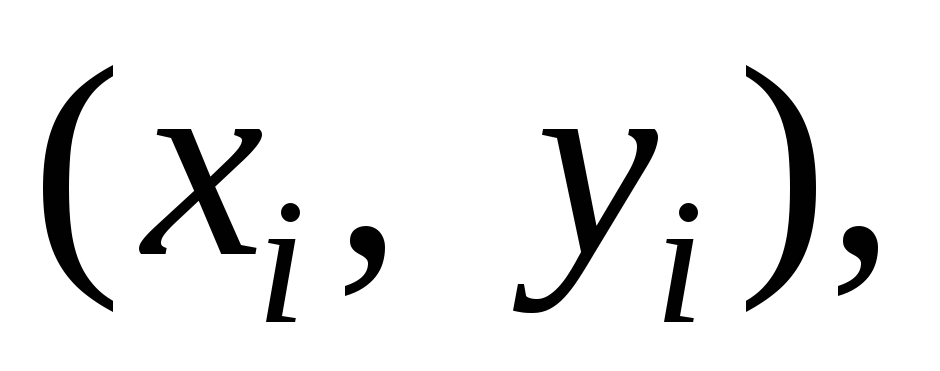 требуется вычислить значения функций
требуется вычислить значения функций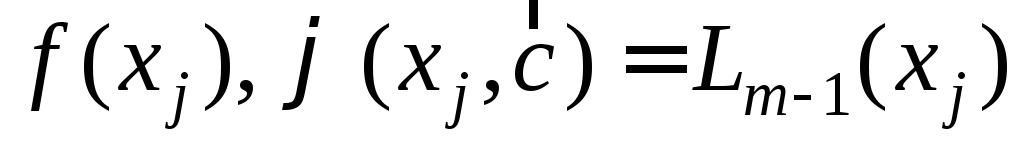 и погрешность
и погрешность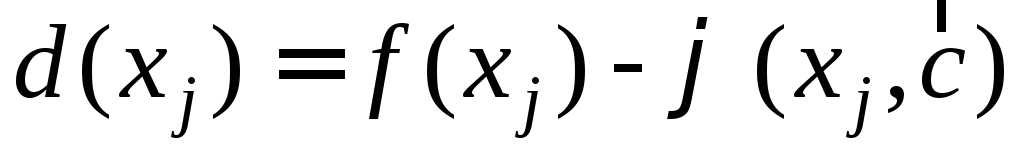 в точках
в точках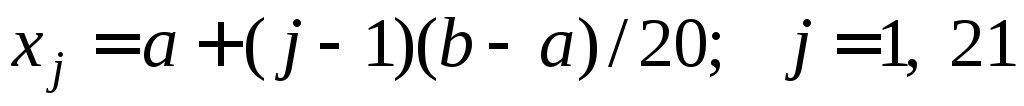
(в узловых точках d(xj=xi )=0)
Таблица 2.1
|
N |
Функция f(x) |
а |
В |
m |
|
1 |
|
-2 |
3 |
4 |
|
2 |
|
0 |
3 |
5 |
|
3 |
|
1 |
8 |
5 |
|
4 |
|
4 |
7 |
4 |
|
5 |
|
5 |
8 |
4 |
|
6 |
|
3 |
6 |
4 |
|
7 |
|
1 |
4 |
5 |
|
8 |
|
0 |
4 |
5 |
|
9 |
|
-8 |
2 |
5 |
|
10 |
|
-2 |
5 |
5 |
|
11 |
|
-5 |
3 |
5 |
|
12 |
|
-1 |
4 |
5 |
|
13 |
|
1 |
7 |
4 |
|
14 |
|
-3 |
5 |
4 |
|
15 |
|
-4 |
2 |
4 |
2. Для всех вариантов проведите линейную интерполяцию между двумя соседними узлами для десяти дополнительных промежуточных точек.
3.
Используя исходную таблицу yi=f(xi)
i=1,m,
получите аналитический вид полинома
Ньютона-Грегори Nm-1(x).
Требуется вычислить значения функций
![]() и погрешность
и погрешность![]() в точках
в точках![]()
Можно только теоретически !!!
4. Постройте графики и проанализируйте качество полученной аппроксимации.
Контрольные вопросы
1. Как ставится задача линейной аппроксимации функций?
2. Что такое интерполяция, ее геометрическая интерпретация?
3. Напишите интерполяционный многочлен Ньютона 2-го порядка.
4. Напишите интерполяционный многочлен Лагранжа 2-го порядка.
5. Как получить формулу линейной интерполяции?
Задание 3. Алгоритмы численного интегрирования
Цель работы: изучить приемы составления алгоритмов и написания программ для вычисления определенных интегралов. Научиться вычислять определенные интегралы с заданной точностью.
Краткие теоретические сведения
Задача численного вычисления определенного интеграла заключается в определении суммы ряда значений подинтегральной функции по определенным алгоритмам.
Постановка
задачи: Найти определенный интеграл![]() ,
гдеf(x)– некоторая заданная на отрезке [a,b]
непрерывная функция.
,
гдеf(x)– некоторая заданная на отрезке [a,b]
непрерывная функция.
Для
простоты разобьем промежуток интегрирования
точками, равноудаленными с шагом h
друг от друга:
![]() и заменим искомый интеграл на сумму
интегралов на полученных элементарных
участках:
и заменим искомый интеграл на сумму
интегралов на полученных элементарных
участках:
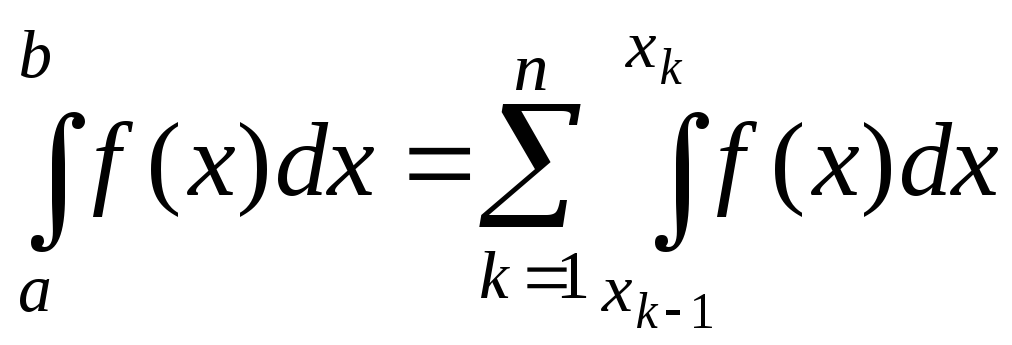 . (3.1)
. (3.1)
Заменяя подинтегральную функцию линейными полиномами получаем следующие квадратурные формулы.
1. Формула прямоугольников.
Аппроксимируем
площадь под графиком функции f(x)
суммой прямоугольников с основанием h
и высотой f(),
где
![]() .
.
1.a формула левых прямоугольников
![]() (3.2)
(3.2)
где:
![]() ,
,![]()
1.б формула правых прямоугольников
![]() (3.3)
(3.3)
где:.![]() ,
,![]()
1.в формула средних прямоугольников
![]() =Σcp,
где:
=Σcp,
где:
![]() . (3.4)
. (3.4)
т.е. здесь берем
средние точки элементарных участков:
![]() ,
,
Оценка
погрешности методов левых и правых
прямоугольников:
![]() ,
где
,
где![]() (3.5)
(3.5)
средних прямоугольников:
![]() ,
где
,
где![]() (3.6)
(3.6)
