Контрольные вопросы
1. Как решается задача нахождения корней уравнения?
2. В чем суть метода простой итерации и условие его сходимости?
3. Дайте геометрическую интерпретацию метода Ньютона.
4. В чем отличие метода Вегстейна от метода секущих?
5. Дайте геометрическую интерпретацию метода секущих (хорд).
Задание 2. Аппроксимация функций
Цель работы: изучить правила составления программ на языке Си, реализующих основные алгоритмы аппроксимации .функций. Освоить методику построения и использования алгебраических интерполяционных многочленов Лагранжа и Ньютона
Краткие теоретические сведения
Нахождение функции y=(x), близкой (т.е. аппроксимирующей) к некоторой исходной функции y=f(x)является одной из основных задач теории аппроксимации функций.
Интерполяция
является одним из способов аппроксимации
функций. Суть ее состоит в следующем. В
области значений x,
представляющей некоторый интервал [a,
b], где функции
f и
должны быть
близки, выбирают упорядоченную систему
точек (узлов).
(обозначим
их как вектор
),
число которых равно количеству искомых
параметров
.
Далее, параметры вектора
подбирают такими, чтобы функция
совпадала сf(x)
в этих узлах,
(2.1)
Наиболее
простой, хорошо изученной и нашедшей
широкое применение в настоящее время,
является линейная
аппроксимация,
при которой выбирают функцию
,
линейно зависящую от параметров
.
Для большинства практически важных приложений при интерполяции наиболее удобны обычные алгебраические многочлены, ибо они легко обрабатываются на ЭВМ.
Из математического анализа известно, что в силу теоремы Вейерштрасса, любую функцию можно с какой угодно точностью приблизить многочленом.
Пусть f(x) – функция, непрерывная на отрезке [a,b].
Выберем на этом отрезке узлы интерполяции:
.
Предположим, что в узлах интерполяции значения функции известны:
. (2.2)
Ставится задача: найти алгебраический многочлен Pn-1(x) такой, что
.
(2.3)
Интерполяционным многочленом называют алгебраический многочлен степени n-1, совпадающий с аппроксимируемой функцией в выбранных n точках.
Общий вид алгебраического многочлена
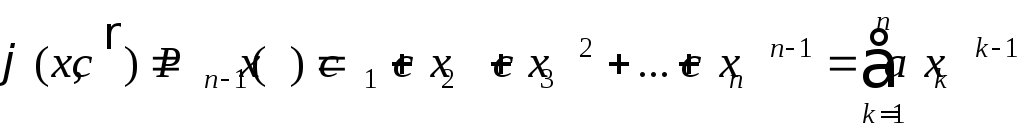(2.4)
Можно показать, что задача интерполяции посредством алгебраических многочленов имеет решение, причем единственное,
Оценка погрешности интерполяции:
,
где
. (2.5)
Интерполяционный многочлен Лагранжа
Многочлен
Лагранжа имеет вид:
где
(2.6.)
Очевидно, что
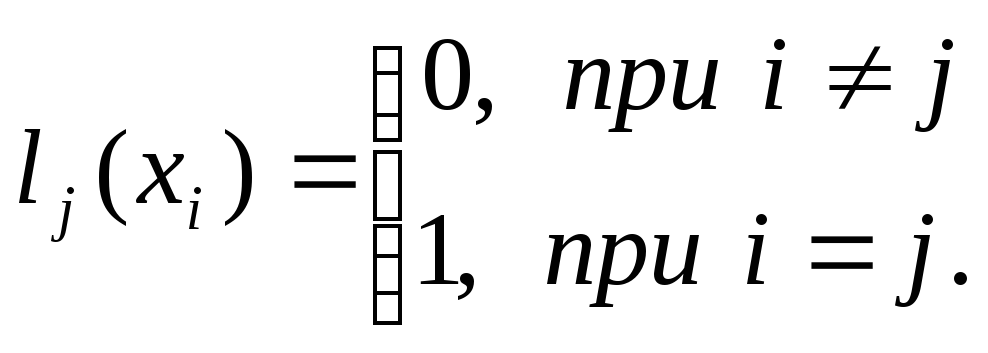а
,(2.7)
Линейная интерполяция
В общем случае для приближенного вычисления значения функции f в точке xТ находят в таблице ближайший к этой точке i-узел из общей таблицы, строят интерполяционный линейный многочлен вида:
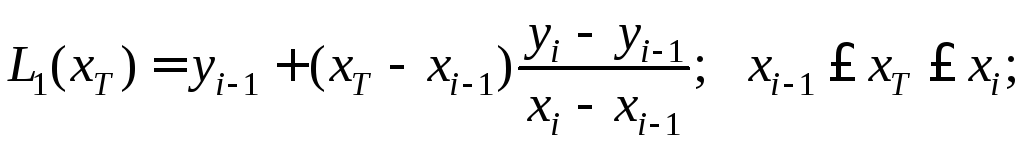(2.8)
и
за значение f(x)
принимают
(линейная
интерполяция)
Можно
показать, что погрешность линейной
интерполяции оценивается как:
где h – расстояние между соседними точками.
Интерполяционный многочлен Ньютона
Пусть
− набор узлов интерполирования,
− значения функции
в узлах.
Величину
называют конечной разностью первого
порядка вк-ом узле.
Аналогично определяются конечные разности высших порядков.
.
Разделенной разностью первого порядка называется выражение
,
.
Разделенной разностью второго порядка называется выражение
и т. д.
Используя представление функции f(x) в текущей точкеxчерез разделенные разности можно показать, что
. (2.9)
Очевидно, при
т. е.
− интерполяционный многочлен. Его
называют интерполяционным многочленом
Ньютона.
Рассмотрим случай равноотстоящих узлов, т. е. xi-xi-1=h