4. Метод Вегстейна

Этот метод является модификацией предыдущего метода секущих. В нем предлагается при расчете приближенного значения производной по разностной формуле использовать вместо точки в (1.7) точку, полученную на предыдущей итерации (рис. 1.5). Расчетная формула метода Вегстейна:

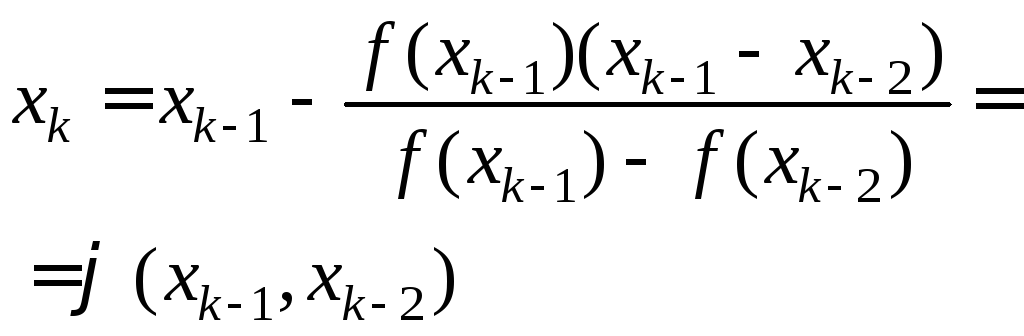
. (1.8)

Метод является двухшаговым (m=2), и для начала вычислений требуется задать 2 начальных приближения . Лучше всего. Метод Вегстейна сходится медленнее метода секущих, однако, требует в 2 раза меньшего числа вычисленийf(x) и за счет этого оказывается более эффективным.

Схема алгоритма представлена на рис. 1.6.

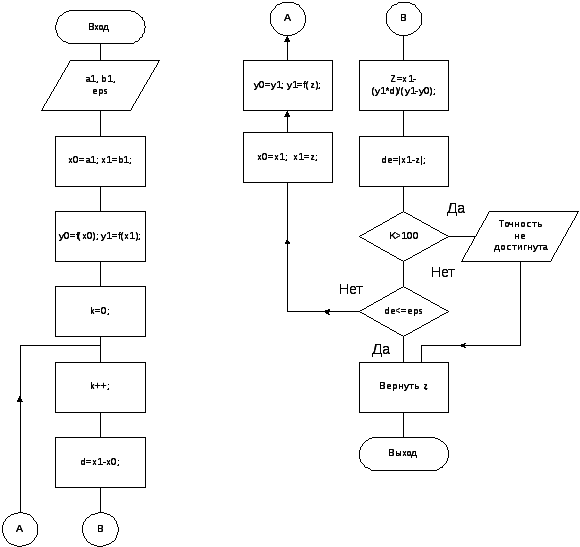
Рис. 1.6

В данной схеме границы интервала с корнем обозначены как [a1, b1]. Число допустимых итераций - 100

5. Метод деления отрезка пополам

Все вышеописанные методы могут работать, если функция f(x) является непрерывной и дифференцируемой вблизи искомого корня. В противном случае они не гарантируют получение решения.

Для разрывных функций, а также. если не требуется быстрая сходимость, для нахождения простого корня на интервале (, ) применяют надежный метод деления отрезка пополам. Его алгоритм основан на построении рекуррентной последовательности по следующему закону: в качестве начального приближения выбираются границы интервала, на котором точно имеется один простой корень далее находится его серединаочередная точкаx₃ выбирается как середина того из смежных с x₂ интервалов или, на котором находится корень. В результате получается следующий алгоритм метода деления отрезка пополам:

1. Вычисляем .

2. Вычисляем .

3. Если тогда

иначе .

4. Если тогда повторять с п.2.

5. Вычисляем

6. Конец.

За одно вычисление функции погрешность уменьшается вдвое, то есть скорость сходимости невелика, однако метод устойчив к ошибкам округления и всегда сходится.

Варианты заданий

1. По схеме, приведенной на рис.1.7 создать и отладить программу отделения всех корней функции f(x) на указанном интервале [a, b], в соответствии с полученным вариантом из табл. 1.1.

2. Далее создать программу уточнения корня указанным итерационным методом. Метод нахождения корня оформить в виде отдельной функции.

Выбрать точность =10^-3, =10^-4, =10^-5. Функция должна проверить правильность определения корня (f(x^*) приблизительно равна нулю).

3. Решить уравнение для выбранного интервала методом деления отрезка пополам

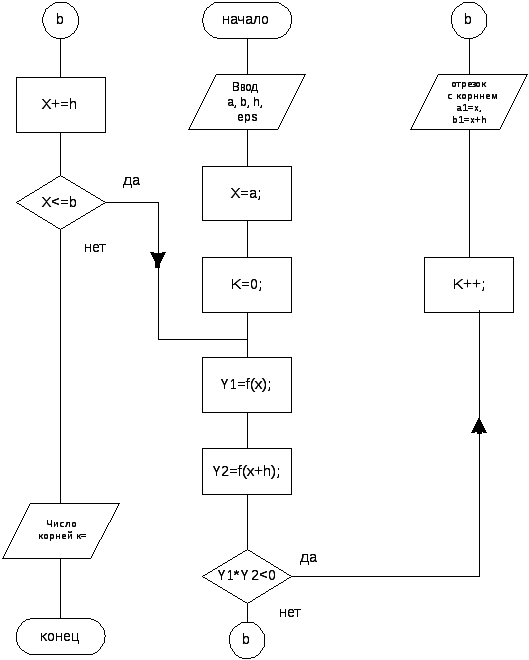
Рис.1.7

Таблица 1.1

N	f(x)	Интервал		методы
		А	B
1		-2	2	Метод простой итерации
2		-1	3	Метод секущих
3		1	8	Метод простой итерации
4		4	7	Метод простой итерации
5		4	8	Метод секущих
6		2	6	Метод простой итерации
7		3	9	Метод секущих
8		-4	0	Метод секущих
9		-12	5	Метод Ньютона
10		-2	5	Метод Ньютона
11		-6	2	Метод Ньютона
12		-4	2	Метод Ньютона
13		-7	3	Метод секущих
14		-4	3	Метод простой итерации
15		-4	4	Метод секущих

Примечание.

В табл. 1.1. все функции на указанном интервале имеют три корня.