
- •Змістовий модуль 1
- •Не 1.1. Структура системного програмного забезпечення Структура спз.
- •Місце ос в спз.
- •Поняття операційного середовища.
- •Операційні системи.
- •Системи керування файлами.
- •Інтерфейсні оболонки для взаємодії користувача з ос і програмні середовища.
- •Системи програмування.
- •Утиліти.
- •Основні функції ос.
- •Не 1.1. Базові поняття сучасних операційних систем Базові поняття операційної системи Linux. Файли, каталоги, робота з файлами. Права доступу до файлів і каталогів.Інструментарій.
- •Програми-фільтри. (немає) Командний інтерпретатор.
- •Змістовий модуль 2
- •Не 2.1. Загальна схема роботи компіляторів Визначення транслятора, компілятора, інтерпретатора.
- •Компілятор.
- •Різниця між інтерпретаторами і трансляторами.
- •Етапи трансляції.
- •Поняття проходу. Багатопрохідні і однопрохідні компілятори.
- •Не 2.2. Таблиці ідентифікаторів. Призначення та особливості побудови таблиць ідентифікаторів.
- •Найпростіші методики побудови таблиць ідентифікаторів.
- •Побудова таблиць ідентифікаторів методом бінарного дерева.
- •Не 2.3 Хеш-функції та хеш–адресація. Принципи роботи хеш-функцій.
- •Побудова таблиць ідентифікаторів на основі хеш-функцій.
- •Побудова таблиць ідентифікаторів методом ланцюжка.
- •Комбіновані способи побудови таблиць ідентифікаторів.
- •Змістовий модуль 3. Не 3.1.Кінцеві автомати. Визначення.
- •Детерміновані і недетерміновані кінцеві автомати.
- •Модель ка.
- •Розпізнавачі і перетворювачі. Визначення. Загальні поняття.
- •Класифікація розпізнавачів.
- •Не 3.2.Формальні мови та граматики. Способи завдання мов.
- •Операції над ланцюжками символів.(немає) Поняття мови.
- •Визначення формальної мови.
- •Визначення грамматики.
- •Класифікація граматик.
- •Способи задання схем грамтик Символічна, форма Наура-Бекуса, ітераційна форма й синтаксичні діаграми.
- •Чотири типи граматик по Хомському.
- •Правила побудови граматики із ланцюжка символів. (немає)
- •Змістовий модуль 4.
- •Не 4.1 Лексичні аналізатори (сканери).
- •Принципи побудови сканерів.
- •Призначення лексичного аналізатору.
- •Принципи побудови лексичних аналізаторів.
- •Граф кінцевого детермінованого автомата, що розпізнає граматику цілих чисел мови Сі(Немає) не 4.2.Синтаксичний та семантичний аналіз. Синтаксично-керований переклад.
- •Основні принципи роботи синтаксичних аналізаторів.
- •Дерево розбору. Перетворення дерева розбору в дерево операцій.
- •Призначення семантичного аналізу.
- •Етапи семантичного аналізу.
- •Ідентифікація лексичних одиниць мов програмування.
- •Розподіл пам’яті.
- •Не 4.3. Способи внутрішнього представлення програм Зв'язані облікові структури, що представляють синтаксичні дерева.
- •Багатоадресний код з явно іменованим результатом (тетради).
- •Багатоадресний код з неявно іменованим результатом (тріади).
- •Обернений (постфиксна) польський запис операцій.
- •Алгоритм Дейкстри.
- •Асемблерний код або машинні команди.
- •Розбір арифметичного виразу. Алгоритм Рутисхаузера.
- •Не 4.4 Генерація коду. Методи генерації коду.
- •Загальні принципи генерації коду.
- •Синтаксично керований переклад.
- •Змістовий модуль 5
- •Не 5.1. Керування процесами та ресурсами. Поняття обчислювального процесу та ресурсу.
- •Класифікація ресурсів.
- •Загальна схема виділення ресурсу.
- •Однопрограмний і мультипрограмний режими.
- •Основні риси мультипрограмного режиму.
- •Обчислювальні процеси.
- •Діаграма станів процесу.
- •Реалізація поняття послідовного процессу в ос.
- •Процеси і треди. (немає) Блок керування процесом.
- •Процеси в ос unix.
- •Події (переривання) - рушійна сила, що змінює стан процесів.
- •Механізм обробки переривань.
- •Функції механізму переривань.
- •Групи переривань.
- •Розподіл переривань по рівнях пріоритету.
- •Дисципліни обслуговування переривань.
- •Обробка переривань за участю супервізорів ос.
- •Не 5.2. Планування процесів та диспетчеризація задач. Функції ос, пов’язані з керуванням задач.
- •Організація черг процесів та ресурсів.
- •Priority queuing - (pq)
- •Стратегії планування.
- •Якість диспетчеризації та гарантії обслуговування.(Немає)
- •Безпріоритетні до: лінійні та циклічні.
- •Пріоритетні до: до з фіксованим пріоритетом та до з абсолютним пріоритетом.
- •Адаптивні до. (Немає) Визначення середнього часу знаходження заявки в системі. (Немає) Недоліки до з фіксованим пріоритетом.
- •Динамічне планування (диспетчеризація). (Немає) Диспетчеризація задач з використанням динамічних пріоритетів. Переваги і недоліки.
- •Критерії ефективності обчислювального процесу. (Немає) Методи підвищення продуктивності системи для багатопроцесорних систем.
- •Механізм динамічних пріоритетів в ос unix.
- •Змістовий модуль 6
- •Не 6.4. Керування пам’яттю. Пам'ять і відображення, віртуальний адресний простір.
- •Простий безперервний розподіл і розподіл з перекриттям (оверлейні структури).
- •Розподіл статичними і динамічними розділами.
- •Розділи з фіксованими границями. Розділи з рухливими границями.
- •Виділення пам'яті під новий розділ: перша придатна ділянка; сама придатна ділянка; сама невідповідна ділянка.
- •Сегментна, сторінкова і сегментно-сторінкова організація пам'яті. Сегментний спосіб організації віртуальної пам'яті.
- •Дисципліни заміщення: fifo; lru (1еаst recently used,); lfu (1еаst frequently used); random.
- •Сторінковий спосіб організації віртуальної пам'яті.
- •Сегментно-сторінковий спосіб організації віртуальної пам'яті.
- •Змістовий модуль 7
- •Не 7.1. Ос однопроцесорних кс. Класифікація ос.
- •Режими організації обчислювального процесу. (Немає) Основні принципи побудови операційних систем.
- •Принцип модульності.
- •Принцип функціональної вибірковості.
- •Принцип генерування ос.
- •Принцип відкритої і нарощуваний ос.
- •Принцип мобільності.
- •Принцип забезпечення безпеки обчислень.
Побудова таблиць ідентифікаторів на основі хеш-функцій.
Дивись попереднє питання.
Побудова таблиць ідентифікаторів методом ланцюжка.
Неповне заповнення таблиць ідентифікаторів при застосування хеш-функції веде до неефективного використання обсягу пам’яті. Цього недоліку можна уникнути якщо доповнити таблиці ідентифікаторів деякою проміжною хеш-таблицею. В комірках хеш-таблиці може зберігатися або порожнє значення або значення вказівника на деяку область пам’яті з основної таблиці ідентифікаторів. Тоді хеш-функція обчислює адресу, у якій відбувається звертання спочатку до хеш-таблиці, а потім через неї до самої таблиці ідентифікаторів. Якщо відповідна комірка таблиці ідентифікаторів порожня, то комірка хеш-таблиці буде містити порожнє значення. Таблиця буде динамічною і її розмір росте в міру заповнення. Такий підхід дозволяє отримати 2 позитивних ідентифікаторів:
немає необхідності заповнити порожніми значеннями таблицю ідентифікаторів, це можна зробити тільки для хеш-таблиці
кожному ідентифікатору буде відповідати тільки одна комірка в таблиці, це дає можливість економити пам’ять.
На основі цієї схеми можна реалізувати ще один спосіб реалізувати таблиці ідентифікаторів методів ланцюжків. Для цього методу таблиці ідентифікаторів для кожного елемента додається ще одне поле, в якому може містити посилання на будь-який елемент таблиці.
Приклад:
Нехай в нас є ряд послідовних комірок n1,n2,n3,n4,n5 і необхідно розмістити такі ідентифікатори: A1,A2,A3,A4,A5
h(A1)=h(A2)=h(A5)=n1
h(A3)=n2
h(A4)=n4
заповнення хеш-таблиці і таблиць ідентифікаторів методом ланцюжків:
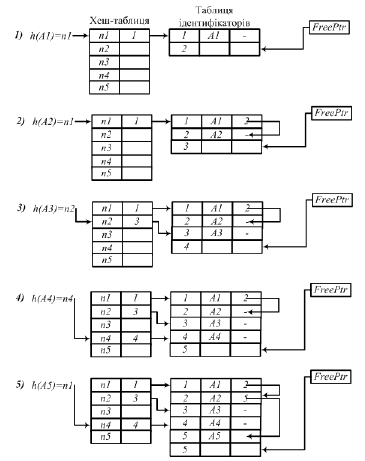
A1 – одне порівняння
A2 – два порівняння
A3 – одне порівняння
A4 – одне порівняння
A5 – три порівняння
Середній час розміщення і пошук в таблиць ідентифікаторів залежить тільки від числа колізій. Цей метод дозволяє більш ощадливо використовувати пам'ять, але вимагає організації роботи з динамічними даними.
Комбіновані способи побудови таблиць ідентифікаторів.
В комбінованих методах таблиці ідентифікаторів організовується спеціальне додаткове поле, через яке здійснюється пошук ідентифікаторів, для яких виникла колізія. При відсутності колізій поле посилань залишається порожнім.
Ефективність методу залежить від якості хеш-функції і від методу організації додаткових сховищ даних.
Змістовий модуль 3. Не 3.1.Кінцеві автомати. Визначення.
Кінцевий автомат (у сучасній англомовній літературі використовується також виразніше, на погляд автора, позначення, що не має хорошого російського еквіваленту, — state machineщо дослівно переводиться як машина достатків) є пристроєм, що має внутрішню пам'ять (змінні достатки), а також набір входів і виходів. Об'єм внутрішньої пам'яті в кінцевих автоматів, як випливає з назви, кінцевий. Автомати з необмеженим об'ємом внутрішньої пам'яті називаються безконечними автоматамине реалізовуються і використовуються лише в теоретичних Побудовах (Мінський 1971].
Проте деякі різновиди теоретично безконечних автоматів — наприклад, стекові — можуть бути реалізовані у формі автоматів з практично необмеженою пам'яттю — наприклад, досить глибоким стеком — і знаходять практичне вживання, наприклад при синтаксичному аналізі мов з вкладеними структурами [Кормен/лейзерсон/рівест 2000].
Робота автомата полягає в тому, що він аналізує достатки своїх входів, і, залежно від значень входів і свого внутрішнього достатку, змінює значення виходів і внутрішній достаток. Правила, в з ответствії з якими відбувається зміна, описуються таблицею або діаграмою переходів. Діаграма переходів є граф, вершини якого відповідають допустимим достаткам внутрішніх змінних автомата, а ребра — допустимим переходам між ними. Переходи між вершинами направлені: наявність переходу з А у В не означає, що існує перехід з У в А. Налічие переходу в обох напрямах символізується двома ребрами, що сполучають одну пару вершин. Такий граф називається орієнтованим [Кормен/лейзерсон/рівест 2000]. Таблиця переходів може розглядатися як матричне представлення діаграми переходів.
Блок-схеми (мал. 10.5) є звичайним способом візуалізація графів переходів і використовуються для опису алгоритмів з 60-х років. Будь-який алгоритм, що виконується на фон-неймановськом комп'ютері з кінцевим об'ємом пам'яті (а також будь-який фізично здійснимий алгоритм), може бути описаний як кінцевий автомат і змальований у вигляді блок-схеми.
В кінцевих автоматів з обмеженим числом допустимих значень входів, граф переходів завжди кінцевий, хоча і може містити цикли (замкнуті дороги) і контури (сукупності різних доріг, що приводять до однієї і тієї ж вершини). Зрозуміло, що для автомата з графом, що містить цикли, неможливо гарантувати фінітності — завершення роботи за кінцевий час. Як відомо, завдання доказу фінітності алгоритму, хоча і вирішена в багатьох окремих випадках, в спільному випадку алгоритмічно нерозв'язна .
