2.4. Екситон – фононна взаємодія

Як тільки ми вияснили природу електронного збудження, яке відповідає за утворення оптичного спектру кристалу в конкретній частотній області, появилась необхідність в детальному дослідженні механізмів диссипації енергії збудження та динамічних властивостей екситона. Справді, в ідеальних кристалах, у яких відсутні домішки, дефекти, дислокації, а молекули зафіксовані в рівноважних положеннях гратки кристалу, при поглинанні світла основним процесом є перетворення фотона в екситон і зворотній перехід екситона в фотон. В таких кристалах спектр поглинання являв би собою вузькі резонансні лінії з безкінечно малою напівшириною, яка, власне, й визначається оберненим часом життя збудження. Проте на експерименті спостерігаються досить широкі смуги поглинання, що природньо вимагає від нас поглибленого вивчення релаксаційних механізмів, які спричинюють помітне зменшення часу життя екситонного збудження. Характер цих механізмів може бути найрізноманітніший і залежить від типу кристалу та його структури.

І на першому місці тут стоїть необхідність враховувати в процесах розсіювання екситонів коливання атомів гратки кристалів – фононів. Цей аспект в теорії відгуку є надзвичайно важливим і виключити з розгляду фононну підсистему неможливо за жодних умов. Адже, навіть при температурі абсолютного нуля можливі процеси, що супроводжуються народженням коливного збудження кристалічної гратки.

В нашій роботі ми розглянемо взаємодію екситона Ваньє-Мотта з коливаннями атомів гратки кристалу. Річ в тім, що екситонне збудження неорганічних напівпровідників характеризується воднево-подібною серією m-енергетичних рівнів, які мають кінцеву ширину зони в області зміни значень квазіімпульсу екситона y – E_m(y) і кожен з яких по різному може бути зв’язаний з фононним спектром кристалу. Виявляється, наприклад, що функція екситон-фононного зв’язку зменшується зі збільшенням номера екситонної зони, а це означає, що відповідним чином повинен і змінюватись увесь оптичний спектр екситонного збудження напівпровідника. Це вимагає ознайомлення зі специфікою коливного спектру кристалу – наявністю акустичної та оптичної віток фононних збуджень в напівпровідниках. Особливу увагу було звернуто на взаємодію екситонів з оптичною віткою коливань атомів гратки, так як вона визначає найбільший вклад в екситонну смугу екситонного поглинання. В курсовій роботі проводиться дослідження оптичних екситонних спектрів шаруватих напівпровідників типу InSe, зроблено розрахунок спектрального розподілу функції форми екситонного поглинання, вивчена динаміки температурного генезису функції форми кривої екситонного поглинання.

2.5. Екситонний спектр в шаруватих кристалах

Побудовано теорії екситонних спектрів у іонних напівпровідниках, які досить детально і адекватно описують формування та генезис екситонних спектрів при їх взаємодії з фононами. У цих дослідженнях обмежувалися розглядом переважно основного екситонного стану, тоді як у області довгохвильового краю смуги фундаментального поглинання багатьох кристалів спостерігаються добре розділені спектральні лінії, походження яких приписується переходам у вищі екситонні стани.

Встановлення механізмів переходу у вищі екситонні стани та їх впливу на положення, ширину і форму смуг поглинання також важливе для адекватного трактування результатів експериментальних досліджень температурних змін екситонних спектрів. Енергії таких переходів зазвичай визначаються формулою

, (2.9)

де n – головне квантове число стану, E_g – ширина забороненої зони, – стала Рідберґа для екситона,– зведена маса електрона і дірки. Проте, експериментально встановлені положення екситонних піків часто виявляються зміщеними порівняно з визначеними за формулою (2.9), особливо у випадкуn = 1. Причини таких зміщень пов’язуються з анізотропією зонного спектра, впливом поверхонь, деформаціями, відхиленнями від тривимірної моделі екситона у сильноанізотропних і шаруватих кристалах та ін. Роль екситон-фононної взаємодії у цих процесах досі не досліджувалася, хоча відомо, що вона може спричиняти зміщення та розширення екситонних ліній.

Дослідження характеру температурних змін смуг екситонних переходів у nS-стани (n = 1, 2, 3) у напівпровідникових кристалах зі слабким електрон-фононним зв’язком можна використовувати модель екситон Ваньє-Мотта, утвореного внаслідок прямого фотопереходу електрона з валентної зони, коли .[11] Відомо, що частотна залежність коефіцієнта поглинання, обумовленого такими переходами, подається у вигляді функції

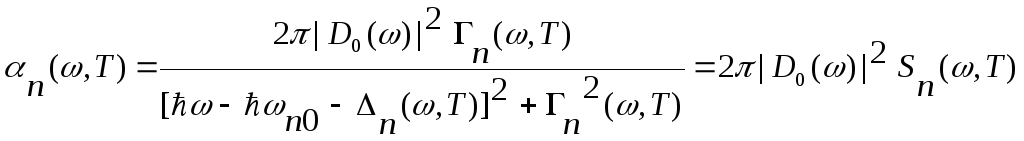, (2.10)

де

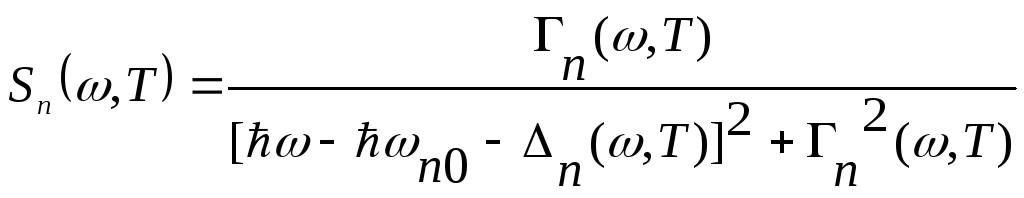(2.11)

функція форми екситонної смуги поглинання, пов’язаної з переходом у nS-стан; D₀ – дипольний електричний момент екситона; ħω – енергія збуджуючої хвилі; ħω_n0 – енергія екситона у стані nS; і– дійсна та уявна частини масового оператора

(2.12)

відповідної функції Ґріна

(2.13)