
- •Introduction
- •Experimental procedure
- •Magnetic properties of solid-state materials
- •Magnetic properties of layered oxides
- •α-NaFeO2
- •LiNiO2
- •LiNi1yCoyO2
- •Magnetic properties of spinels
- •LiMn2O4
- •LiMn2yCoyO4
- •Magnetic properties of Li-phosphates
- •Phospho-olivine LiFePO4
- •LiMPO4 olivine-related compounds
- •LixM2(PO4)x compounds
- •Conclusion
- •References

Ionics (2006) 12: 21–32
DOI 10.1007/s11581-006-0007-5
ORIGINAL PAPER
C. M. Julien . A. Ait-Salah . A. Mauger . F. Gendron
Magnetic properties of lithium intercalation compounds
Received: 13 December 2005 / Accepted: 25 January 2006 / Published online: 26 April 2006
# Springer-Verlag 2006
Abstract Magnetic experiments are powerful tools to study fundamental properties and to check the qualities of samples. Temperature, stress, and impurities of materials can all affect magnetic properties and play an important role in the utilization of these materials for engineering applications. The estimation and analysis of the spontaneous magnetization can reveal ferromagnetic particles as impurities in samples. The shape of the temperature dependence of magnetization is indicative of the origin of the magnetic properties. However, it is necessary to correlate the χm(T) curves and isothermal M(H) plots to achieve a complete analysis of the electronic properties of the materials. Highlights of magnetic properties of lithium intercalation compounds are briefly described. Intrinsic and extrinsic properties are considered as useful parameters to determine the purity of electrode materials for rechargeable Li-ion batteries.
Keywords Li-ion batteries . Intercalation compounds . Magnetic properties . Clustering
Introduction
Magnetism continues to be an important subject, both to provide insights into the understanding of condensed matter and cooperative phenomena and for the development of technologically important materials and devices. Materials may be classified into five categories by their
C. M. Julien (*) . A. Ait-Salah . F. Gendron Institut des Nano-Sciences de Paris (INSP), Université Pierre et Marie Curie, CNRS-UMR 7588,
Campus Boucicaut, 140 rue de Lourmel, 75015 Paris, France
e-mail: christian.julien@insp.jussieu.fr
A. Mauger
Department MIPPU, CNRS,
Campus Boucicaut, 140 rue de Lourmel, 75015 Paris, France
responses to externally applied magnetic fields, i.e., dia-, para-, ferro-, ferri-, and antiferromagnetic substances. The study of magnetic properties in the solid state implies an examination of the interaction between the electrons associated with the metal ions, which are substancespecific. Consequently, these magnetic properties differ greatly in strength. Diamagnetism is a property of all materials and opposes applied magnetic fields, but it is a very weak phenomenon. Paramagnetism, when present in semiconductors, can be stronger than diamagnetism and produces magnetization in the direction of the applied field, and proportional to the applied field. Ferromagnetic and ferrimagnetic effects are very large: They produce magnetizations sometimes orders of magnitude larger than the applied field and, as such, are much larger than either diamagnetic or paramagnetic effects.
Magnetic measurements can be extended to study magnetic structure and electronic properties of materials used in lithium power sources, i.e., the so-called lithium intercalation compounds (LiICs). Because Li ions are nonmagnetic (diamagnetic), they indirectly affect magnetic properties through influence on the cation valence of the 3d iron-transition element. Magnetic properties are determined by the structure of sublattice in the oxide framework, the nature of the metal ions, and the electronic states. In this context, magnetic properties are of particular interest because they are found to be a powerful tool to characterize materials, in particular, when impurities and nanoparticles cannot be detected by classical analysis, i.e., X-ray diffraction (XRD), Fourier transform infrared (FTIR) spectroscopy, etc. Magnetism is therefore indirectly important to the electrochemical properties of materials as well.
Magnetic measurements are also tools used to check the quality of samples. The estimation and analysis of the spontaneous magnetization can reveal the existence of ferromagnetic (ferrimagnetic) particles in samples. The shape of the temperature dependence of magnetization M (H) is indicative of the origin of the magnetic properties. However, it is necessary to correlate the magnetic susceptibility χm(T) curves and isothermal M(H) plots for a
22
complete analysis of the electronic properties of materials [1].
One goal of the work carried out in our laboratory is the understanding of the local structure in LiICs using resonance spectroscopy, i.e., Raman scattering, Fourier transform infrared, electron spin resonance, and magnetic measurements. This paper presents the magnetic properties of some LiICs to correlate the structural and electronic properties of oxides used as positive electrode materials in rechargeable lithium-ion batteries. Here, we consider typical materials such as compounds of the α-NaFeO2- type structure, i.e., LiNiO2 and LiFeO2; Li–Mn–O frameworks with the spinel structure, i.e., LiMn2O4 and LiCoMnO4; and the phospho-olivine lattices, i.e., LiFePO4, LiMnPO4, and LiNiPO4. The characterization of the magnetic nanoparticles incorporated in these frameworks is deduced from the magnetic susceptibility and magnetization measurements.
Experimental procedure
Nowadays, most of the magnetic properties are studied by various techniques such as neutron diffractometry, magnetometry, NMR, and electron spin resonance. The two resonance spectroscopies are also useful tools for characterizing the local structure in materials.
The microscopic magnetic structure of materials is most often studied by using neutron scattering techniques, and experiments are performed to measure the structure and excitation for all classes of magnetic materials. More recently, synchrotron sources have been used to study the magnetic scattering. The range of wavelength and energy possessed by thermal moderated neutrons allows us to study not only the nuclear long-range, static nature of solids, but also the dynamics (phonons). Similarly, the neutron’s magnetic moment (S=1/2) can be used as a probe to study the magnetism in solids, allowing unparalleled scrutiny of both the magnetic structures (shortand longrange) and the excitations (magnons) of magnetic materials. Neutron scattering techniques are presently considered as the most powerful probe of magnetic materials. When a material has ferromagnetic ordering, the magnetic lattice is
the same as the atom lattice, and no new “Bragg reflections” are created (the intensities of existing Bragg reflections change). For an antiferromagnetic state, however, the magnetic lattice is not the same as the atom lattice, and new, purely magnetic Bragg reflections occur. From the pattern of the magnetic Bragg reflections, the details of the antiferromagnetic ordering structure can be deduced, in the same way that crystal structures are solved from the pattern of the (nonmagnetic) Bragg peaks in XRD and (nuclear) neutron diffraction. Neutron diffraction patterns are currently analyzed using the Rietveld fitting procedure [2].
The use of superconducting quantum interference devices (SQUID) in ultrasensitive magnetic measurement systems may nowadays be considered as a standard technique, to the extent that several companies offer reliable and automated commercial SQUID magnetometers. The SQUID consists of two superconductors separated by thin insulating layers to form two parallel Josephson junctions. The device uses a liquid-helium- cooled amplifier to measure the magnetic moment in the range from 10−7 to 300 emu. The field range is from −5.5 to +5.5 T [3].
Data on the temperature dependence of susceptibility are currently recorded on heating the sample using two modes to determine the magnetic behavior: zero-field cooling (ZFC) and field-cooling (FC). The procedure is based on performing two consecutive magnetization measurements: In ZFC, the sample is first cooled down in the absence of a magnetic field and then measured in an applied magnetic field at increasing temperature, FC is performed in a similar magnetic field at decreasing temperature. The results obtained in this way can exhibit a strong dependence of magnetization. The temperature range in which a magnetic hysteresis appears and the temperature at which a magnetic ordering can be detected should be emphasized.
Magnetic properties of solid-state materials
This section summarizes the general trends of magnetic properties for solid-state materials. In electrical engineering, the magnetic susceptibility is the degree of magneti-
Fig. 1 Temperature dependence |
Paramagnetism |
Ferromagnetism |
Antiferromagnetism |
||||
of the magnetic susceptibility of |
|
|
|
|
exchange |
|
exchange |
paramagnetic, ferromagnetic, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
and antiferromagnetic solids |
|
|
|
|
integral >0 |
|
integral <0 |
|
|
|
|
|
|||
χ |
|
0 |
T |
χ m = C T
T
χ |
|
|
|
|
|
|
|
|
χ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Complex behavior |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 T |
|
T |
|
|
|
|
|
|
|
|
||||
θ |
0 T |
|
T |
|||||||||||
|
|
χ |
= |
C |
|
|
|
|
χ |
= |
C |
|||
|
|
T − T |
|
|
|
|
T + θ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
23
Table 1 Electron configurations and net spins for transition element cations and effective magneton numbers for iron group ions [5]
Ion |
Configuration |
Basic level |
Free cation |
|
Cubic field |
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
peff |
S |
peff |
|
Mn4+, Cr3+ |
3d3 |
4F3/2 |
3/2 |
3.87 |
3/2 |
3.87 |
|
Mn3+, Cr2+ |
3d4 |
5D0 |
2 |
4.90 |
1 |
2.83 |
|
Fe3+, Mn2+ |
3d5 |
6S5/2 |
5/2 |
5.92 |
1/2 |
1.73 |
|
Fe2+, Co3+ |
3d6 |
5D4 |
2 |
4.90 |
0 |
0 |
|
Co2+, Ni3+ |
3d7 |
4F9/2 |
3/2 |
3.87 |
1/2 |
1.73 |
|
Ni2+ |
3d8 |
3F4 |
1 |
2.83 |
1 |
2.83 |
|
Cu2+ |
3d9 |
2D5/2 |
1/2 |
1.73 |
1/2 |
1.73 |
|
The free ions and cations in strong cubic fields are considered
zation of a material, M is the magnetic dipole moment per unit volume in response to a magnetic field H, as
@M
χm ¼ @ : (1)
H
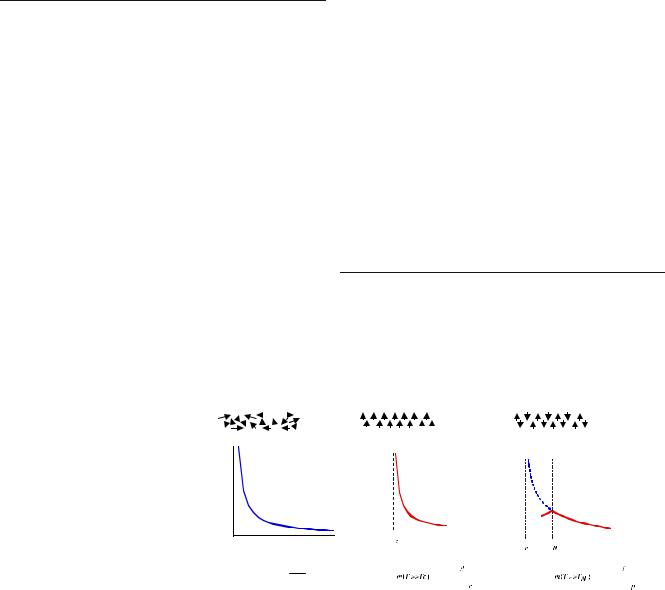
If χm is positive, the material is called paramagnetic and the magnetic field is strengthened by the presence of the material. If χm is negative, then the material is diamagnetic and the magnetic field is weakened in the presence of the material. Figure 1 displays the temperature dependence of the magnetic susceptibility of paramagnetic, ferromagnetic, and antiferromagnetic solids [4].
Paramagnetic materials attract and repel like normal magnets when subjected to a magnetic field. For thermal equilibrium, the magnetization of paramagnets is treated using the Brillouin formalism. Under relatively low magnetic field saturation when the majority of atomic dipoles are not aligned with the field, paramagnetic materials exhibit magnetization according to the wellknown Curie–Weiss law, which treats the interaction between spins and molecular field
where S refers to the electronic spin quantum number. Equation (4) is used in the case of the “quenching” of the orbital angular momentum (L=0 and J=S), which occurs frequently for transition-metal ions from the iron group. Table 1 shows the theoretical magneton numbers for iron group ions. Paramagnetic ions with electronic spin, S (e.g., S=3/2 for d3 ions Mn4+ and Cr4+), are associated with magnetic moments, μeff=−gμBS, that align in the presence of static magnetic field H0.
When the Curie constant is determined experimentally by fitting the linear χm−1(T) curve in the paramagnetic domain, one can estimate the experimental value for peff and then know the electronic configuration of the magnetic ion (in the quenched configuration) using the following equation:
exp |
|
3kBCp |
|
1=2 |
2:84 |
Cp: |
(5) |
|
peff |
¼ |
N |
μ2 |
¼ |
||||
|
|
A B |
|
|
p |
|
||
An important class of magnetic materials is that of ferromagnets: iron, nickel, cobalt, and manganese. A ferromagnetic substance possesses a spontaneous magnetic moment even in the absence of an applied magnetic field.
|
Cp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
χm ¼ T þ θp |
; |
|
|
|
|
|
(2) |
(emu/mol) |
0.06 |
T =11 K |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
where Cp is the Curie constant. The Weiss constant, θp, |
|
|
|
|
|
α-NaFeO2 |
|
||||||||||
typically accounts for magnetic ordering of the electronic |
|
|
|
|
|
|
|
|
|||||||||
moments |
below |
the |
Curie |
or |
Néel temperature |
for |
m |
0.04 |
|
|
|
H=0.5 Tesla |
|
||||
uncorrelated |
spins (in |
salts, |
for instance) θp=0 |
(see |
χ |
|
|
|
|
|
|
|
|||||
susceptibility |
|
|
|
|
|
|
|
||||||||||
Fig. 1). For a paramagnet having an effective moment |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
μeff, the Curie constant is written as |
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
0.02 |
|
|
|
|
|
|
Cp ¼ |
NApeff μB |
; |
|
|
|
|
(3) |
Molar |
|
|
|
|
|
|
|
||
3kB |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where NA is the molar concentration of ions and μB the |
|
|
|
|
|
|
|
|
|||||||||
Bohr |
magneton |
(μB=9.274×10−24 J/T). The effective |
|
0.00 |
|
|
|
|
|
|
|||||||
momentum number peff |
is defined as |
|
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
|||||||
|
|
|
|
Temperature (K) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
pefftheor |
¼ 2½SðS þ 1Þ&1=2; |
|
|
|
(4) |
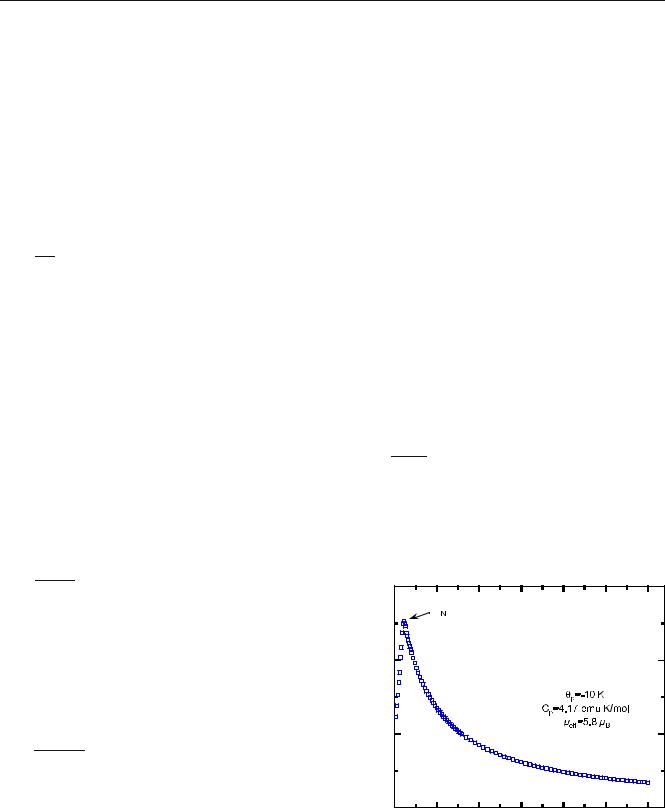
Fig. 2 Temperature dependence of the magnetic susceptibility of α- |
|||||||||||
|
|
|
NaFeO2 |
|
|
|
|
|
|
||||||||
