
Похилі перерізи
Якщо виріб має складну геометричну форму, то для виявлення конфігурації його окремих елементів будують похилий переріз.
При находженні істинного вигляду перерізу використовують один з способів нарисної геометрії: обертання, сполучення або зміни площин проекцій. Нижче описаний визначення істинного вигляду з використанням методу змінних площин проекцій.
Так як деталі складаються з геометричних тіл різної форми, то необхідно вивчити перерізи простих геометричних тіл.
Переріз прямого кругового циліндра. Відомо, що переріз прямого кругового циліндра площиною, яка похила до його вісі – це еліпс.
Розглянемо побудову проекцій і натурального розміру перерізу прямого кругового циліндра фронтально-проекціюючою площиною А—А. На рис. 41 є три проекції прямого кругового циліндра, вісь якого перпендикулярна горизонтальній площині проекцій. В результаті перерізу зовнішньої поверхні:
а) на фронтальній проекції перерізу зливається зі слідом площини А—А, проекція перерізу виявлена відрізком прямої В2С2, дорівнює великій вісі еліпса;
б) на горизонтальній – проекція перерізу зливається з горизонтальною проекцією кола циліндра;
в) на профільній проекції – еліпс будують як третю проекцію по двом даним (рис. 41).
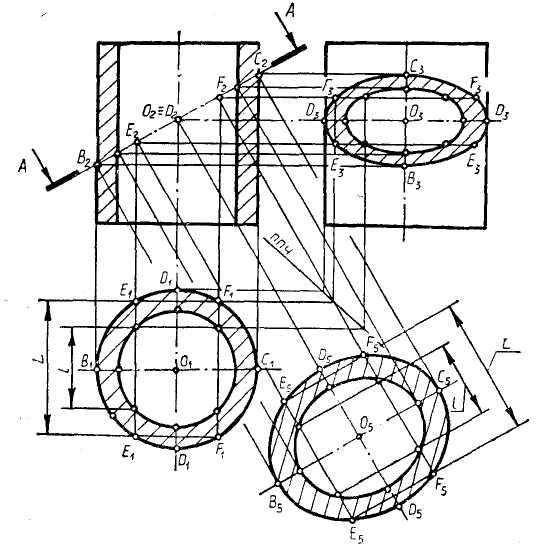
Рис. 41. Переріз циліндра похилою площиною.
Для побудови натурального перерізу замінимо дану горизонтальну площину проекцій (вигляд зверху) новою площиною. З цією метою проведемо в новій площині на вільному полі креслення паралельно лінії перерізу А—А вісь перерізу, що будується, яку назвемо базовою. Вона може зображати будь-яку горизонтальну лінію початкового вигляду зверху. Тому зручно, коли базова вісь являється віссю симетрії перерізу.
Будь-яка шукана точка перерізу (в даному випадку зовнішнього контуру) на новій горизонтальній проекції лежить на відповідній лінії зв’язку і визначеним чином розміщена відповідно вісі базової лінії. Точки В2, О2 і С2 в цьому випадку дають точки В1, О1 і С1, що лежать на базовій вісі. Відрізок B5C5 – це велика вісь еліпса. При заміні площини проекцій розміри проекцій перерізу вздовж лінії зв’язку залишаються постійними, тобто відрізок E5E5 дорівнює відрізку Е1Е1 (рис. 41), а відрізок F5F5 – відрізку F1F1 (для зручності симетричні точки позначені однаково). Діаметр циліндра завжди визначає малу вісь еліпса D5D5=D1D1. Переріз внутрішнього циліндра будують аналогічно.
Переріз прямого кругового конуса. Розглянемо побудову проекцій і натуральну величину перерізу прямого кругового конуса фронтально-проектуючою площиною А—А. На рис. 42 представлені три проекції прямого кругового конуса з віссю, перпендикулярної горизонтальної площини проекцій. Необхідно пам’ятати, що переріз прямого кругового конуса похилої площини – це еліпс.
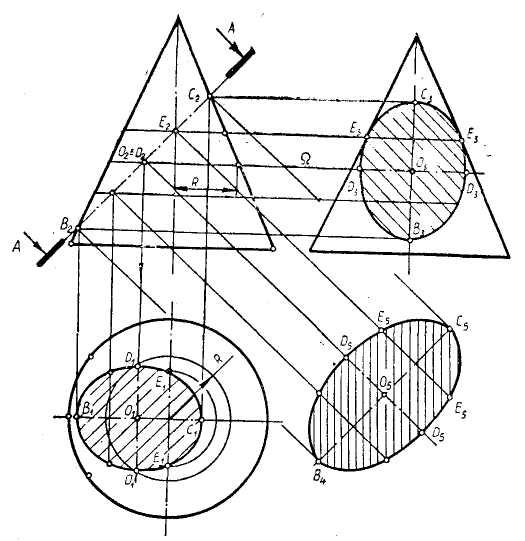 Рис.
42. Переріз конуса похилою площиною.
Рис.
42. Переріз конуса похилою площиною.
Якщо дана площина паралельна вісі, – це гіпербола. В розглянутому прикладі фронтальна проекція еліпса перерізу зливається з слідом січної площини А—А (відрізок С2В2 – велика вісь еліпса).
Для побудови
горизонтальної проекції еліпса необхідно
перед усім визначити проекції великої
і малої вісі і центра еліпса. Так як
центр еліпса ділить велику вісь навпіл,
то він лежить на середині відрізка С2В2
в точці
О2.
Тоді
горизонтальна проекція центра О1
знаходиться
на горизонтальній вісі конуса, а проекція
кінців великої вісі (точки В1
і С1)
– на
горизонтальній проекції контурних
утворюючих (співпадаючих з горизонтальною
віссю). Для побудови кінців малої вісі
(точок D1)
через
отриману точку О2
проводять
переріз горизонтальної площини
![]() (площина
рівня). Горизонтальна проекція цього
перерізу – коло радіуса R.
Переріз
отриманого кола і лінії зв’язку на
вигляді зверху визначає точки D1
–
проекції кінців малої вісі еліпса. Таким
же чином будують і інші точки, наприклад
точки Е1.
Побудова
натурального розміру перерізу конуса
аналогічно побудові натурального
розміру перерізу циліндра.
(площина
рівня). Горизонтальна проекція цього
перерізу – коло радіуса R.
Переріз
отриманого кола і лінії зв’язку на
вигляді зверху визначає точки D1
–
проекції кінців малої вісі еліпса. Таким
же чином будують і інші точки, наприклад
точки Е1.
Побудова
натурального розміру перерізу конуса
аналогічно побудові натурального
розміру перерізу циліндра.
Побудова похилого перерізу виробу складної геометричної форми. Можна рекомендувати наступний порядок побудови натурального розміру перерізу тіл складної геометричної форми (в якості приклада розглянемо виріб, що показаний на рис. 43).
Вивчить конфігурацію виробу і розбийте його на поверхні простої форми (циліндр, конус, призма та ін.), розглядаючи окремо зовнішню і внутрішню поверхні. На рис. 43, зовнішня поверхня – це шестигранна призма 1, яка переходить в циліндр 1; внутрішня – конус 1.
Виділіть ділянки пересікання січної площини з кожною поверхнею простої форми (ділянка В2Е2 для призми І, ділянка Е2С2 – для циліндра ІІ; ділянка N2T2 – для конусу 1).
Замінити площину проекції і для перерізу геометричного тіла симетричної форми провести базову вісь паралельно лінії перерізу; якщо ж задане геометричне тіло має несиметричну форму, то при побудові натурального розміру перерізу слід провести будь-яку базову лінію, від якої вже почніть будувати переріз. Так як розглянутий виріб має симетричну форму, то паралельно лінії А – А проведена базова вісь (вісь симетрії).
Використовуючи початкову горизонтальну проекцію (вид зверху), побудувати переріз натурального розміру на кожній окремій ділянці.
При відсутності достатнього досвіду окремі частини поверхні простої геометричної форми умовно доповніть штрихпунктирною лінією до лінії перерізу А – А і будувати їх повний натуральний розмір. Контури перерізу, доповнених частин показані штрихпунктирною лінією.
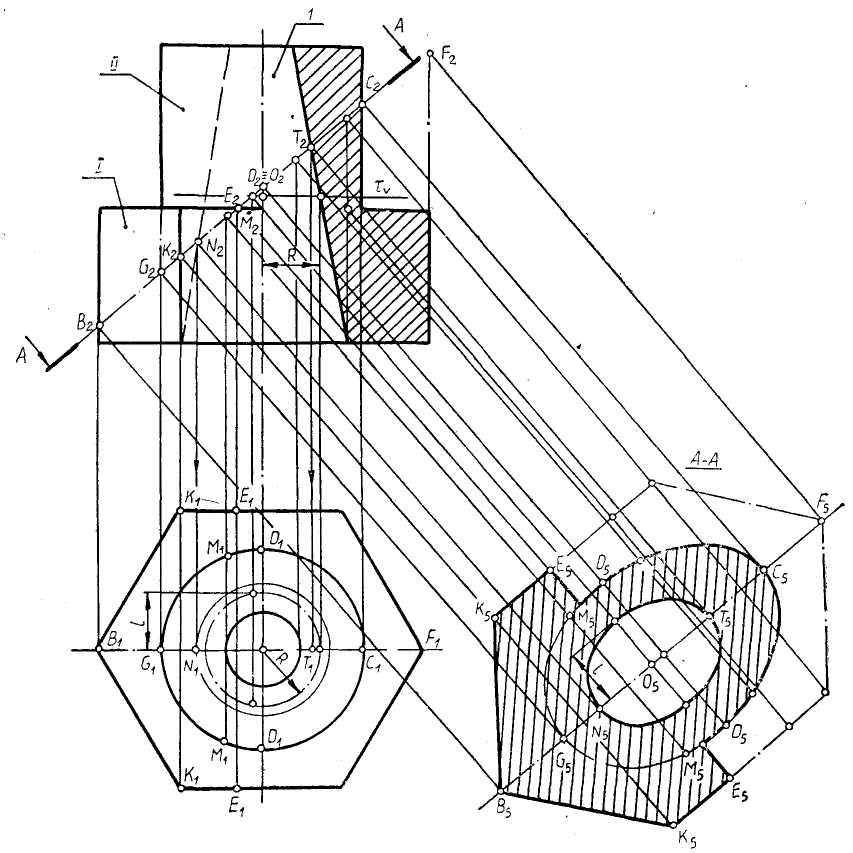
Рис. 43. Побудова похилого перерізу складної геометричної форми.
Розглянемо визначення натурального розміру перерізу поверхні шестигранної призми І. Доповнюємо призму штрихпунктирною лінією по висоті на ділянці E2F2 так, щоб січна площина А - А розділили повну бокову поверхню призми.
В результаті перерізу:
а) на фронтальній проекції перерізу B2F2 зливається зі слідом площини А – А;
б) на горизонтальній проекції перерізу зливається з горизонтальною проекцією поверхні призми.
При побудови натуральної величини перерізу необхідно враховувати, що розміри перерізу по лініям зв’язку залишаються при заміні площин проекцій незмінними, тобто K5K5=K1K1, E5E5 = E1E1. Додаткову частину перерізу призми, умовно показану на рис. 43 штрихпунктирною лінією, в основному контурі при побудові похилого перерізу на кресленнях не зображають.
Поверхню циліндра ІІ доповнюють на ділянці G2M2. Потім будують переріз повного циліндра по аналогії з рис. 41. Додаткову частину контуру перерізу циліндра M5G5M5 умовно показують штрихпунктирною лінією.
Внутрішній контур перерізу конічної поверхні виконують так, як це показано на рис. 42.
На рис. 44 представлено побудову істинного вигляду перерізу деталей площинами: фронтально-проекціюєчою А – А і горизонтально-проекціюєчою площиною Б – Б. В першому випадку для побудови істинного вигляду перерізу виконана заміна горизонтальної площини проекцій (вигляду зверху) на нову горизонтальну площину проекцій, а в другому – фронтальної площини проекцій (вигляд спереду) на нову фронтальну площину проекцій. Принцип побудови перерізу аналогічний попереднім прикладам.
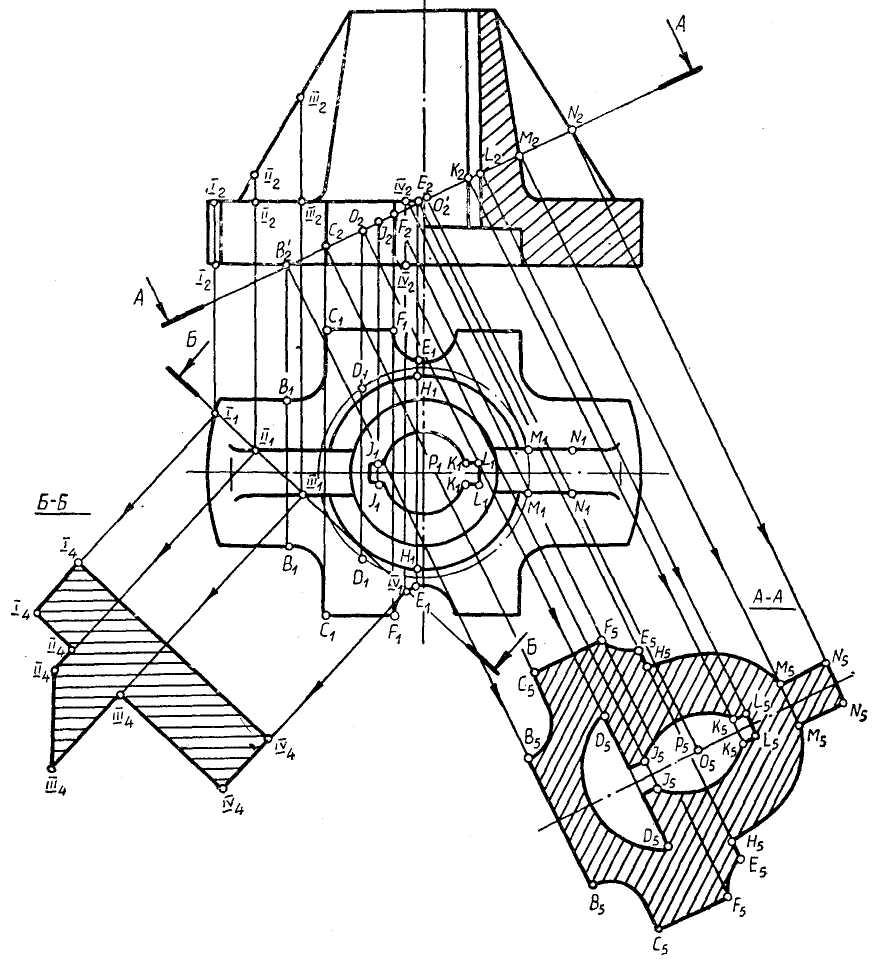
Рис. 44. Побудова істинного вигляду перерізу деталі, яка складається
з декількох геометричних поверхонь
Штриховку отриманих похилих перерізів виконують під кутом 45° до базової вісі або лінії перерізу, вона не паралельна штриховці основної деталі.
