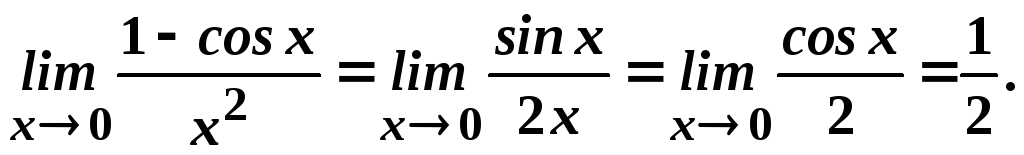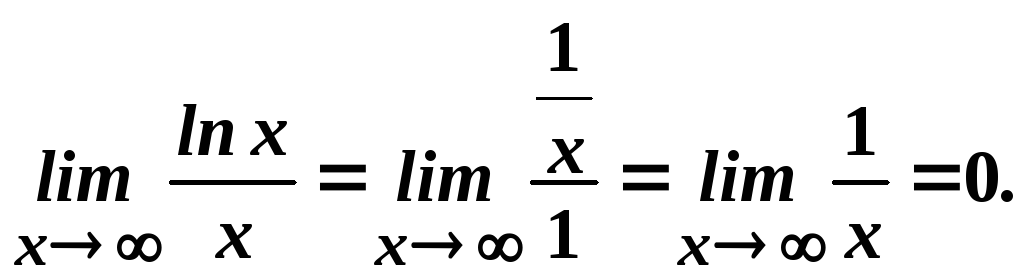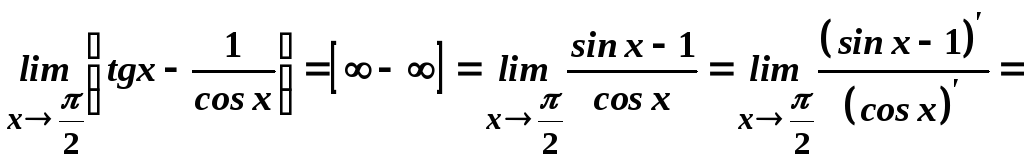- •1. Основні властивості неперервних функцій
- •1. Поняття рівномірної неперервності функції.
- •2. Теорема Кантора про рівномірну неперервність функції.
- •3. Теорема про неперервність оберненої функції.
- •Тема 5. Диференціальне числення функції однієї змінної
- •1. Задачі, що проводять до поняття похідної
- •Після спрощення одержуємо
- •2. Означення похідної
- •3. Механічний та геометричний зміст похідної
- •4. Односторонні похідні
- •5. Нескінченні похідні
- •1. Диференційовність функції
- •2. Похідні елементарних функцій
- •3. Похідна оберненої функції.
- •1. Диференціал функції
- •2. Похідні й диференціали вищих порядків
- •3. Формула Лейбніца для п-ної похідної добутку двох функцій.
- •4. Диференціали вищих порядків.
- •Тема 5. Застосування диференціального числення до дослідження функцій
- •1. Теореми про середнє значення
- •2. Теорема Ферма
- •3. Теорема Ролля
- •4. Теорема Лагранжа
- •5. Теорема Коші
- •1. Розкриття невизначеностей. Правило Лопіталя.
- •2. Застосування правила Лопіталя при розкритті невизначеностей вигляду .
- •1. Формула Тейлора для многочлена. Розглянемо многочлен
- •6.2. Формула Тейлора для довільної функції
- •Звідси одержуємо:
- •1. Ознака монотонності функції
- •3. Необхідні й достатні умови існування екстремуми функції
- •Достатні умови існування екстремуму функції.
- •1. Опуклість та вгнутість кривої. Точки перегину
- •2. Асимптоти графіка функції
- •3. Загальна схема дослідження функцій і побудови їх графіків
- •Тема 7. Інтеграл ньютоналейбніца
- •1. Поняття первісної функції та невизначеного інтеграла
- •2. Основні властивості невизначеного інтеграла
- •3. Таблиця основних інтегралів
- •1. Подання раціональних дробів у вигляді суми найпростіших дробів
- •2. Інтегрування найпростіших раціональних дробів
- •1. Інтегрування ірраціональних функцій
- •Інтегрування деяких тригонометричних функцій
- •Приклади
1. Розкриття невизначеностей. Правило Лопіталя.
Теорема 1 ( правило Лопіталя).Нехай
функції![]() і
і![]() визначені в проміжку
визначені в проміжку![]() і
і![]() .
Нехай, крім того, в проміжку
.
Нехай, крім того, в проміжку![]() існують скінченні похідні
існують скінченні похідні![]() і
і![]() ,
причому
,
причому![]() .
Тоді, якщо існує границя
.
Тоді, якщо існує границя ,
то існує й границя
,
то існує й границя ,
причому
,
причому
 .
.
Доведення.Доозначимо в точці![]() функції
функції![]() і
і![]() ,
поклавши
,
поклавши![]() .
Тоді на відрізку
.
Тоді на відрізку![]() функції
функції![]() і
і![]() задовольняють умовам теореми Коші.
Отже,
задовольняють умовам теореми Коші.
Отже,
 ,
,
де
![]() .
Якщо
.
Якщо![]() ,
то зрозуміло, що й
,
то зрозуміло, що й![]() .
Враховуючи, що
.
Враховуючи, що![]() і те, що існує границя
і те, що існує границя ,
робимо висновок
,
робимо висновок
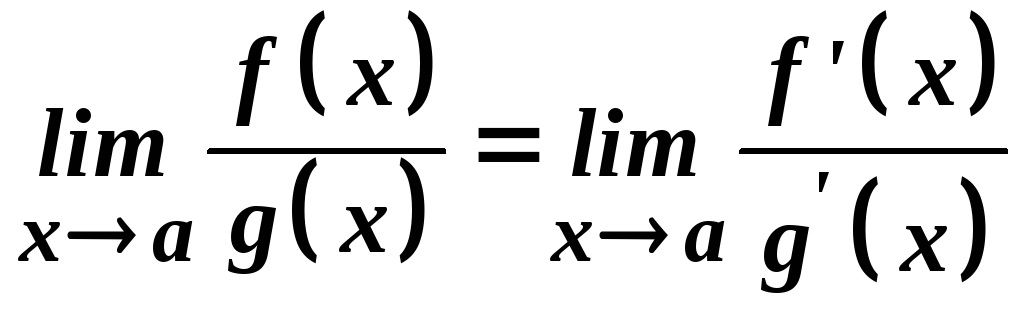 .
.
Зауваження.Якщо похідні![]() і
і![]() задовольняють умовам, котрі накладаються
в наведеній теоремі на функції
задовольняють умовам, котрі накладаються
в наведеній теоремі на функції![]() і
і![]() ,
то правило Лопіталя можна застосувати
повторно, тобто
,
то правило Лопіталя можна застосувати
повторно, тобто
 .
.
Теорема 1 справджується й тоді, коли
![]() .
Нехай функції
.
Нехай функції![]() і
і![]() визначені в проміжку
визначені в проміжку![]() ,
,![]() ,
і в проміжку
,
і в проміжку![]() існують скінчені похідні
існують скінчені похідні![]() та
та![]() ,
де
,
де![]() .
Тоді, якщо існує границя
.
Тоді, якщо існує границя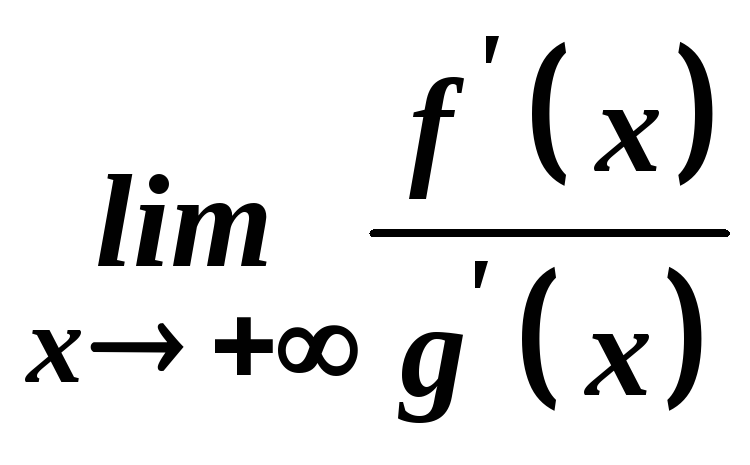 ,
то існує й границя
,
то існує й границя ,
причому
,
причому
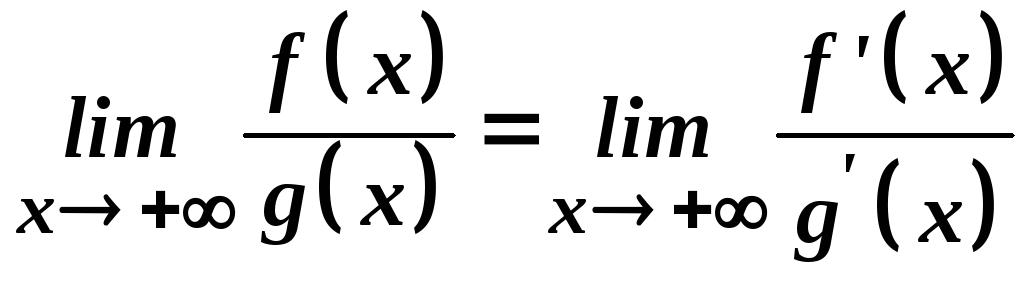 .
.
Для доведення цього твердження достатньо
покласти
![]() і застосувати теорему 1.
і застосувати теорему 1.
Теорема 2
(правило Лопіталя).Нехай функції![]() і
і![]() визначені в проміжку
визначені в проміжку![]() ,
,![]() і в проміжку
і в проміжку![]() існують скінчені похідні
існують скінчені похідні![]() та
та![]() ,
причому
,
причому![]() .
Тоді, якщо існує границя
.
Тоді, якщо існує границя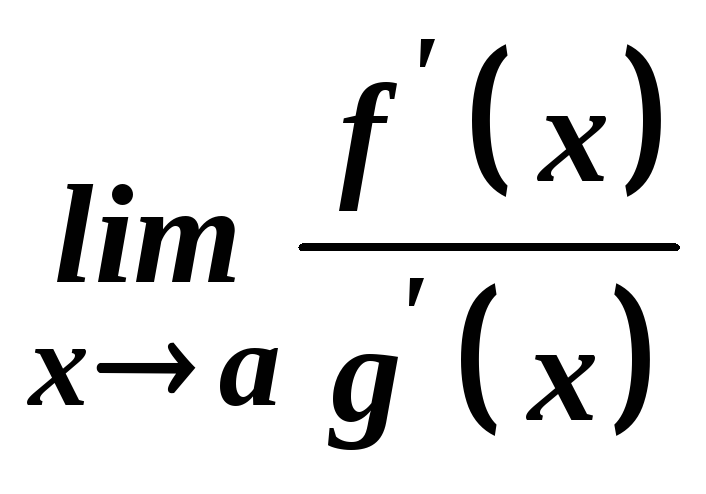 ,
то існує й границя
,
то існує й границя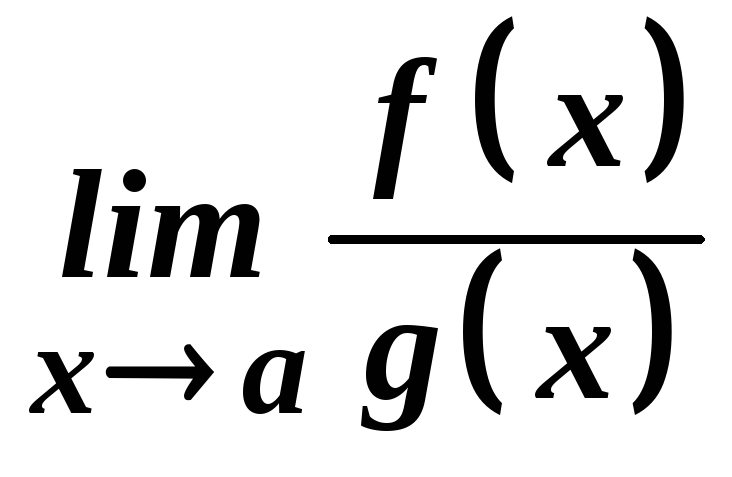 ,
причому
,
причому
 .
.
Доведення
цієї теореми можна прочитати, наприклад,
в книзі Г. М. Фихтенгольца “Основы
математического анализа”, т. 1. М.: Наука, 1964. Теорема 2 має місце також,
коли![]() .
.
Правило
Лопіталя дає можливість розкривати
невизначеності типу
![]() .
.
Приклади.
2. Застосування правила Лопіталя при розкритті невизначеностей вигляду .
Правило Лопіталя можна застосовувати
при розкритті невизначеностей вигляду
![]() .
.
Приклади.
![]() .
.
 .
.
 .
.

Знайдемо
 .
.
Отже,
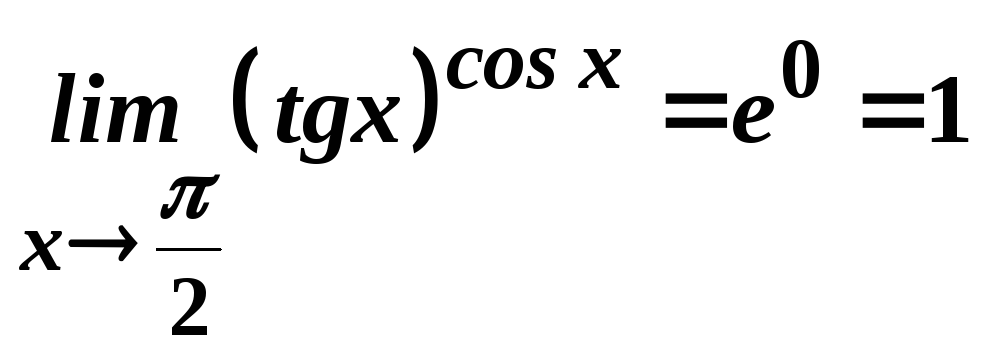 .
.
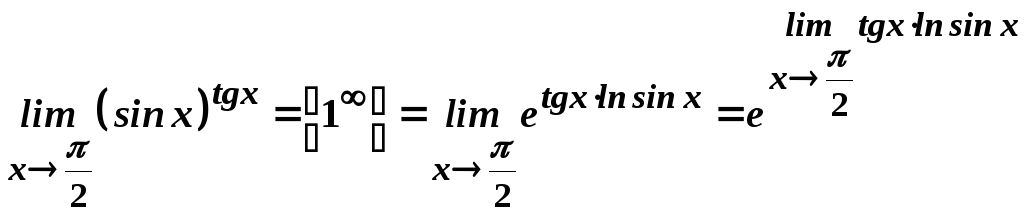 .
.
Знайдемо
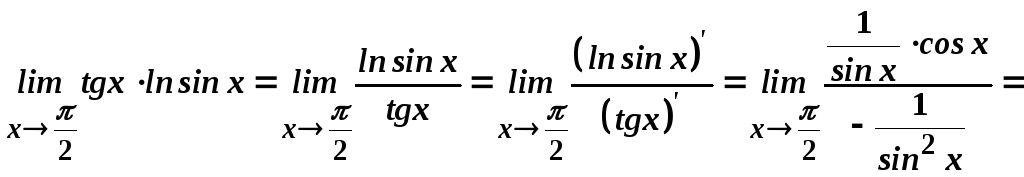
 .
.
Отже,
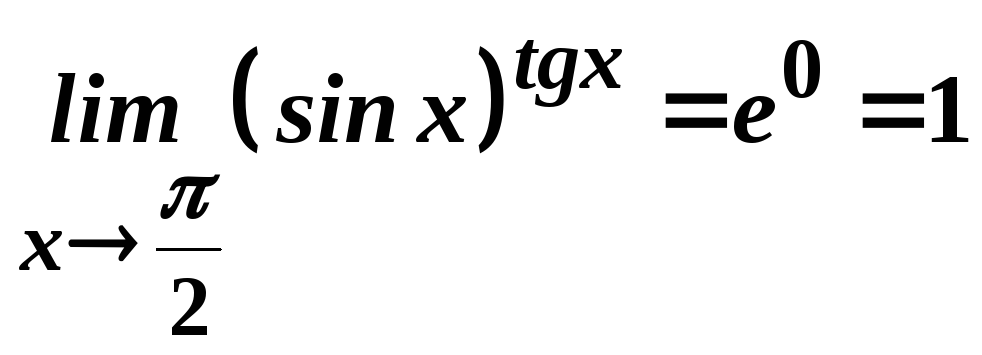 .
.
ЛЕКЦІЯ 20
Формула Тейлора для многочлена.
Формула Тейлора для довільної функції.
1. Формула Тейлора для многочлена. Розглянемо многочлен
![]() ,
,
де
![]() дійсні числа.
Продиференціюємо многочлен
дійсні числа.
Продиференціюємо многочлен![]()
![]() раз.
раз.

Якщо в наведених формулах покласти
![]() ,
то одержимо
,
то одержимо


Отже, можна записати
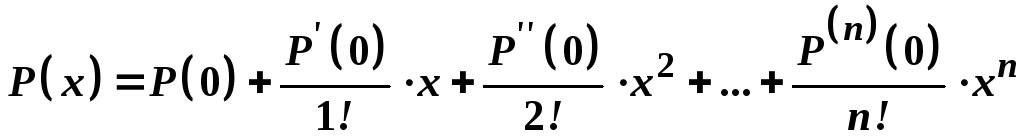 (1)
(1)
Нехай маємо многочлен
![]() за степенями
за степенями![]() ,
де
,
де![]() деяке стале дійсне число, тобто
деяке стале дійсне число, тобто
![]() ,
,
де
![]() дійсні числа.
Поклавши
дійсні числа.
Поклавши![]() ,
матимемо
,
матимемо
![]() .
.
Звідси аналогічно до попереднього, одержимо
 (2)
(2)
Формула (1) є окремим випадком (![]() )
формули (2). Кожну із цих формул називають
формулою Тейлора. Формулу (1) інакше
називають формулою Маклорена.
)
формули (2). Кожну із цих формул називають
формулою Тейлора. Формулу (1) інакше
називають формулою Маклорена.
6.2. Формула Тейлора для довільної функції
Теорема
Тейлора. Нехай функція![]() в точці
в точці![]() і в деякому її околі має похідні
і в деякому її околі має похідні![]() -
го порядку. Нехай також
-
го порядку. Нехай також![]() деяка точка, що належить околу, про який
йде мова. Тоді існує точка
деяка точка, що належить околу, про який
йде мова. Тоді існує точка![]() ,
яка лежить між точками
,
яка лежить між точками![]() і
і![]() ,
така, що
,
така, що
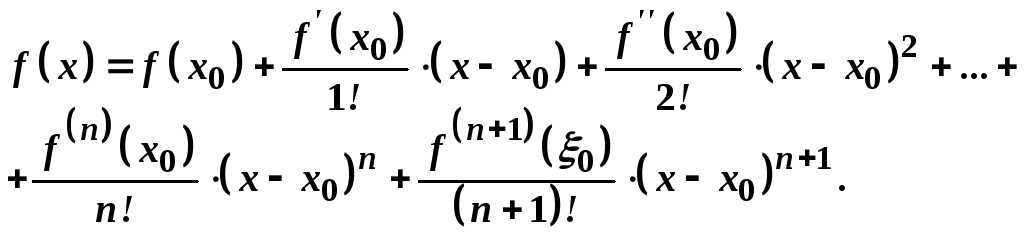 (3)
(3)
Доведення.Позначимо

Покладемо
![]()
Покажемо, що існує точка
![]() така, що
така, що
 .
.
Зафіксуємо довільну точку
![]() із вказаного околу точки
із вказаного околу точки![]() .
Для визначеності уважатимемо, що
.
Для визначеності уважатимемо, що![]() .
Нехай
.
Нехай![]() змінна, яка пробігає значення відрізку
змінна, яка пробігає значення відрізку
![]() .
Складемо допоміжну функцію
.
Складемо допоміжну функцію
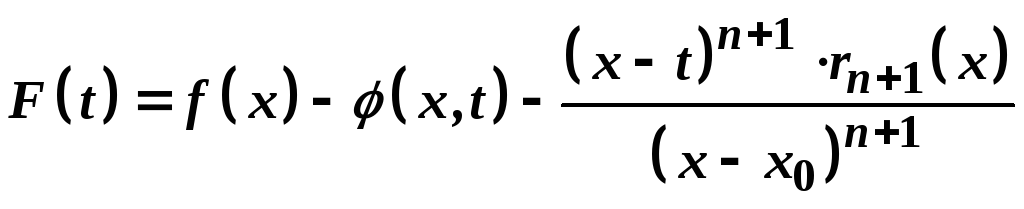 .
.
Функція
![]() на відрізку
на відрізку
![]() задовольняє всім умовам теореми Ролля:
задовольняє всім умовам теореми Ролля:
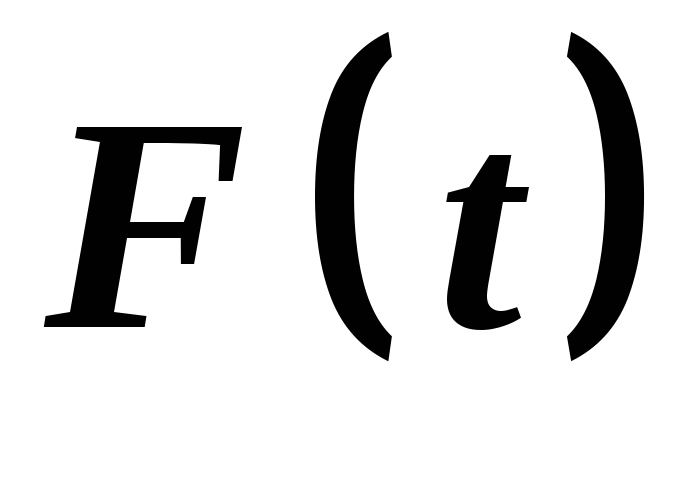 неперервна на
неперервна на
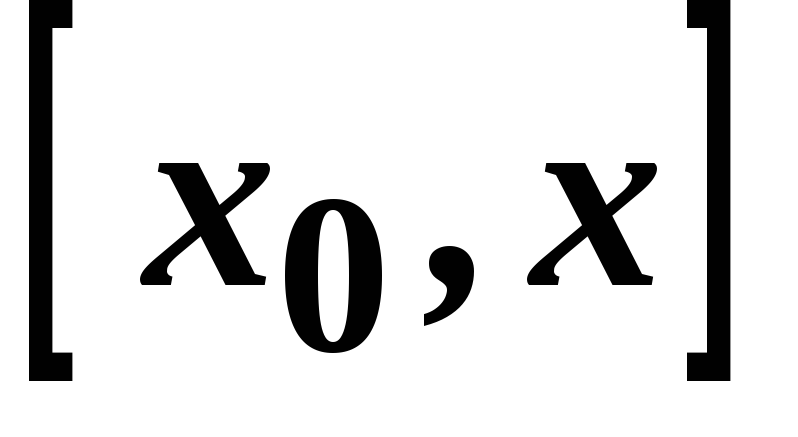 ,
, диференційована на
диференційована на
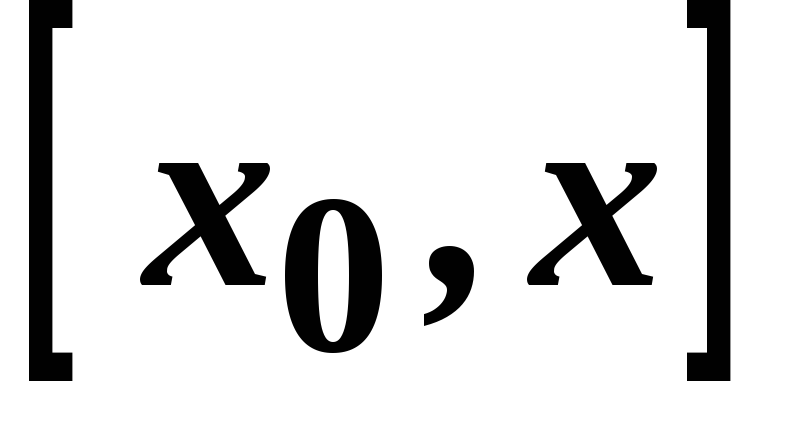 ,
,
(
ці властивості функції ![]() випливають із умов, накладених на функцію
випливають із умов, накладених на функцію![]() )
)
на кінцях відрізка
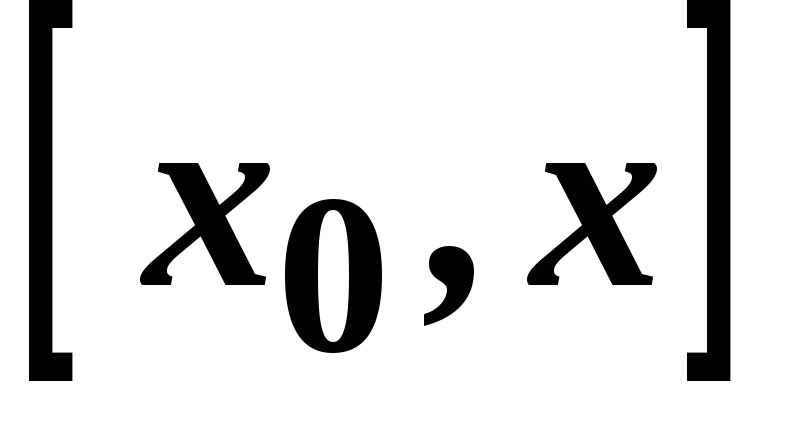 функція
функція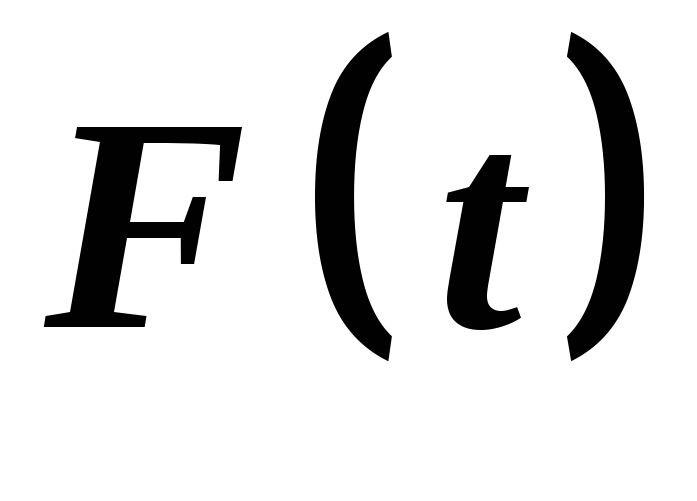 має рівні значення. Дійсно
має рівні значення. Дійсно
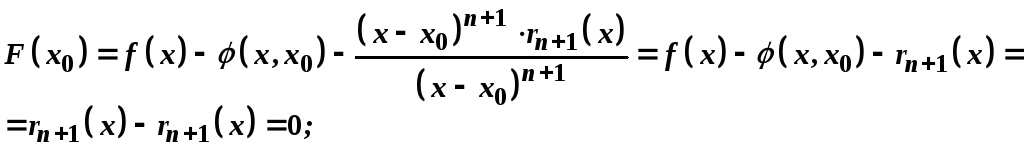

Отже,
за теоремою Ролля існує точка![]() така, що
така, що![]() .
Знайдемо
.
Знайдемо![]() .
.
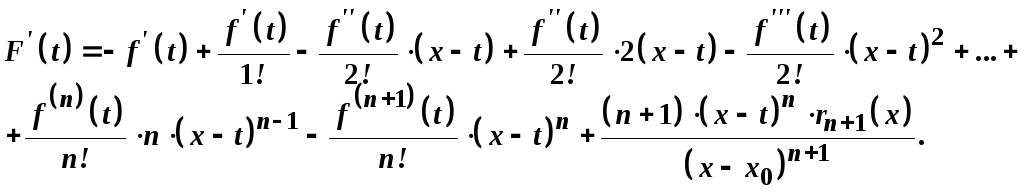
Оскільки в правій частині одержаної формули знищуються всі члени, за виключенням двох останніх, то
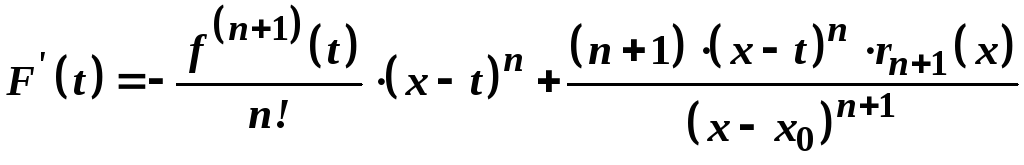 .
.
Далі маємо:
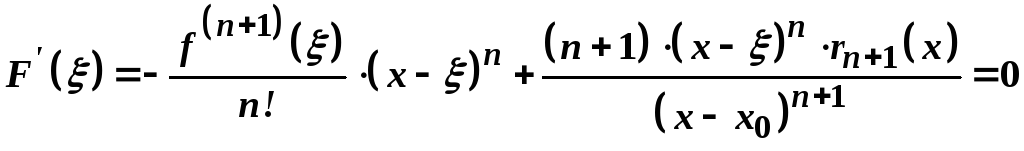 .
.