3. Теорема Ролля

Теорема. Якщо функціявизначена на відрізкуі вона

1. неперервна в кожній точці відрізка .

2. диференційована на інтервалі .

3. на кінцях відрізка приймає рівні значення,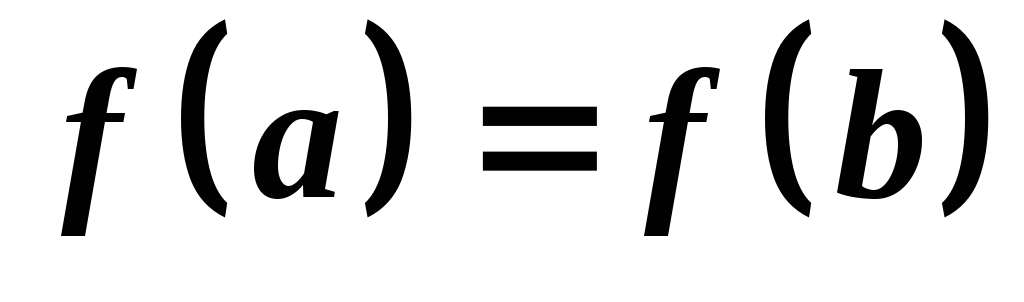

то існує точка така, що.

Доведення. Оскільки функціянеперервна на відрізку, то за другою теоремою Вейєрштрасса існують точки, в яких функція приймає найменшеі найбільшезначення, тобтоі.

Якщо , то функціяна відрізкуприймає постійне значення, оскільки. Томув будь-якій точці інтервалу.

Якщо , то принаймні одне із значеньабофункція приймає у деякій точці, тобто на кінцях відрізка( оскільки).

Так як функція диференційована в точці, то за теоремою Ферма.

Із теореми Ролля випливає, що для функції неперервної на відрізку, диференційованої на інтерваліі такої, що, існує точкатака, що дотична до графіка функціїу точціпаралельна вісі(рис. 23).

4. Теорема Лагранжа

Якщо функція визначена на відрізкуі вона

1. неперервна в кожній точці відрізка ,

2. диференційована на інтервалі , то існує точкатака, що

.

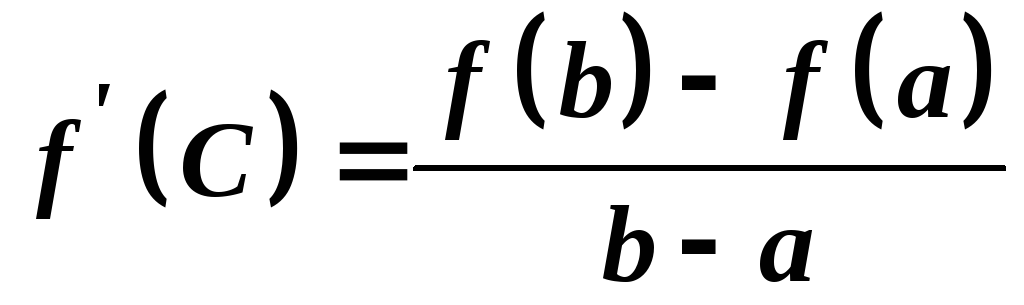Доведення.Розглянемо допоміжну функцію

.

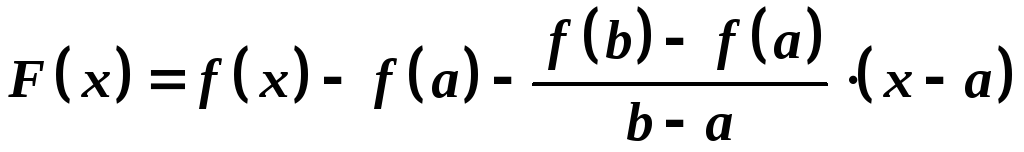Ця функція визначена на відрізку і задовольняє всім умовам теореми Ролля. Дійсно,

1. оскільки 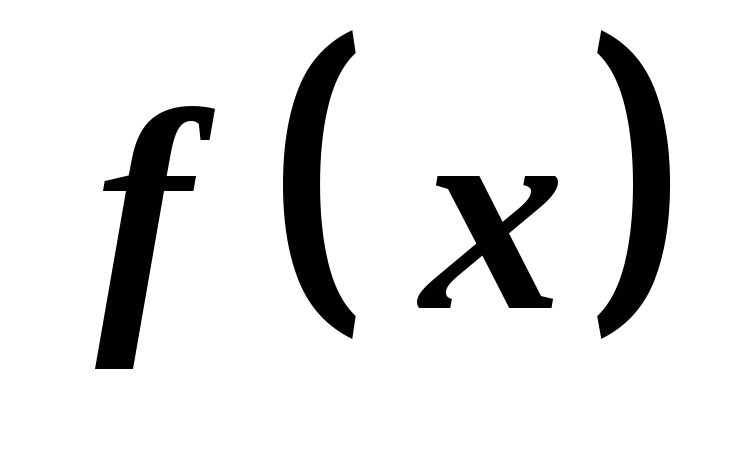інеперервні функції на відрізку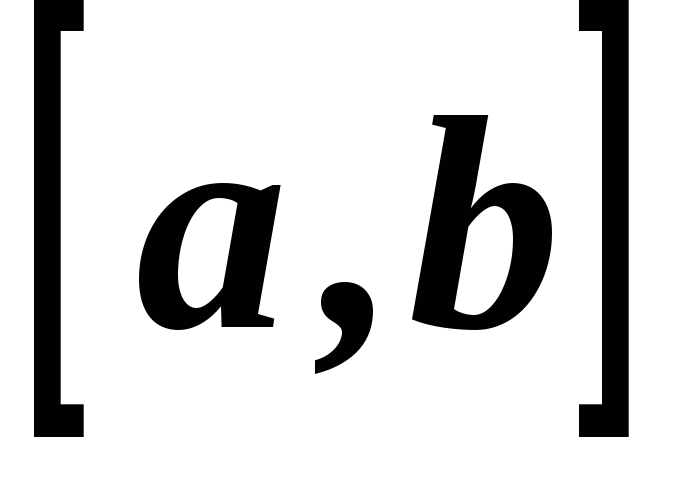, то і функція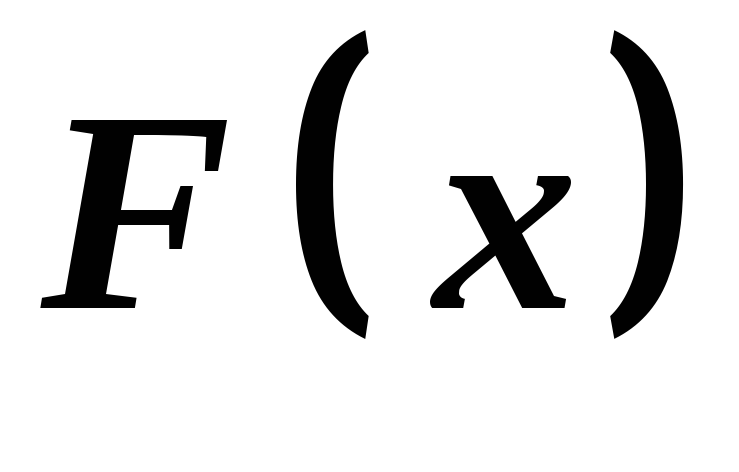також неперервна на.

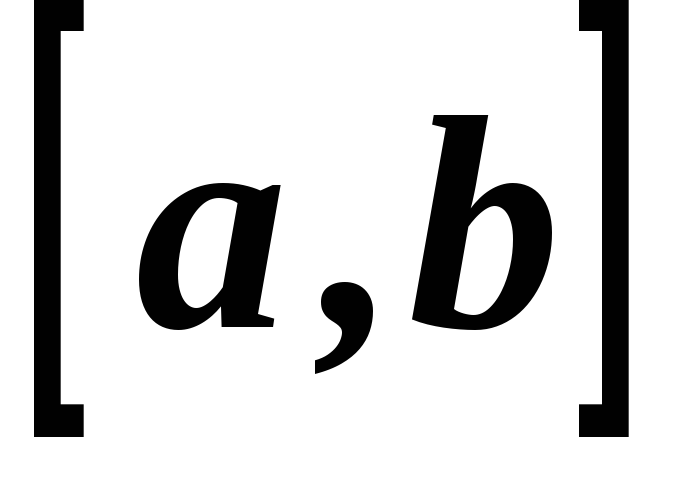2. функція диференційована на інтервалі:

.

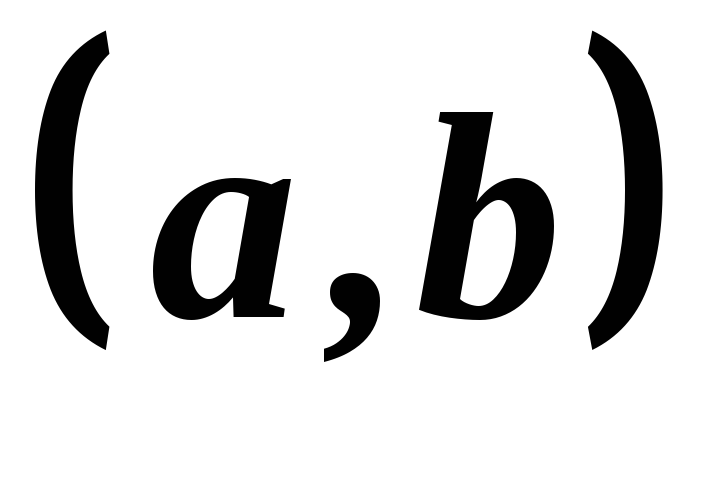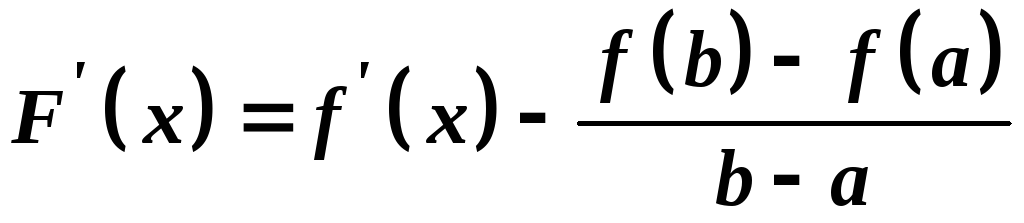3. на кінцях відрізку функціямає рівні значення

.

За теоремою Ролля існує точка така, що, тобто

.

Звідси маємо

.

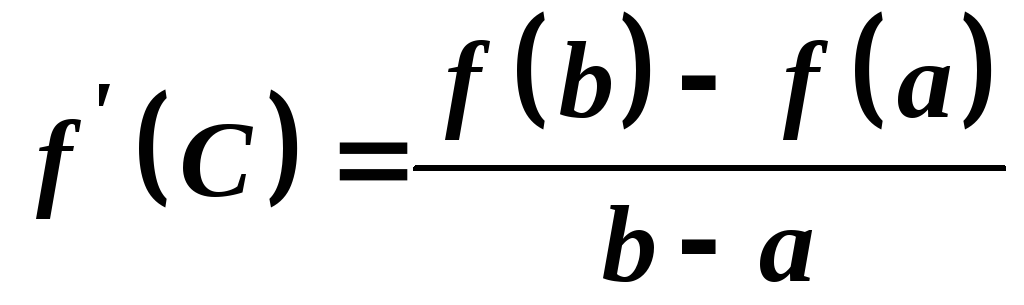Зауваження.Якщо функціяна відрізкузадовольняє умовам теореми Лагранжа, то із останньої формули одержуємо

.

Ця формула називається формулою скінчених приростів або формулою Лагранжа. Якщо в цій формулі покласти , то одержимо

, де.

Геометричний зміст теореми Лагранжа полягає в наступному. Якщо функція задовольняє умовам теореми Лагранжа, то існує точкатака, що дотична до графіка функціїу точціпаралельна хорді, проведеній через точки(рис. 24).

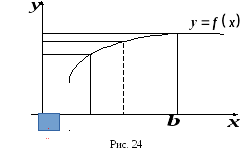
Наслідки з теореми Лагранжа.

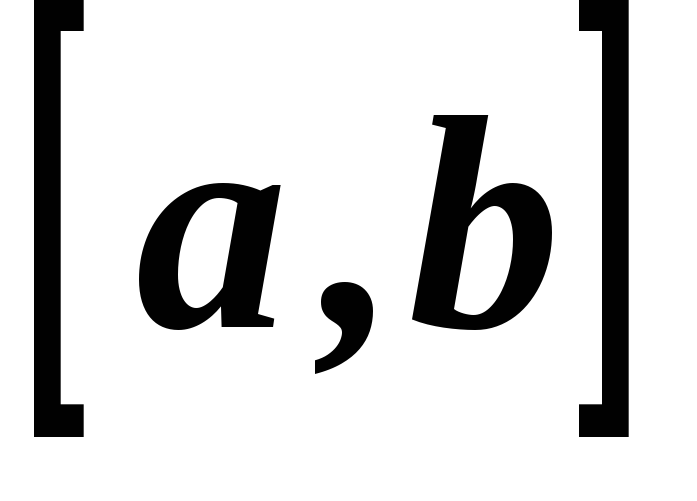
1. Якщо функція на відрізку, має похідну, то на відрізкустала.

Враховуючи, що похідна від сталої функції дорівнює нулю, що було установлено раніше, і сформульований щойно наслідок. можна сформулювати критерій сталості диференційованої на заданому проміжку функції:

Для того, щоб функція , диференційована на проміжку, була сталою, необхідно і достатньо, щоб її похіднабула рівною нулю в усіх точках цього проміжку.

3. Якщо функці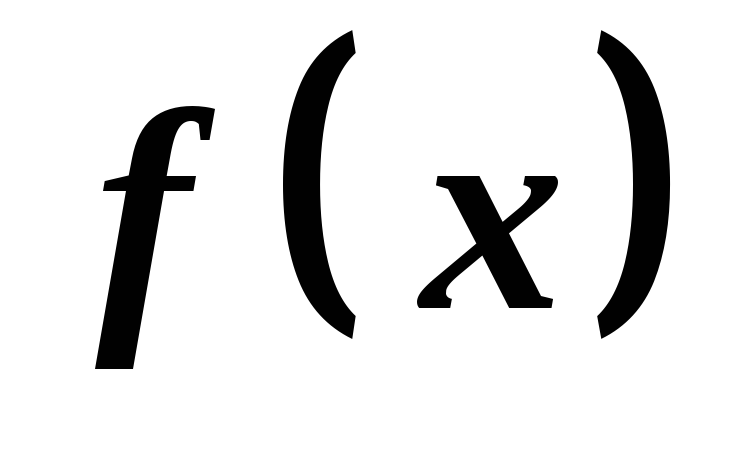ї інеперервні на проміжку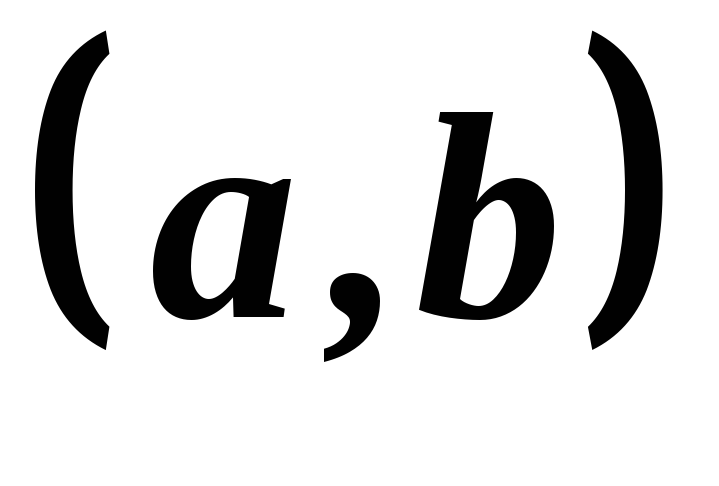і при будь-якому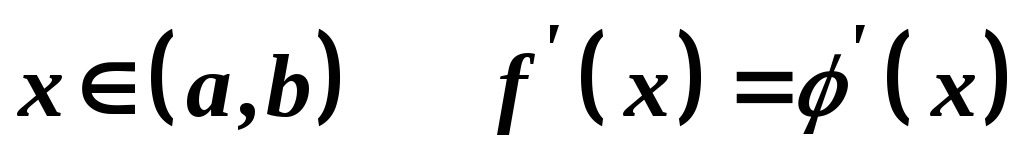, то функціяє сталою, тобто, де.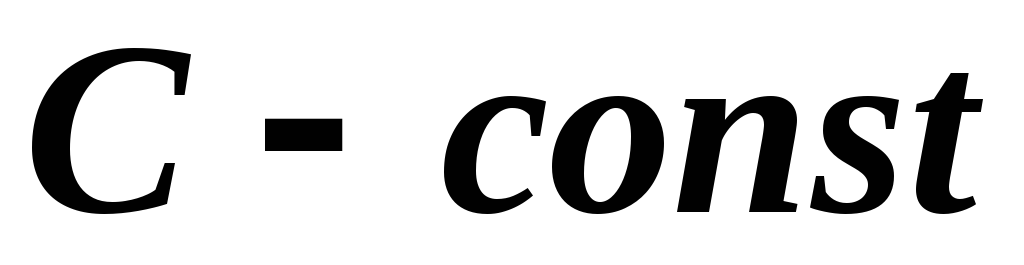

5. Теорема Коші

Теорема. Якщо функціїі1) неперервні на відрізку,

2) диференційовані на інтервалі , і,

то існує точка така, що.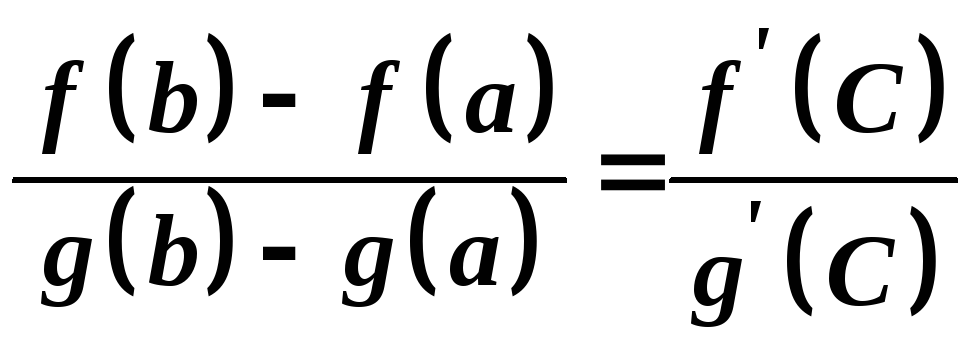

Доведення.Побудуємо допоміжну функцію

.

Легко перевірити, що ця функція задовольняє всім умовам теореми Ролля: неперервна на, диференційована наі. Отже, за теоремою Ролля існує точкатака, що. Оскільки

,

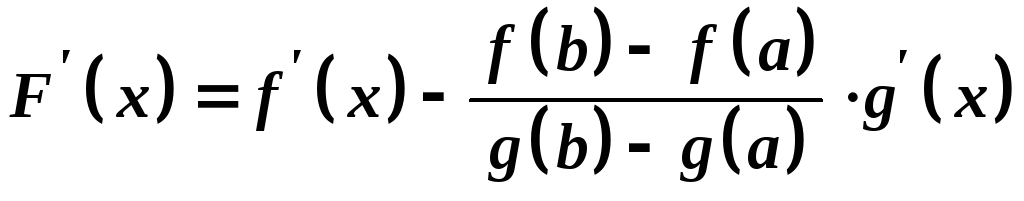то

.

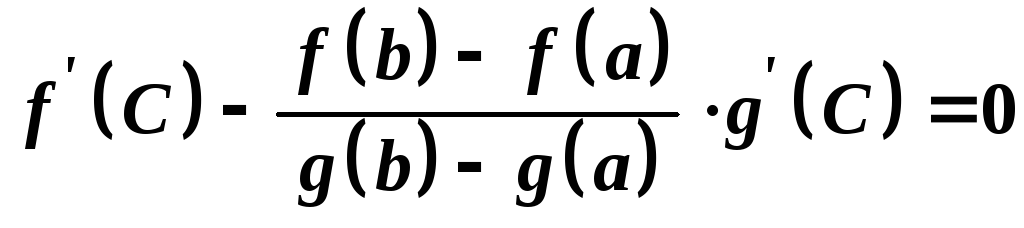Звідси маємо

.

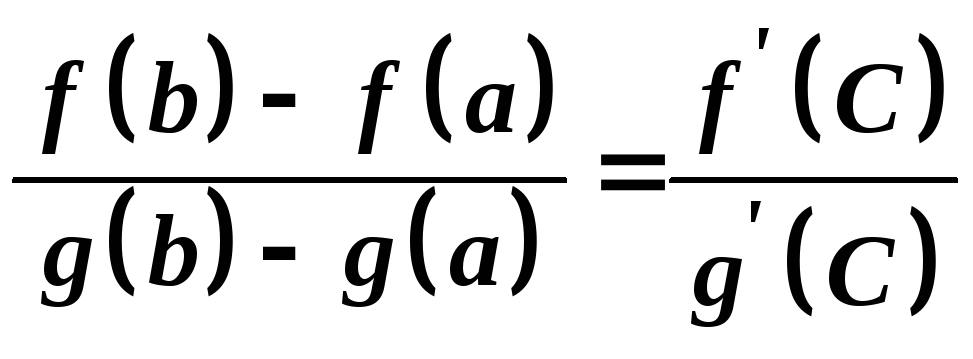Одержана формула називається формулою Коші або узагальненою формулою скінчених приростів.

Зауваження.У формулі Кошітому, що за умови, згідно з теоремою Ролля існувала б точкатака, що, що суперечить умові.

ЛЕКЦІЯ 19

22. Розкриття невизначеностей. Правило Лопіталя.

2.Застосування правила Лопіталя при розкритті невизначеностей вигляду .