1. Подання раціональних дробів у вигляді суми найпростіших дробів

Розглянемо дробово-раціональну функцію , де

многочлен n-го степеня, амногочленk-го степеня. Якщо n k, то, виконавши ділення, одержимо

,

де r < k. Наприклад,

.

У вищій алгебрі доводиться, що кожний многочлен можна подати у вигляді добутку

, (1)

де Акоефіцієнт при старшому членові многочлена, акорені рівняння= 0. Множникиназиваються елементарними. Якщо серед них є однакові, то групуючи їх, одержимо

, (2)

де . Числаназиваються кратностями коренів. Серед коренівможуть бути й комплексні. Якщоr-кратний комплексний корінь многочлена з дійсними коефіцієнтами, то цей многочлен має також спряжений зr-кратний корінь . Отже, якщо формула (2) містить множник, де, то вона також містить і множник. Перемноживши ці множники, одержимо

=,

де ,, p, qдійсні числа.

Ураховуючи всі комплексні корені многочлена , формулу (2) можна записати у вигляді

,

де дійсні числа.

Дріб , де r < n називається правильним раціональним дробом.

Теорема.Правильний раціональний дріб, де

можна єдиним чином подати у вигляді суми найпростіших дробів

,

де дійсні числа.

Подання, про яке йдеться у наведеній теоремі, можна виконати методом невизначених коефіцієнтів, котрий розглянемо на наступному прикладі.

Приклад.Розкласти на найпростіші дроби

.

Розв’язування. Згідно з наведеною теоремою маємо:

,

де поки що невідомі числа.

Зведемо праву частину останньої рівності до спільного знаменника.

Два многочлени тотожно рівні між собою тоді й тільки тоді, коли рівні між собою коефіцієнти при однакових степенях х. Тому для визначення коефіцієнтівскладемо систему

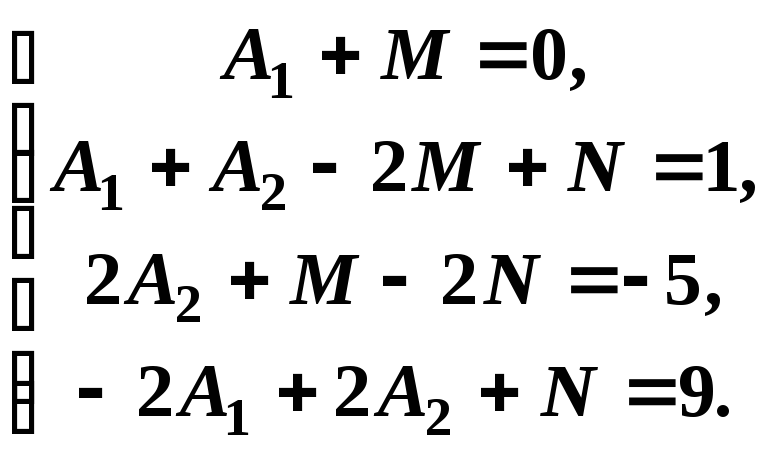
Розв’язавши цю систему, одержимо:

.

Отже,

.

2. Інтегрування найпростіших раціональних дробів

Розглянемо інтеграли від найпростіших ірраціональних дробів.

1. .

2..

3..

Тут многочлен не має дійсних коренів , отже. Виділимо повний квадрат

.

Уведемо підстановку . Тоді. Далі покладемо. Маємо:

.

Перший із інтегралів правої частині, обчислюється безпосередньо

.

Другий інтеграл обчислюється за формулою 4) таблиці основних інтегралів.

36. .

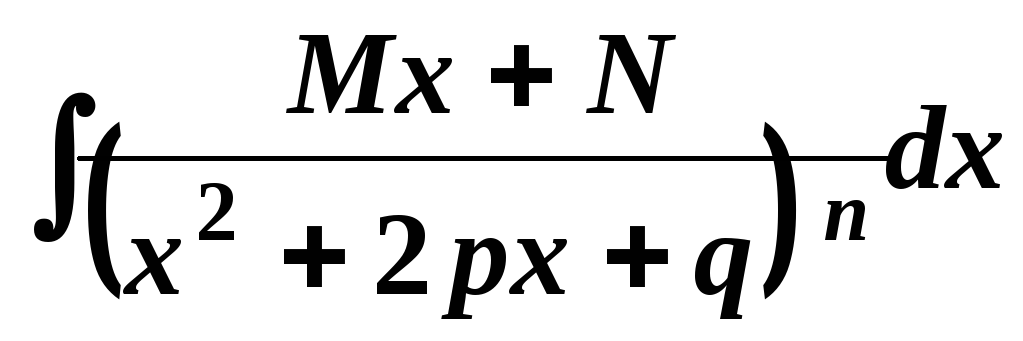Увівши підстановку , одержимо. Покладемо. Тоді

.

Перший із інтегралів правої частини легко зводиться до інтегралу 1) таблиці основних інтегралів, а другий інтеграл

обчислюється за рекурентною формулою

.

ЛЕКЦІЯ 25

37. Інтегрування ірраціональних функцій.

38. Інтегрування деяких тригонометричних функцій.

1. Інтегрування ірраціональних функцій

Інтеграл від ірраціональної функції не завжди обчислюється в

скінченному вигляді. Проте деякі типи таких інтегралів за допомогою певних підстановок можна звести до інтегралів від раціональних функцій.

Позначимо раціональну функцію від змінних. Наприклад, функціяє раціональною від, тобто

.

Інтеграли виду ,

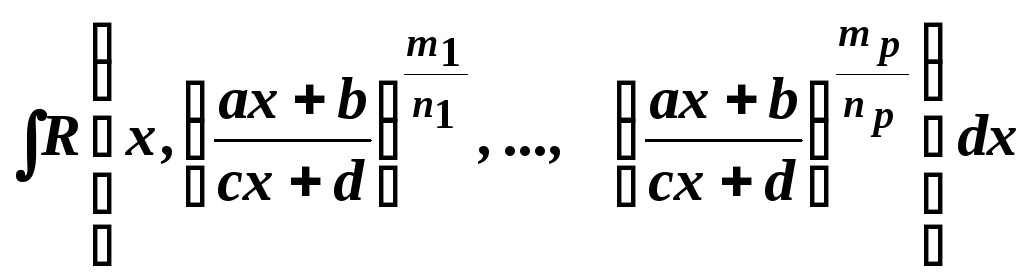де натуральні числа,дійсні числа, причому(у іншому випадкустала величина) обчислюється за допомогою введення нової змінної

,

де kспільний знаменник дробів.

Приклад 1. Обчислити.

Розв’язування. Зробимо підстановку . Одержимо

.

Далі маємо

.

Приклад 2. Обчислити.

Розв’язування.

.

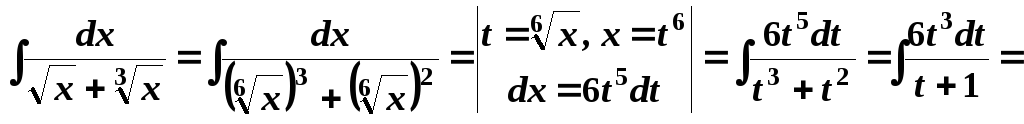
Інтеграли виду зводяться до інтегралів від раціональних функцій за допомогою підстановок Ейлера.

Якщо , то вводиться нова зміннаt :

,

де знаки можна брати у будь-якій послідовності.

Якщо у тричлені , то можна використати іншу підстановку

.

У випадку коли і тричлен має дійсні різні кореній, то використовується підстановка

або

.

Зазначимо, що підстановки Ейлера часто приводять до досить складних раціональних функцій, а тому на практиці при обчисленні інтегралів цього типу користуються простішими методами.