
- •1. Основні властивості неперервних функцій
- •1. Поняття рівномірної неперервності функції.
- •2. Теорема Кантора про рівномірну неперервність функції.
- •3. Теорема про неперервність оберненої функції.
- •Тема 5. Диференціальне числення функції однієї змінної
- •1. Задачі, що проводять до поняття похідної
- •Після спрощення одержуємо
- •2. Означення похідної
- •3. Механічний та геометричний зміст похідної
- •4. Односторонні похідні
- •5. Нескінченні похідні
- •1. Диференційовність функції
- •2. Похідні елементарних функцій
- •3. Похідна оберненої функції.
- •1. Диференціал функції
- •2. Похідні й диференціали вищих порядків
- •3. Формула Лейбніца для п-ної похідної добутку двох функцій.
- •4. Диференціали вищих порядків.
- •Тема 5. Застосування диференціального числення до дослідження функцій
- •1. Теореми про середнє значення
- •2. Теорема Ферма
- •3. Теорема Ролля
- •4. Теорема Лагранжа
- •5. Теорема Коші
- •1. Розкриття невизначеностей. Правило Лопіталя.
- •2. Застосування правила Лопіталя при розкритті невизначеностей вигляду .
- •1. Формула Тейлора для многочлена. Розглянемо многочлен
- •6.2. Формула Тейлора для довільної функції
- •Звідси одержуємо:
- •1. Ознака монотонності функції
- •3. Необхідні й достатні умови існування екстремуми функції
- •Достатні умови існування екстремуму функції.
- •1. Опуклість та вгнутість кривої. Точки перегину
- •2. Асимптоти графіка функції
- •3. Загальна схема дослідження функцій і побудови їх графіків
- •Тема 7. Інтеграл ньютоналейбніца
- •1. Поняття первісної функції та невизначеного інтеграла
- •2. Основні властивості невизначеного інтеграла
- •3. Таблиця основних інтегралів
- •1. Подання раціональних дробів у вигляді суми найпростіших дробів
- •2. Інтегрування найпростіших раціональних дробів
- •1. Інтегрування ірраціональних функцій
- •Інтегрування деяких тригонометричних функцій
- •Приклади
Тема 7. Інтеграл ньютоналейбніца
ЛЕКЦІЯ 23
Поняття первісної функції та невизначеного інтеграла.
Основні властивості невизначеного інтеграла.
Таблиця основних інтегралів.
Безпосереднє інтегрування.
Метод підстановки.
Інтегрування частинами.
1. Поняття первісної функції та невизначеного інтеграла
Однією із основних задач диференціального
числення є знаходження похідної![]()
![]() заданої функції
заданої функції![]() .
Різноманітні питання математичного
аналізу і його застосувань приводять
до оберненої задачі: для даної функції
.
Різноманітні питання математичного
аналізу і його застосувань приводять
до оберненої задачі: для даної функції![]() знайти таку функцію
знайти таку функцію![]() ,
похідна якої рівна
,
похідна якої рівна![]() ,
тобто
,
тобто![]() =
=![]() .
.
Відтворення функції за відомою її похідною одна із основних задач інтегрального числення.
Функція
![]() називається первісною для функції
називається первісною для функції![]() ,
на деякому проміжкуХ, якщо для
усіх значеньх Хвиконується рівність
,
на деякому проміжкуХ, якщо для
усіх значеньх Хвиконується рівність![]() =
=![]() .
.
Якщо
![]() первісна для функції
первісна для функції![]() ,
то й функція
,
то й функція![]() ,
деС довільна стала, також є первісною для
функції
,
деС довільна стала, також є первісною для
функції![]() ,
оскільки(
,
оскільки(![]() )′=
)′=![]() +
С ′=
+
С ′= ![]() + 0 =
+ 0 =![]() .
.
Нехай первісною функції
![]() на проміжкуХ, крім функції
на проміжкуХ, крім функції![]() ,
є функція
,
є функція![]() ,
тобто
,
тобто![]() =
=![]() .
Розглянемо різницю
.
Розглянемо різницю![]()
![]() .
Обчислимо похідну цієї різниці.
.
Обчислимо похідну цієї різниці.
(![]()
![]() )′
=
)′
=![]()
![]() =
=![]()
![]() = 0.
= 0.
Отже, згідно
з теоремою Лагранжа
![]()
![]() =С. Звідси маємо:
=С. Звідси маємо:![]() =
=![]() +С.
+С.
Таким чином,
множина первісних функції
![]() на проміжкуХ, вичерпується
функціями виду
на проміжкуХ, вичерпується
функціями виду![]() +С, де
+С, де![]() одна із первісних
функції
одна із первісних
функції![]() .
.
Означення.Сукупність усіх первісних функції![]() на проміжкуХназивається
невизначеним інтегралом функції
на проміжкуХназивається
невизначеним інтегралом функції![]() на цьому проміжку і позначається
на цьому проміжку і позначається![]() .
.
Невизначений інтеграл інакше називають інтегралом Ньютона Лейбніца.
Якщо
![]() одна з первісних
функції
одна з первісних
функції![]() ,
то за означенням
,
то за означенням
![]() =
=![]() +С.
+С.
Знак
![]() називається
знаком невизначеного інтеграла,
називається
знаком невизначеного інтеграла,![]() підінтегральною
функцією, а
підінтегральною
функцією, а![]() підінтегральним
виразом.
підінтегральним
виразом.
Операцію знаходження невизначеного інтеграла від функції називають інтегруванням цієї функції.
2. Основні властивості невизначеного інтеграла
1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції.
![]() (
(![]() )′=
)′=![]() +
С ′=
+
С ′= ![]() .
.
2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.
![]() d(
d(![]() )=d
)=d![]() =
=
![]() d(x).
d(x).
3. Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної постійної.
![]() =
=![]() .
.
4. Сталий множник можна виносити за знак інтеграла, тобто, якщо k = const 0, то
![]() .
.
Для доведення цієї властивості досить показати, що права чстина рівності є первісною підінтегральної функції:
![]() .
.
5. Невизначений інтеграл від суми (різниці) функцій дорівнює сумі (різниці) невизначених інтегралів від кожної функції, тобто
![]() .
.
Доведення.
![]() .
.
3. Таблиця основних інтегралів
Безпосередньо із означення визначеного інтеграла випливають наступні формули, котрі утворюють таблицю основних інтегралів:
1.![]() ,
,
2.
![]() ,
,
3.
![]() ,
,
4.
![]()
5.
![]() ,
,
6.
![]() ,
,
7.
![]() ,
,
8.
![]() ,
,
9.
![]() ,
,
10.
![]() ,
,
11.
![]() ,
,
12.
![]() ,
,
13.
![]() ,
,
14.
![]()
5. Безпосереднє інтегрування
Обчислення інтегралів за допомогою безпосереднього використання таблиці основних інтегралів та їх властивостей називається безпосереднім інтегруванням.
Приклади.
1.
![]() .
.
2.
![]() .
3.
.
3.![]() .
.
4.
![]() .
.
4. Метод підстановки
В основі методу підстановки (методу заміни змінної) лежить формула диференціювання складеної функції. Якщо F ′( x) = f(x), х(a, b),то для довільної диференційованої на проміжку(, )функції x= (t), де(t) (a, b), якщо t (, )маємо:
(F((t)))′ = F ′( x) ′(t) = f(x) ′(t) = f((t)) ′(t).
Таким чином,
![]() ,
,
тобто
![]()
![]() .
.
Приклади.
1.
Обчислити інтеграл
![]() .
.
Розв’язування.
Покладемо
![]() ,
,
![]()
![]() .
Тоді
.
Тоді
![]() .
.
2.
Обчислити інтеграл
![]() .
.
Розв’язування.
Покладемо
![]() .
Отже,
.
Отже,
![]() .
.
6. Інтегрування частинами
Нехай
функції
![]() і
і![]() визначені й диференційовані на
деякому проміжкуХ. Тоді
визначені й диференційовані на
деякому проміжкуХ. Тоді
![]() .
.
Звідси маємо
![]() .
.
Припустимо,
що інтеграл
![]() існує. Тоді
існує. Тоді
![]() .
.
Оскільки
![]() ,
то
,
то
![]() .
(1)
.
(1)
Довільну
сталу Свключає в себе інтеграл![]() .
.
Формула (1) називається формулою інтегрування частинами.
За цією формулою обчислюються , зокрема інтеграли виду
1)
![]() ,
,
![]() ,
,
![]() ,
,
де
![]()
многочлен n-ного
степеня відноснох,
многочлен n-ного
степеня відноснох,![]() .
Тут слід прийняти
.
Тут слід прийняти
![]() .
.
2)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Тут також
![]()
многочлен n-ного
степеня відноснох.У
цих інтегралах
многочлен n-ного
степеня відноснох.У
цих інтегралах
![]() .
.
Приклади.
![]()
![]() .
.
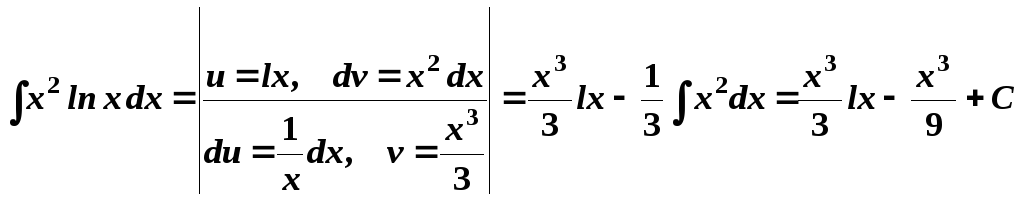 .
.
ЛЕКЦІЯ 24
Подання раціональних дробів у вигляді суми найпростіших дробів.
Інтегрування найпростіших раціональних дробів.
