
- •1. Основні властивості неперервних функцій
- •1. Поняття рівномірної неперервності функції.
- •2. Теорема Кантора про рівномірну неперервність функції.
- •3. Теорема про неперервність оберненої функції.
- •Тема 5. Диференціальне числення функції однієї змінної
- •1. Задачі, що проводять до поняття похідної
- •Після спрощення одержуємо
- •2. Означення похідної
- •3. Механічний та геометричний зміст похідної
- •4. Односторонні похідні
- •5. Нескінченні похідні
- •1. Диференційовність функції
- •2. Похідні елементарних функцій
- •3. Похідна оберненої функції.
- •1. Диференціал функції
- •2. Похідні й диференціали вищих порядків
- •3. Формула Лейбніца для п-ної похідної добутку двох функцій.
- •4. Диференціали вищих порядків.
- •Тема 5. Застосування диференціального числення до дослідження функцій
- •1. Теореми про середнє значення
- •2. Теорема Ферма
- •3. Теорема Ролля
- •4. Теорема Лагранжа
- •5. Теорема Коші
- •1. Розкриття невизначеностей. Правило Лопіталя.
- •2. Застосування правила Лопіталя при розкритті невизначеностей вигляду .
- •1. Формула Тейлора для многочлена. Розглянемо многочлен
- •6.2. Формула Тейлора для довільної функції
- •Звідси одержуємо:
- •1. Ознака монотонності функції
- •3. Необхідні й достатні умови існування екстремуми функції
- •Достатні умови існування екстремуму функції.
- •1. Опуклість та вгнутість кривої. Точки перегину
- •2. Асимптоти графіка функції
- •3. Загальна схема дослідження функцій і побудови їх графіків
- •Тема 7. Інтеграл ньютоналейбніца
- •1. Поняття первісної функції та невизначеного інтеграла
- •2. Основні властивості невизначеного інтеграла
- •3. Таблиця основних інтегралів
- •1. Подання раціональних дробів у вигляді суми найпростіших дробів
- •2. Інтегрування найпростіших раціональних дробів
- •1. Інтегрування ірраціональних функцій
- •Інтегрування деяких тригонометричних функцій
- •Приклади
1. Опуклість та вгнутість кривої. Точки перегину
Нехай функція
![]() визначена на інтервалі
визначена на інтервалі![]() і в кожній точці цього інтервалу має
скінчену похідну. Тоді в кожній точці
і в кожній точці цього інтервалу має
скінчену похідну. Тоді в кожній точці![]() графіка цієї функції можна провести
дотичну, не паралельну осі
графіка цієї функції можна провести
дотичну, не паралельну осі![]() .
Крива, яка є графіком цієї функції,
називається гладкою.
.
Крива, яка є графіком цієї функції,
називається гладкою.
Якщо крива,
яка є графіком функції
![]() ,
розміщена не нижче будь-якої дотичної
на інтервалі
,
розміщена не нижче будь-якої дотичної
на інтервалі![]() ,
то вона називається вгнутою догори або
просто вгнутою на цьому інтервалі. Іноді
її ще називають опуклою вниз (рис. 25).
,
то вона називається вгнутою догори або
просто вгнутою на цьому інтервалі. Іноді
її ще називають опуклою вниз (рис. 25).
Якщо крива,
яка є графіком функції
![]() ,
розміщена не вище будь-якої дотичної
на інтервалі
,
розміщена не вище будь-якої дотичної
на інтервалі![]() ,
то вона називається вгнутою донизу або
просто опуклою на цьому інтервалі. Таку
криву ще називають опуклою вгору (рис.
26).
,
то вона називається вгнутою донизу або
просто опуклою на цьому інтервалі. Таку
криву ще називають опуклою вгору (рис.
26).

 Точка
Точка![]() називається точкою перегину гладкої
кривої
називається точкою перегину гладкої
кривої![]() ,
якщо існує
,
якщо існує![]() -окіл
точки
-окіл
точки![]() такий, що в інтервалах
такий, що в інтервалах![]() і
і![]() крива
крива![]() має опуклість різних напрямків (рис.
27).
має опуклість різних напрямків (рис.
27).

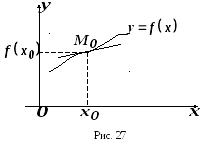
У цьому випадку
графік функції
![]() в інтервалах
в інтервалах![]() і
і![]() лежить по різні боки від дотичної,
проведеної в точці
лежить по різні боки від дотичної,
проведеної в точці![]() .
.
Теорема.Нехай функція![]() визначена на інтервалі
визначена на інтервалі![]() і в кожній точці цього інтервалу має
похідні до другого порядку включно.
Тоді, якщо
і в кожній точці цього інтервалу має
похідні до другого порядку включно.
Тоді, якщо![]() у всіх точках
у всіх точках![]() ,
то графік функції
,
то графік функції![]() на інтервалі
на інтервалі![]() вгнутий (опуклий вниз), якщо ж
вгнутий (опуклий вниз), якщо ж![]() у всіх точках
у всіх точках![]() ,
то графік функції
,
то графік функції![]() на інтервалі
на інтервалі![]() опуклий (опуклий вгору).
опуклий (опуклий вгору).
Доведення.![]() в інтервалах
в інтервалах![]() і
і![]() лежить по різні боки від дотичної,
проведеної в точці
лежить по різні боки від дотичної,
проведеної в точці![]() .
.
Нехай
![]() .
Виберемо точку
.
Виберемо точку![]() і покажемо, що графік функції
і покажемо, що графік функції![]() лежить не нижче дотичної, яка проходить
через точку
лежить не нижче дотичної, яка проходить
через точку![]() .
Щоб відрізняти ординату графіка функції
і ординату дотичної, останню будемо
позначати буквою
.
Щоб відрізняти ординату графіка функції
і ординату дотичної, останню будемо
позначати буквою![]() .
Запишемо рівняння дотичної в точці
.
Запишемо рівняння дотичної в точці![]() :
:
![]() (1)
(1)
Оскільки функція
![]() має похідні до другого порядку включно,
то згідно формули Тейлора (при
має похідні до другого порядку включно,
то згідно формули Тейлора (при![]() )
маємо:
)
маємо:
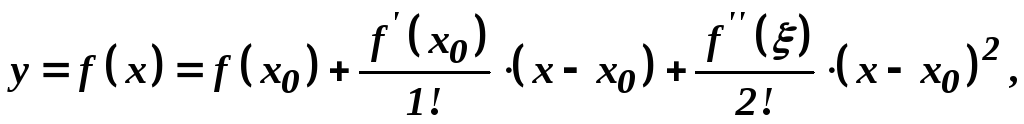 (2)
(2)
де
![]() .
Віднімемо від рівності (2) рівність (1)
.
Віднімемо від рівності (2) рівність (1)
 .
.
Оскільки
![]() ,
то
,
то![]() ,
тобто
,
тобто![]() .
Отже, графік функції
.
Отже, графік функції![]() у будь-якій, відмінній від
у будь-якій, відмінній від![]() ,
точці
,
точці![]() лежить вище дотичної, проведеної до
нього в точці з абсцисою
лежить вище дотичної, проведеної до
нього в точці з абсцисою![]() .
.
Аналогічно
доводиться теорема для випадку
![]() .
.
Установимо
необхідну умову існування точки перегину
графіка функції
![]() .
Нехай функція
.
Нехай функція![]() визначена і має неперервні похідні до
другого порядку включно на інтервалі
визначена і має неперервні похідні до
другого порядку включно на інтервалі![]() .
Тоді. Якщо в кожній точці
.
Тоді. Якщо в кожній точці![]()
![]() ,
то графік функції
,
то графік функції![]() на інтервалі
на інтервалі![]() вгнутий (опуклий вниз). Якщо
вгнутий (опуклий вниз). Якщо![]() ,
,![]() ,то графік опуклий
(опуклий вгору).
,то графік опуклий
(опуклий вгору).
Отже, якщо
на інтервалі
![]()
![]() ,
то графік функції
,
то графік функції![]() точок перегину на цьому інтервалі не
має. Таким чином, точка
точок перегину на цьому інтервалі не
має. Таким чином, точка![]() ,
де
,
де![]() може бути точкою перегину графіка
функції
може бути точкою перегину графіка
функції![]() лише в тому випадку, коли
лише в тому випадку, коли![]() .
.
Отже, умова
![]() є необхідною, для того, щоб точка
є необхідною, для того, щоб точка![]() була точкою перегину графіка функції
була точкою перегину графіка функції![]() .
.

 Покажемо,
що не всяка точка
Покажемо,
що не всяка точка![]() за умови
за умови![]() є точкою перегину. Розглянемо такий
приклад: Нехай
є точкою перегину. Розглянемо такий
приклад: Нехай![]() .
Тоді
.
Тоді![]() при
при![]() .
Але точка
.
Але точка![]() не
є точкою перегину графіка функції
не
є точкою перегину графіка функції![]() (рис.
28).
(рис.
28).
Установимо
достатню умову існування точки перегину
графіка функції
![]() .
Нехай точка
.
Нехай точка![]() така, що
така, що![]() й існує таке
й існує таке![]() ,
що в інтервалах
,
що в інтервалах![]() і
і![]() друга похідна
друга похідна![]() має різні знаки. Тоді точка
має різні знаки. Тоді точка![]() є точкою перегину. Дійсно, за вказаних
умов у інтервалах
є точкою перегину. Дійсно, за вказаних
умов у інтервалах![]() і
і![]() крива
крива![]() має опуклість різних напрямків. Отже,
точка
має опуклість різних напрямків. Отже,
точка![]() є точкою перегину цієї кривої.
є точкою перегину цієї кривої.
Зауваження.Точка![]() є точкою перегину графіка функції
є точкою перегину графіка функції![]() і в тому випадку, коли в точці
і в тому випадку, коли в точці![]() існує дотична до графіка функції
існує дотична до графіка функції![]() ,
друга похідна в самій точці
,
друга похідна в самій точці![]() не існує, але існує в деякому
не існує, але існує в деякому![]() -околі
точки
-околі
точки![]() ,
причому в інтервалах
,
причому в інтервалах![]() і
і![]() має різні знаки.
має різні знаки.
Це установлюється аналогічно попередньому.
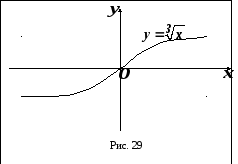 Приклад.Нехай
Приклад.Нехай![]() .
Ця функція в точці
.
Ця функція в точці![]() має нескінченну похідну першого порядку
й дотична до її графіка в точці
має нескінченну похідну першого порядку
й дотична до її графіка в точці![]() співпадає з віссю
співпадає з віссю![]() .
Друга похідна в точці
.
Друга похідна в точці![]() не існує. Графік функції
не існує. Графік функції![]() в точці
в точці![]() має перегин, оскільки справа і зліва
від точки
має перегин, оскільки справа і зліва
від точки![]() друга похідна
друга похідна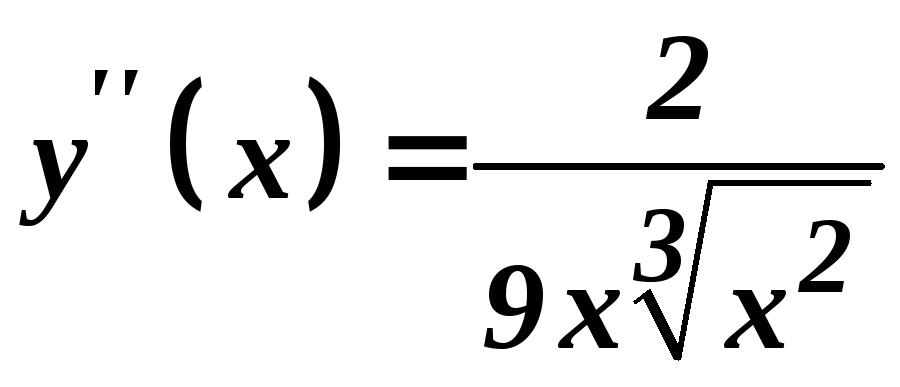 має різні знаки (рис. 29).
має різні знаки (рис. 29).
