
- •1. Основні властивості неперервних функцій
- •1. Поняття рівномірної неперервності функції.
- •2. Теорема Кантора про рівномірну неперервність функції.
- •3. Теорема про неперервність оберненої функції.
- •Тема 5. Диференціальне числення функції однієї змінної
- •1. Задачі, що проводять до поняття похідної
- •Після спрощення одержуємо
- •2. Означення похідної
- •3. Механічний та геометричний зміст похідної
- •4. Односторонні похідні
- •5. Нескінченні похідні
- •1. Диференційовність функції
- •2. Похідні елементарних функцій
- •3. Похідна оберненої функції.
- •1. Диференціал функції
- •2. Похідні й диференціали вищих порядків
- •3. Формула Лейбніца для п-ної похідної добутку двох функцій.
- •4. Диференціали вищих порядків.
- •Тема 5. Застосування диференціального числення до дослідження функцій
- •1. Теореми про середнє значення
- •2. Теорема Ферма
- •3. Теорема Ролля
- •4. Теорема Лагранжа
- •5. Теорема Коші
- •1. Розкриття невизначеностей. Правило Лопіталя.
- •2. Застосування правила Лопіталя при розкритті невизначеностей вигляду .
- •1. Формула Тейлора для многочлена. Розглянемо многочлен
- •6.2. Формула Тейлора для довільної функції
- •Звідси одержуємо:
- •1. Ознака монотонності функції
- •3. Необхідні й достатні умови існування екстремуми функції
- •Достатні умови існування екстремуму функції.
- •1. Опуклість та вгнутість кривої. Точки перегину
- •2. Асимптоти графіка функції
- •3. Загальна схема дослідження функцій і побудови їх графіків
- •Тема 7. Інтеграл ньютоналейбніца
- •1. Поняття первісної функції та невизначеного інтеграла
- •2. Основні властивості невизначеного інтеграла
- •3. Таблиця основних інтегралів
- •1. Подання раціональних дробів у вигляді суми найпростіших дробів
- •2. Інтегрування найпростіших раціональних дробів
- •1. Інтегрування ірраціональних функцій
- •Інтегрування деяких тригонометричних функцій
- •Приклади
2. Асимптоти графіка функції
Пряма
![]() називається асимптотою кривої
називається асимптотою кривої![]() ,
якщо відстань від точки
,
якщо відстань від точки![]() кривої до прямої
кривої до прямої![]() при віддаленні точки
при віддаленні точки![]() у нескінченність прямує до нуля.
у нескінченність прямує до нуля.
Із наведеного означення випливає, що асимптоти можуть існувати лише у тих кривих, які мають як завгодно віддалені точки, тобто у “нескінчених” кривих.
Надалі розрізнятимемо похилі і вертикальні асимптоти. До похилих асимптот належать також і горизонтальні асимптоти.
Теорема. Якщо функція![]() визначена на нескінченості і існують
границі
визначена на нескінченості і існують
границі
 (1)
(1)
то пряма
![]() є похилою асимптотою кривої
є похилою асимптотою кривої![]() при
при![]() .
.
Аналогічно, якщо існують границі
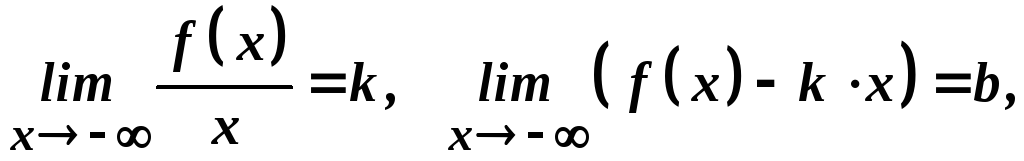 (2)
(2)
то пряма
![]() є похилою асимптотою кривої
є похилою асимптотою кривої![]() при
при![]() .
.
Доведення.Розглянемо випадок![]() .
Оскільки за умовою існують границі (1),
то
.
Оскільки за умовою існують границі (1),
то![]() .
Число
.
Число![]() дорівнює довжині відрізка від точки
дорівнює довжині відрізка від точки![]() прямої
прямої![]() до точки
до точки![]() графіка функції
графіка функції![]() (рис. 30).
(рис. 30).
Рис. 30
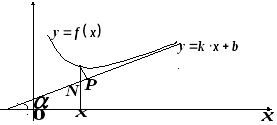
Відстань
![]() від точки
від точки![]() до прямої
до прямої![]() рівна
рівна![]() ,
де
,
де![]() кут, який утворює пряма
кут, який утворює пряма![]() з додатним напрямом вісі
з додатним напрямом вісі![]() (
(![]() ,
оскільки мова йде про похилі асимптоти).
Отже,
,
оскільки мова йде про похилі асимптоти).
Отже,![]() =
=![]() .
Тоді
.
Тоді
![]() .
.
Випадок, коли
![]() доводиться аналогічно.
доводиться аналогічно.
Якщо
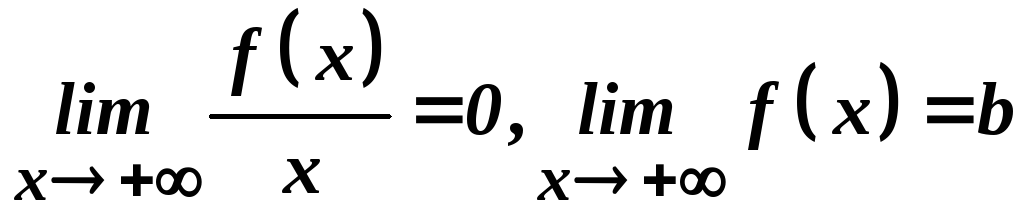 ,
то пряма
,
то пряма![]() є горизонтальною асимптотою графіка
функції
є горизонтальною асимптотою графіка
функції![]() при
при![]() .
Те ж стосується і випадку
.
Те ж стосується і випадку![]() .
.
Зауваження.Якщо не існує границя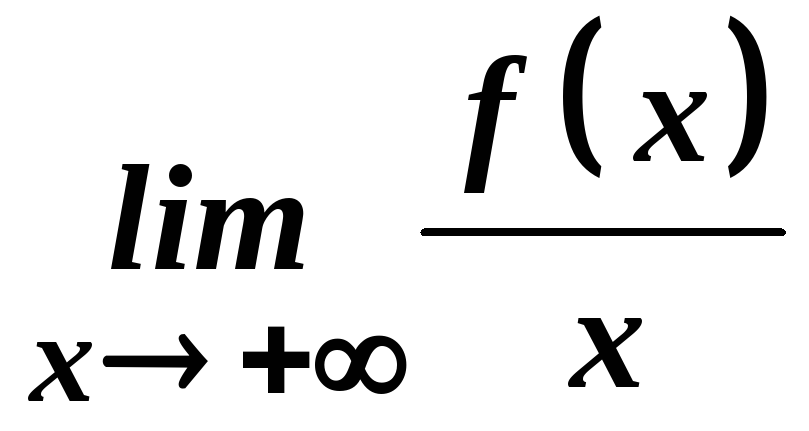 ,
то не існує і границя
,
то не існує і границя![]() .
Отже, у цьому випадку графік функції
.
Отже, у цьому випадку графік функції![]() при
при![]() асимптот не має. Якщо границя
асимптот не має. Якщо границя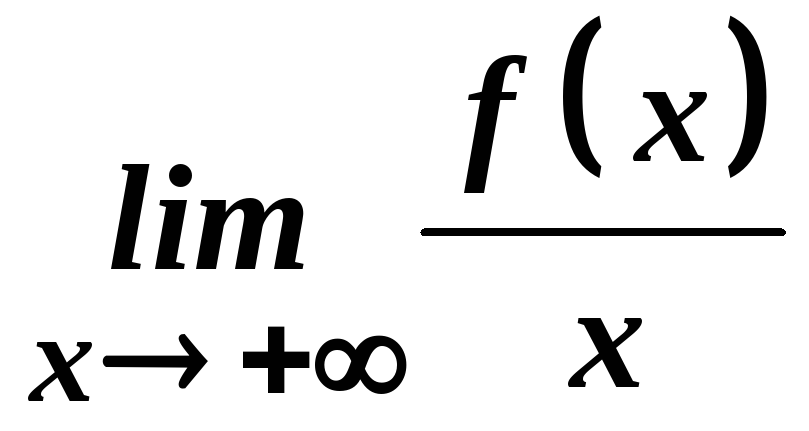 існує і рівна
існує і рівна![]() ,
а границя
,
а границя![]() не існує, то у цьому випадку графік
функції
не існує, то у цьому випадку графік
функції![]() також асимптот не має.
також асимптот не має.
Із означення
асимптоти кривої
![]() випливає, що пряма
випливає, що пряма![]() є вертикальною асимптотою, якщо принаймні
одна з границь
є вертикальною асимптотою, якщо принаймні
одна з границь![]() або
або![]() рівна
рівна![]() або
або![]() .
.
3. Загальна схема дослідження функцій і побудови їх графіків
При дослідженні функцій і побудові їх графіків може бути застосована, наприклад, наступна схема:
Знайти область визначення функції.
Знайти точки розриву та визначити їх тип.
Знайти асимптоти графіка функцій.
Знайти похідну функції і за її допомогою встановити інтервали зростання і спадання функції.
Знайти точки максимуму і мінімуму функції, а також максимальне й мінімальне значення функції.
Знайти другу похідну і за її допомогою визначити інтервали опуклості й точки перегину графіка функції.
Знайти точки перетину графіка функції з осями координат.
Враховуючи одержані результати, побудувати графік функції.
Приклад.Дослідити функцію і побудувати її графік.
і побудувати її графік.
Розв'язування.
Область визначення функції є об'єднання інтервалів
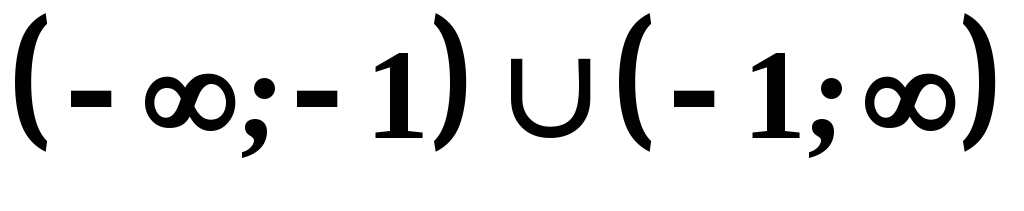 .
.Оскільки функція не визначена в точці
 ,
то з'ясуємо поведінку функції в околі
цієї точки.
,
то з'ясуємо поведінку функції в околі
цієї точки.
 .
.
У точці
![]() функція має розрив другого роду.
функція має розрив другого роду.
Пряма
 є вертикальною асимптотою. Знайдемо
похилі асимптоти.
є вертикальною асимптотою. Знайдемо
похилі асимптоти.

Пряма
![]() є похилою асимптотою.
є похилою асимптотою.
Знайдемо похідну функції, інтервали зростання і спадання
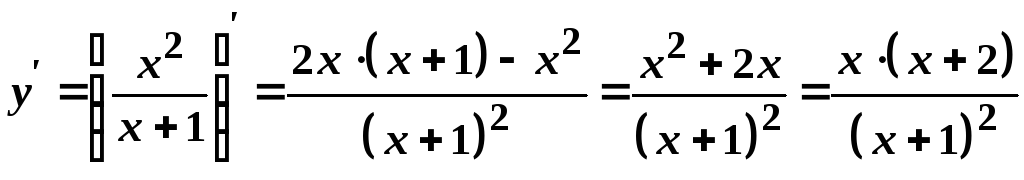 .
.
Похідна функції рівна нулю в точках
![]() і
і![]() .
У точці
.
У точці![]() похідна невизначена. В інтервалі
похідна невизначена. В інтервалі![]() похідна додана, функція зростає; в
інтервалах
похідна додана, функція зростає; в
інтервалах![]() і
і![]() похідна від'ємна, функція спадає; в
інтервалі
похідна від'ємна, функція спадає; в
інтервалі![]() похідна додана, функція зростає.
похідна додана, функція зростає.
Точка
 є точкою максимуму, а точка
є точкою максимуму, а точка є точкою мінімуму функції.
є точкою мінімуму функції.
![]()

З
найдемо другу похідну функції, інтервали опуклості та точки перегину графіка функції.
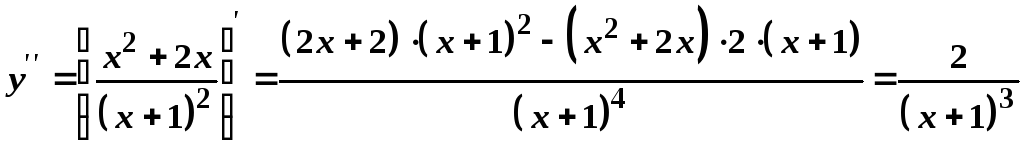 .
.
 Друга
похідна в області визначення функції
нулю не дорівнює. В інтервалі
Друга
похідна в області визначення функції
нулю не дорівнює. В інтервалі![]() друга похідна від'ємна, функція опукла;
в інтервалі
друга похідна від'ємна, функція опукла;
в інтервалі![]() друга похідна додатна, функція вгнута.
Точок перегину графік функції не має.
друга похідна додатна, функція вгнута.
Точок перегину графік функції не має.

Графік функції перетинає координатні вісі в точці
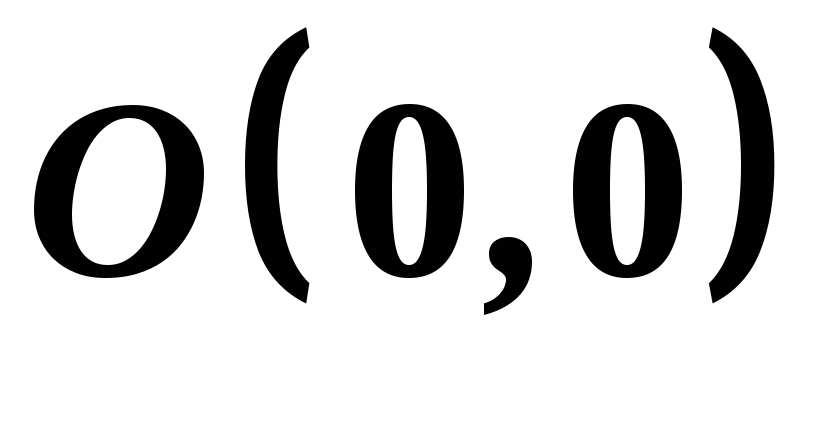 .
.Схема графіка функції зображена на рисунку 31.
Р
 ис.
31
ис.
31




