
- •1. Основні властивості неперервних функцій
- •1. Поняття рівномірної неперервності функції.
- •2. Теорема Кантора про рівномірну неперервність функції.
- •3. Теорема про неперервність оберненої функції.
- •Тема 5. Диференціальне числення функції однієї змінної
- •1. Задачі, що проводять до поняття похідної
- •Після спрощення одержуємо
- •2. Означення похідної
- •3. Механічний та геометричний зміст похідної
- •4. Односторонні похідні
- •5. Нескінченні похідні
- •1. Диференційовність функції
- •2. Похідні елементарних функцій
- •3. Похідна оберненої функції.
- •1. Диференціал функції
- •2. Похідні й диференціали вищих порядків
- •3. Формула Лейбніца для п-ної похідної добутку двох функцій.
- •4. Диференціали вищих порядків.
- •Тема 5. Застосування диференціального числення до дослідження функцій
- •1. Теореми про середнє значення
- •2. Теорема Ферма
- •3. Теорема Ролля
- •4. Теорема Лагранжа
- •5. Теорема Коші
- •1. Розкриття невизначеностей. Правило Лопіталя.
- •2. Застосування правила Лопіталя при розкритті невизначеностей вигляду .
- •1. Формула Тейлора для многочлена. Розглянемо многочлен
- •6.2. Формула Тейлора для довільної функції
- •Звідси одержуємо:
- •1. Ознака монотонності функції
- •3. Необхідні й достатні умови існування екстремуми функції
- •Достатні умови існування екстремуму функції.
- •1. Опуклість та вгнутість кривої. Точки перегину
- •2. Асимптоти графіка функції
- •3. Загальна схема дослідження функцій і побудови їх графіків
- •Тема 7. Інтеграл ньютоналейбніца
- •1. Поняття первісної функції та невизначеного інтеграла
- •2. Основні властивості невизначеного інтеграла
- •3. Таблиця основних інтегралів
- •1. Подання раціональних дробів у вигляді суми найпростіших дробів
- •2. Інтегрування найпростіших раціональних дробів
- •1. Інтегрування ірраціональних функцій
- •Інтегрування деяких тригонометричних функцій
- •Приклади
Звідси одержуємо:
 .
.
Формула (3) називається формулою Тейлора,
а одержаний вираз
![]() залишковим членом
у формі Лагранжа.
залишковим членом
у формі Лагранжа.
Оскільки
![]() ,
то
,
то![]() ,
де
,
де![]() .
Тоді
.
Тоді
 ,
де
,
де![]() .
.
Якщо в формулі
Тейлора покласти
![]() ,
то тоді
,
то тоді
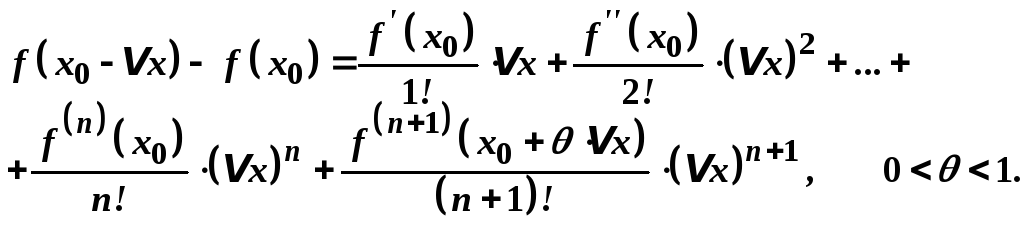
При
![]() маємо формулу Лагранжа
маємо формулу Лагранжа
![]()
Якщо функція
![]() в околі точки
в околі точки![]() обмежена, то залишковий член
обмежена, то залишковий член![]() є нескінченно малою вищого порядку
порівняно з
є нескінченно малою вищого порядку
порівняно з![]() при
при![]() .
Дійсно
.
Дійсно
 .
.
Отже, залишковий член
![]() можна подати у формі
можна подати у формі
![]() при
при![]() ,
,
яка називається формою Пеано.
Якщо в формулі
Тейлора покласти
![]() ,
то одержимо формулу Маклорена
,
то одержимо формулу Маклорена
 .
.
У цій формулі залишковий член у формі Лагранжа має вигляд
 де
де![]() ,
,
а в формі Пеано
![]() .
.
Приклади.Записати формулу Маклорена для функції
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
Розв'язування.
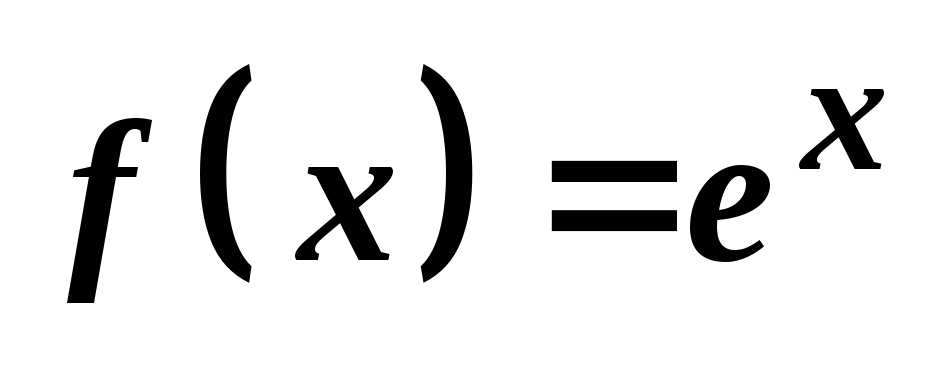 .
Оскільки
.
Оскільки ,
то
,
то .
Отже,
.
Отже,
 .
.
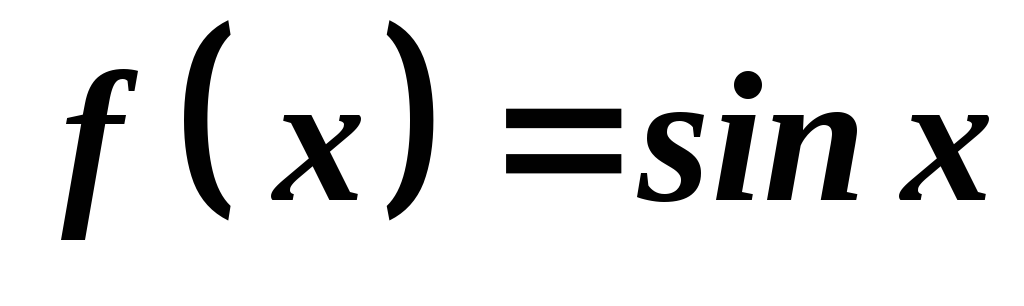 .
Так як
.
Так як ,
то
,
то

Звідси маємо
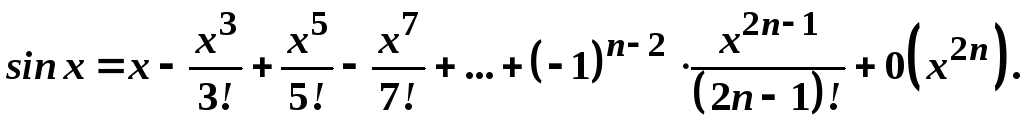
 .
.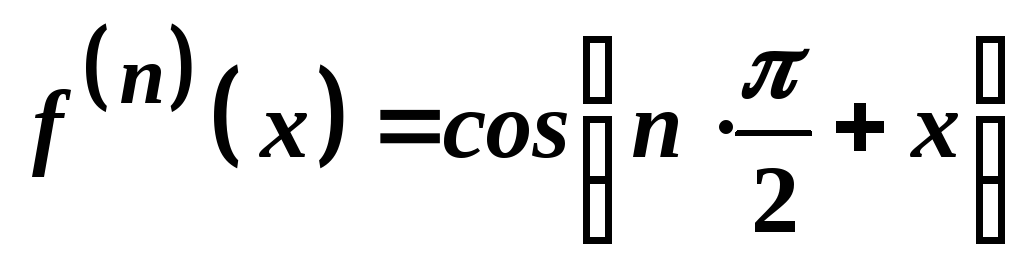 ;
;
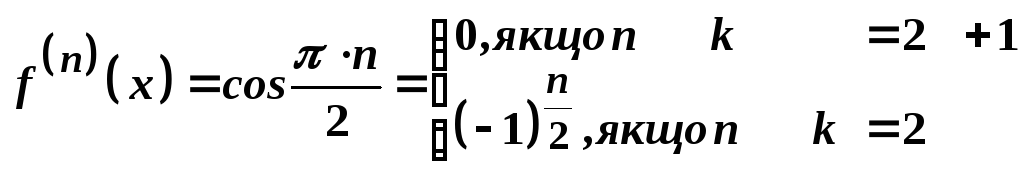 ;
;
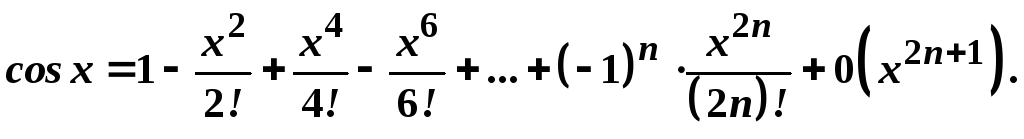
ЛЕКЦІЯ 21
Ознака монотонності функції.
Екстремальні точки.
Необхідні й достатні умови існування екстремуми функції.
4. Знаходження найбільшого й найменшого значення функції на відрізку.
1. Ознака монотонності функції
Теорема .Якщо функція![]() диференційована на інтервалі
диференційована на інтервалі![]() і
і![]() на
на![]() ,
то функція
,
то функція![]() зростає (спадає).
зростає (спадає).
Доведення.Нехай для визначеності![]() .
Візьмемо в інтервалі
.
Візьмемо в інтервалі![]() дві довільні точки
дві довільні точки![]() такі, що
такі, що![]() .
На відрізку
.
На відрізку![]() функція
функція![]() задовольняє умовам теореми Лагранжа.
Отже, існує точка
задовольняє умовам теореми Лагранжа.
Отже, існує точка![]() така,
що
така,
що
 .
.
Звідси випливає, що за умов
![]() і
і![]() маємо:
маємо:![]() ,
тобто
,
тобто![]() .
.
Для випадку
![]() доведення аналогічне.
доведення аналогічне.
2. Екстремальні точки
Точка
![]() називається точкою локального максимуму
(мінімуму) функції
називається точкою локального максимуму
(мінімуму) функції![]() ,
якщо існує
,
якщо існує![]() -
окіл
-
окіл![]() точки
точки![]() такий, що
такий, що![]() для будь-якої відмінної від
для будь-якої відмінної від![]() точки
точки![]() .
При цьому саме значення
.
При цьому саме значення![]() називається локальним максимумом
(мінімумом) функції
називається локальним максимумом
(мінімумом) функції![]() .
.
Точки максимуму
і мінімуму функції
![]() називаються точками екстремуму або
екстремальними точками функції
називаються точками екстремуму або
екстремальними точками функції![]() .
.
3. Необхідні й достатні умови існування екстремуми функції
Необхідна умова існування локального
екстремуму функції.Якщо в точці![]() функція
функція![]() має екстремум, то існує окіл
має екстремум, то існує окіл![]() точки
точки![]() ,
в якому значення
,
в якому значення![]() є найбільшим або найменшим. Отже, якщо
в точці
є найбільшим або найменшим. Отже, якщо
в точці![]() функція
функція![]() диференційована, то згідно теореми
Ферма
диференційована, то згідно теореми
Ферма![]() .
.
Зазначимо,
що коли функція
![]() диференційована в точці
диференційована в точці![]() і
і![]() ,
то або
,
то або![]() ,
тобто функція зростає, або
,
тобто функція зростає, або![]() і функція спадає. Звідси випливає, що
функція
і функція спадає. Звідси випливає, що
функція![]() може мати екстремум лише в тих точках,
у яких її похідна
може мати екстремум лише в тих точках,
у яких її похідна![]() рівна нулю, або не існує.
рівна нулю, або не існує.
Точки, в яких
похідна функції
![]() рівна нулю, називаються стаціонарними.
Стаціонарні точки й точки, в яких функція
рівна нулю, називаються стаціонарними.
Стаціонарні точки й точки, в яких функція![]() визначена, але її похідна
визначена, але її похідна![]() не існує називаються критичними.
не існує називаються критичними.
Отже, для
того, щоб функція
![]() мала в точці
мала в точці![]() екстремуму, необхідно, щоб ця точка була
критичною.
екстремуму, необхідно, щоб ця точка була
критичною.
Достатні умови існування екстремуму функції.
Теорема.Нехай![]() критична точка
функції
критична точка
функції![]() ,
,![]() неперервна в точці
неперервна в точці![]() і має похідну
і має похідну![]() в усіх точках околу
в усіх точках околу![]() за виключенням, можливо самої точки
за виключенням, можливо самої точки![]() .
Тоді
.
Тоді
якщо
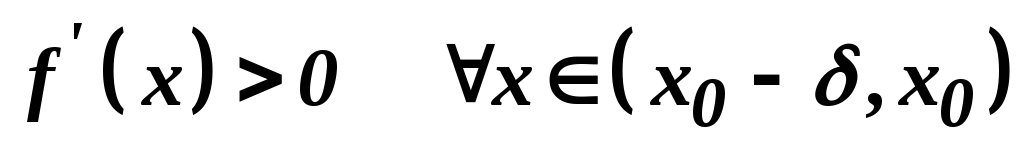 і
і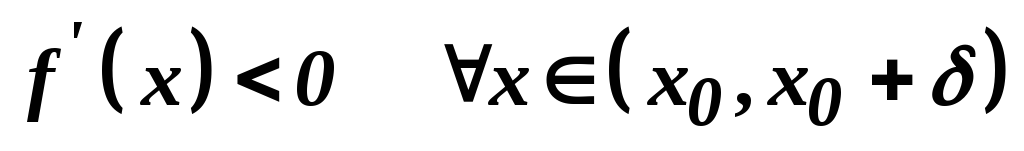 ,
то точка
,
то точка є точкою максимуму функції
є точкою максимуму функції .
.якщо
 і
і ,
то точка
,
то точка є точкою мінімуму функції
є точкою мінімуму функції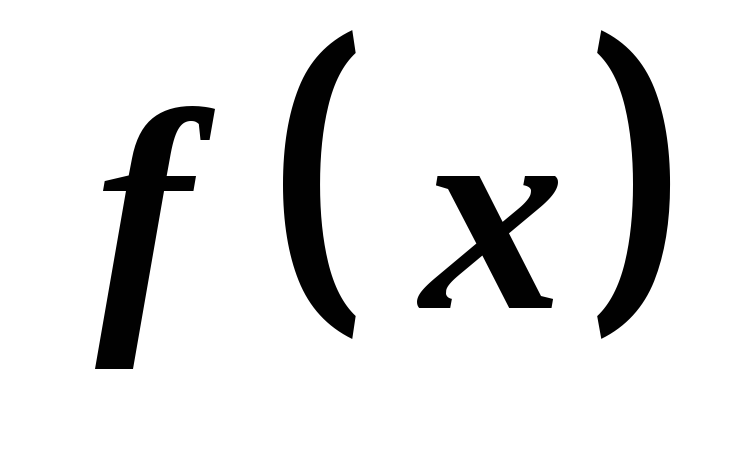 .
.Якщо
 в околі
в околі має один і той же знак, то
має один і той же знак, то не є точкою екстремуму функції
не є точкою екстремуму функції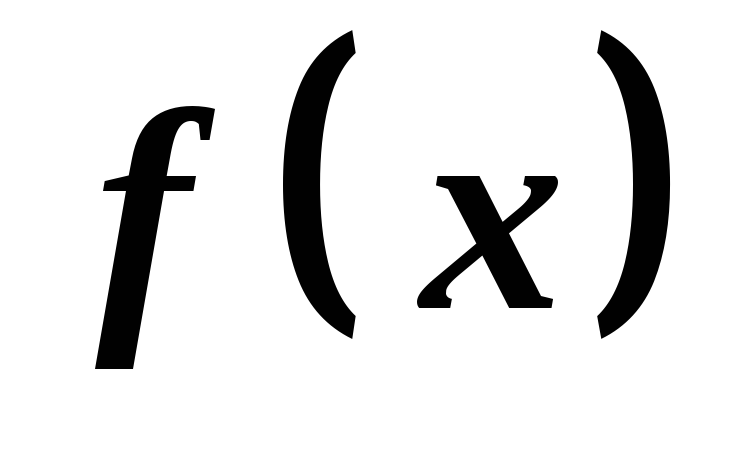 .
.
Доведення.1). Нехай![]() і
і![]() .
Звідси за ознаками монотонності функції
маємо: якщо
.
Звідси за ознаками монотонності функції
маємо: якщо![]() і
і![]() .
Отже, для будь-якого
.
Отже, для будь-якого![]() із околу
із околу![]() виконується нерівність
виконується нерівність![]() ,
тобто точка
,
тобто точка![]() є точкою максимуму функції
є точкою максимуму функції![]() .
.
Доведення пунктів 2), 3) аналогічні.
Із сказаного
випливає правило дослідження
функції на екстремум. Щоб дослідити
функцію![]() на екстремум треба:
на екстремум треба:
Знайти область визначення функції.
Знайти
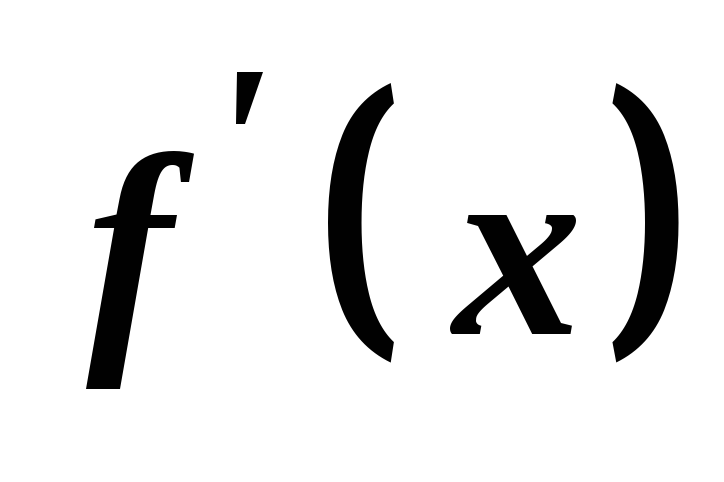 першу похідну
функції
першу похідну
функції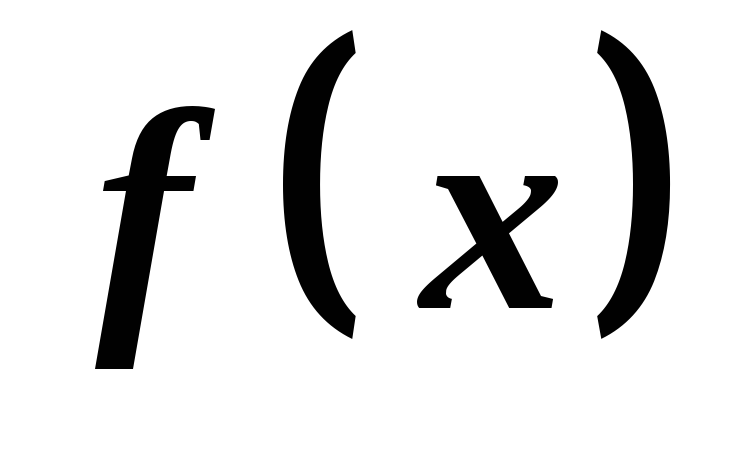 .
.Розв’язати рівняння
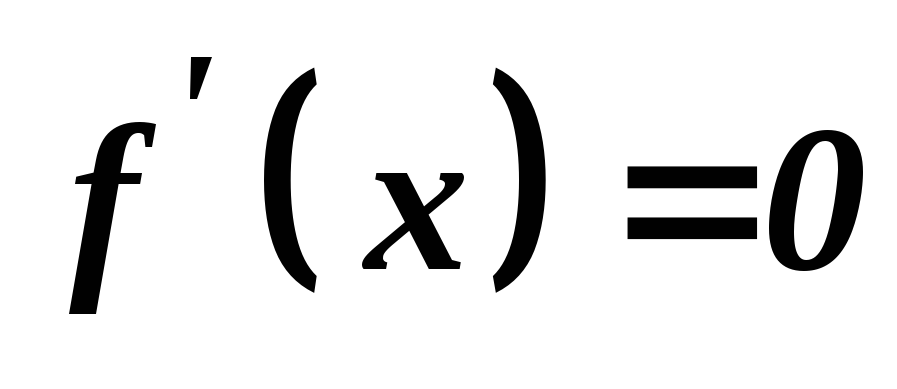 та визначити ті значення
та визначити ті значення ,
при яких
,
при яких або
або не існує. Нехай після виконання цих дій
одержано точки
не існує. Нехай після виконання цих дій
одержано точки ,
які знаходяться в інтервалі
,
які знаходяться в інтервалі області визначення функції
області визначення функції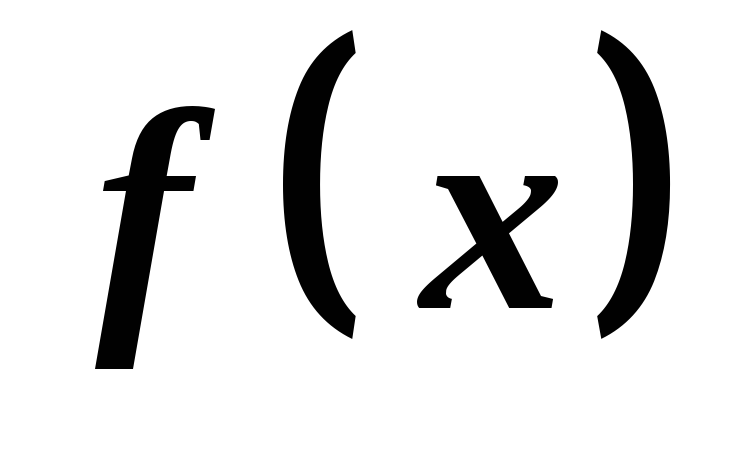 .
.У кожному з інтервалів
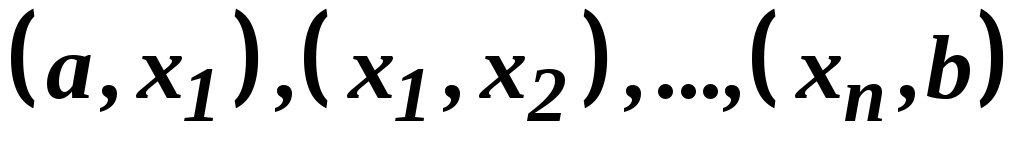 взяти довільну точку і визначити в ній
знак першої похідної. Який знак матиме
похідна у вибраній точці, такий же знак
вона матиме й у відповідному інтервалі.
взяти довільну точку і визначити в ній
знак першої похідної. Який знак матиме
похідна у вибраній точці, такий же знак
вона матиме й у відповідному інтервалі.Розглянути знак
 у сусідніх інтервалах, переходячи
послідовно зліва направо від першого
інтервалу до останнього. Якщо при цьому
знаки
у сусідніх інтервалах, переходячи
послідовно зліва направо від першого
інтервалу до останнього. Якщо при цьому
знаки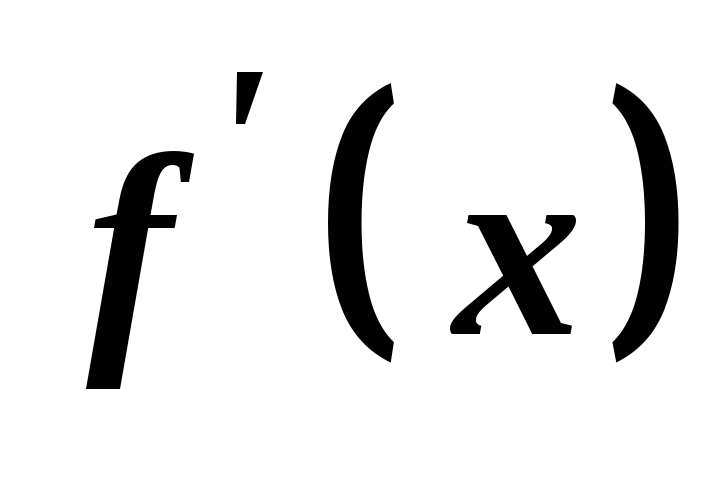 у двох сусідніх інтервалах різні. То в
критичній точці є екстремум: максимум,
якщо знак змінюється з “+” на “-“,
мінімум, якщо знак змінюється з “-“ на
“+”. Якщо ж у двох сусідніх інтервалах
знак першої похідної не змінюється. То
екстремуму у відповідній критичній
точці немає.
у двох сусідніх інтервалах різні. То в
критичній точці є екстремум: максимум,
якщо знак змінюється з “+” на “-“,
мінімум, якщо знак змінюється з “-“ на
“+”. Якщо ж у двох сусідніх інтервалах
знак першої похідної не змінюється. То
екстремуму у відповідній критичній
точці немає.
Приклад.Дослідити на екстремум функцію
![]() .
.
Розв’язування.
1. Функція визначена в інтервалі
![]() .
.
2.
![]() .
.
3. Розв’язками рівняння
![]() є
є![]() .
.
4. В інтервалі
![]() ,
функція спадає; в інтервалі
,
функція спадає; в інтервалі![]() ,
функція зростає; інтервалі
,
функція зростає; інтервалі![]() ,
функція спадає; в інтервалі
,
функція спадає; в інтервалі![]() ,
функція зростає.
,
функція зростає.
5. Точки
![]() є точками мінімуму, а точка
є точками мінімуму, а точка![]() є точкою максимуму даної функції.
є точкою максимуму даної функції.
6.
![]() .
.
Для знаходження екстремумів функції
![]() можна застосовувати другу похідну
можна застосовувати другу похідну![]() .
Це випливає із наступної теореми.
.
Це випливає із наступної теореми.
Теорема . Нехай![]() стаціонарна точка
функції
стаціонарна точка
функції![]() і в цій точці існує похідна другого
порядку
і в цій точці існує похідна другого
порядку![]() .
Тоді, якщо
.
Тоді, якщо![]() ,
то точка
,
то точка![]() є точкою мінімуму функції
є точкою мінімуму функції![]() ,
а якщо
,
а якщо![]() ,
то – максимуму.
,
то – максимуму.
Доведення.Згідно з умовою теореми![]() .
Нехай
.
Нехай![]() .
Тоді похідна
.
Тоді похідна![]() в точці
в точці![]() є зростаючою функцією, а тому існує окіл
є зростаючою функцією, а тому існує окіл![]() точки
точки![]() такий, що
такий, що![]() і
і![]() .
Оскільки
.
Оскільки![]() ,
то
,
то![]() і
і![]() ,
тобто при переході через точку
,
тобто при переході через точку![]() похідна
похідна![]() змінює свій знак з ““
на “+”. Отже, точка
змінює свій знак з ““
на “+”. Отже, точка![]() є точкою мінімуму функції
є точкою мінімуму функції![]() .
.
Випадок, коли
![]() досліджується аналогічно.
досліджується аналогічно.
Скориставшись формулою Тейлора, можна довести наступну теорему.
Теорема.Якщо в стаціонарній точці![]() функції
функції![]() перша відмінна від нуля похідна
перша відмінна від нуля похідна![]() є похідною парного порядку, то точка
є похідною парного порядку, то точка![]() є точкою екстремуму функції
є точкою екстремуму функції![]() :
точкою мінімуму, якщо
:
точкою мінімуму, якщо![]() і точкою максимуму, якщо
і точкою максимуму, якщо![]() .
Якщо ж перша відмінна від нуля похідна
.
Якщо ж перша відмінна від нуля похідна![]() є похідною непарного порядку, то точка
є похідною непарного порядку, то точка![]() не є точкою екстремуму функції
не є точкою екстремуму функції![]() .
.
4. Знаходження найбільшого й найменшого значення функції на відрізку
Для знаходження найбільшого й найменшого
значення функції
![]() ,
неперервної на відрізку
,
неперервної на відрізку![]() ,
потрібно знайти всі її локальні екстремуми
на цьому відрізку та її значення на
кінцях відрізка, тобто
,
потрібно знайти всі її локальні екстремуми
на цьому відрізку та її значення на
кінцях відрізка, тобто![]() .
Потім з одержаних значень вибрати
найменше й найбільше.
.
Потім з одержаних значень вибрати
найменше й найбільше.
ЛЕКЦІЯ 22
Опуклість та вгнутість кривої. Точки перегину.
Асимптоти графіка функції.
Загальна схема дослідження функцій і побудови їх графіків.
