39. Інтегрування деяких тригонометричних функцій

Розглянемо деякі типи інтегралів від тригонометричних функцій, які обчислюються в скінченному вигляді. До них належать інтеграли від раціональних функцій відносно функцій ,,,,,. Оскільки функції,,тараціонально визначаються черезта, то мова піде про інтеграли виду

, (33)

де – раціональна функція відта.

Інтеграли такого виду можна звести до інтегралів від раціональної функції за допомогою так званої універсальної тригонометричної підстановки

.

Справді,

;

.

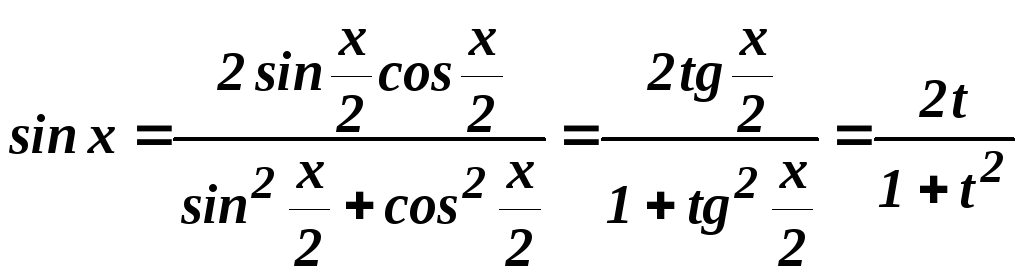Крім того,

.

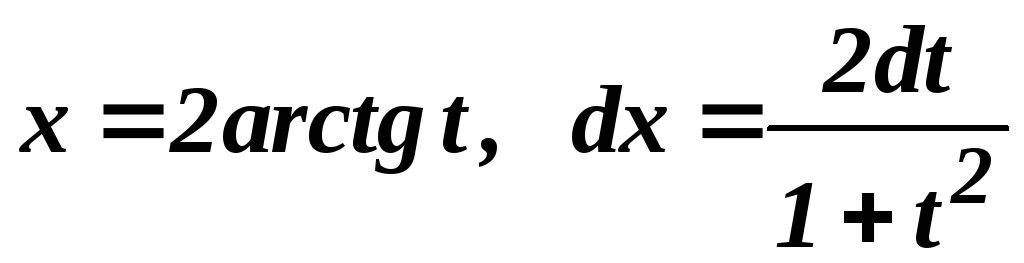Інтеграл (33) після заміни змінної (34) набуває вигляду

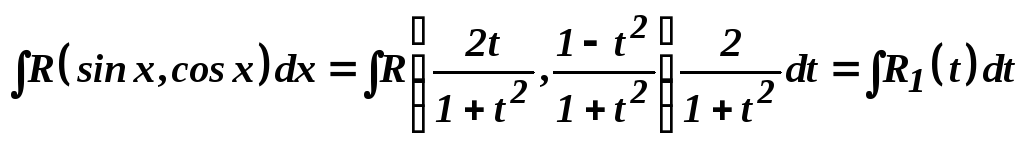, де

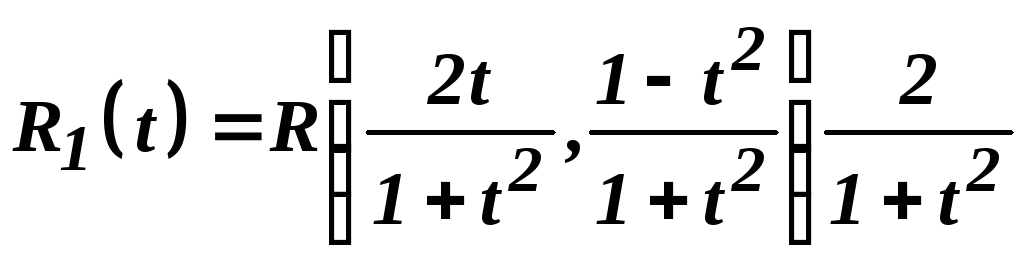– раціональна функція від змінної.

Таким чином, інтеграл виду (33) завдяки підстановці (34) завжди можна обчислити в скінченому вигляді. Однак застосування підстановки (34) не завжди доцільне. В окремих випадках можна використати інші, простіші методи. Це стосується, зокрема, інтегралів виду

; (35)

, (36)

де – ціле число;та– раціональні функції від своїх аргументів.

Для обчислення інтеграла (35) застосуємо підстановку

. (37)

Матимемо

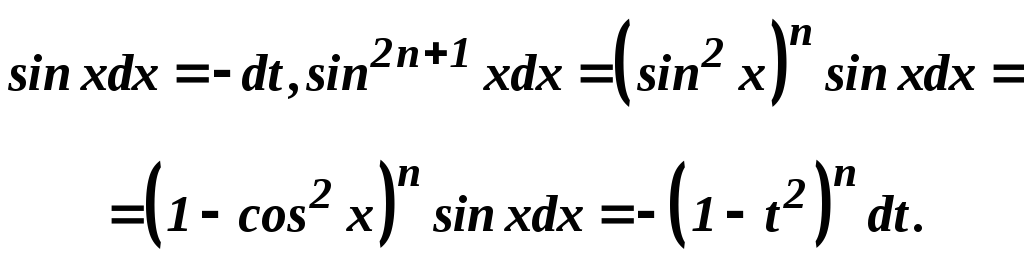
Отже,

,

де – раціональна функція від.

Аналогічно, якщо скористатися підстановкою

,

то інтеграл (36) набуває вигляду

,

де – раціональна функція від.

При обчисленні інтегралів від тригонометричних функцій часто доводиться користуватися відомими формулами тригонометрії.

Розглянемо інтеграли

. (39)

Для знаходження цих інтегралів застосовують такі формули:

;

;

.

Якщо , то перший з інтегралів (39) обчислюють так:

Аналогічно обчислюють і два інші інтеграли.

При інтеграли (39) обчислюють так:

; (40)

; (41)

. (42)

Якщо , то, використовуючи непарність функціїта парність функції, знаходження інтегралів (39) зводиться до випадку.

Зауважимо, що метод обчислення інтегралів (40) і (42) використовується і для інтегралів виду та.

Приклади

Знайти інтеграли: 1) ; 2); 3); 4).

Розв‘язання

1. 

Застосуємо підстановку .

Тоді

,,.

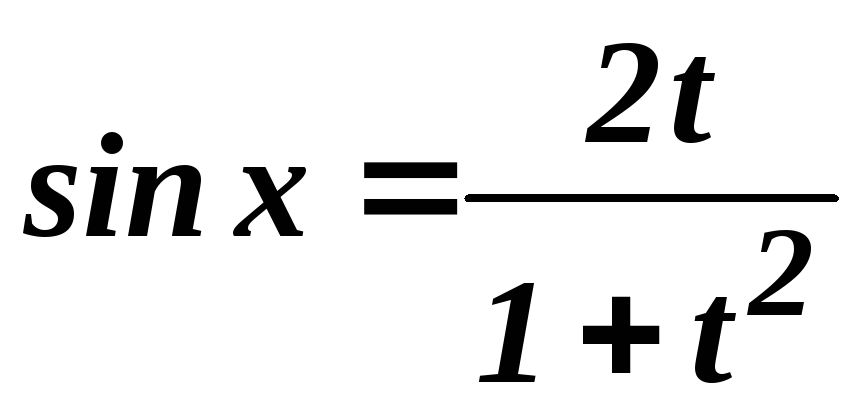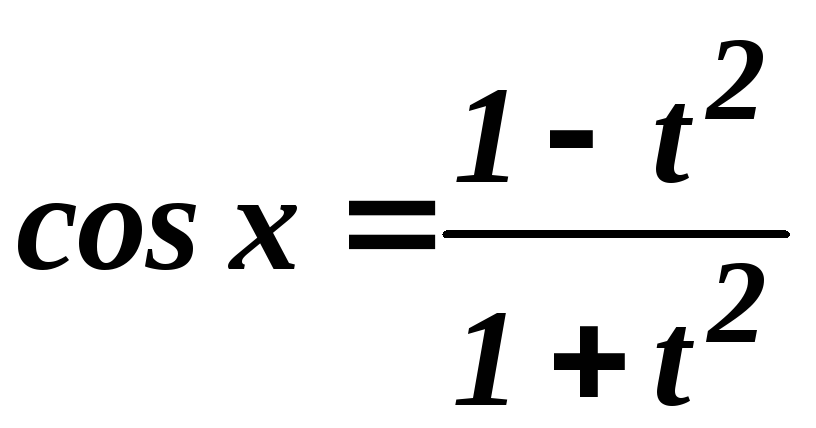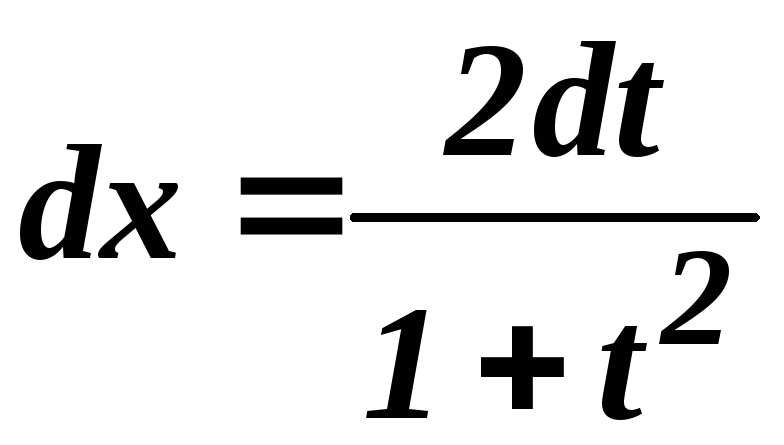Маємо

2. 

3. 

4. 

69