Тема 2. Загальні принципи побудови систем передачі даних

В телекомунікаційних системах загальноприйнятим є перетворення довільного інформаційного сигналу в електричне коливання напруги або в певний тип електромагнітної хвилі. При передачі повідомлення від джерела до отримувача необхідно створити канал зв’язку. Він повинен забезпечити послідовне перетворення інформаційного сигналу а(t) в сигнал повідомлення, транслювати сигнал повідомлення до певного виду, зручного для передачі через певний вид середовища, виділити на приймаючій стороні сигнал і відтворити з нього необхідну інформацію.

Канал зв’язку, що включає передаючу і приймальну частини називають щесистемою передачі даних або телекомунікаційною системою. Назва “телекомунікаційна система” пішла від передачі різного типу інформації: акустичних, високочастотних повідомлень, телевізійного зображення і т. д.

В будь-якому каналі зв’язку діють електромагнітні завади, які призводять до спотворення сигналів. В результаті іможуть відрізнятися від їх аналогів на передаючій стороні.

Для перевірки достовірності використовують певні засоби контролю: таблиці кольоровості та контрастності для телевізійних сигналів, розрахунок кількості біт і т. д. Якість передачі даних визначається швидкістю, а відповідно і типом каналу зв’язку. Для передачі інформації використовують електричні і електромагнітні коливання, в діапазоні віддоГц. Діапазон віддоназивають діапазоном провідного мовлення;використовується для так званого кабельного зв’язку;- діапазон радіозв’язку;- радіорелейний зв’язок;- системи супутникового зв’язку;- системи оптичного зв’язку.

Тема 3. Сигнали і спектри §3.1 Поняття про часове і спектральне представлення сигналів

Всі відомі сигнали можна поділити на 2 класи: періодичні і неперіодичні (випадкові). Особливістю інформаційних сигналів є випадковість їх появи.

Як показано в теорії рядів Фур’є, будь-який хаотичний сигнал можна представити певним набором строго періодичних, гармонічних коливань фіксованих частот. Такий набір коливань називається спектром. Його відображають у вигляді лінійної шкали частот, де кожній гармонічній складовій відповідає лінія, довжина якої пропорційна амплітуді коливань певної частоти.

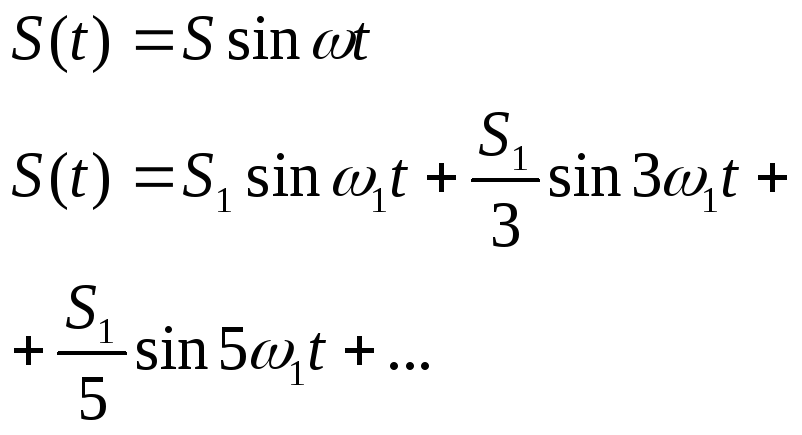
Аналогічно для трикутної форми сигналу:

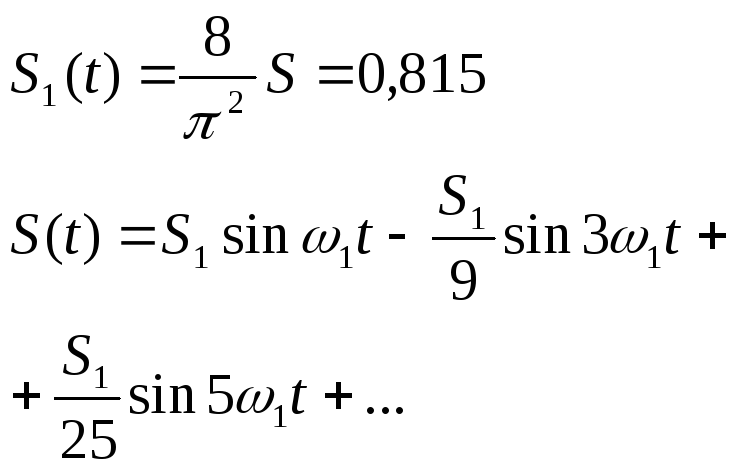
Аналогічно можна представити косинусоїдний сигнал:

Можна записати загальний ряд, який буде містити як синусоїдальні так і косинусоїдальні сигнали.

Узагальнений ряд приймає вигляд:

(1)

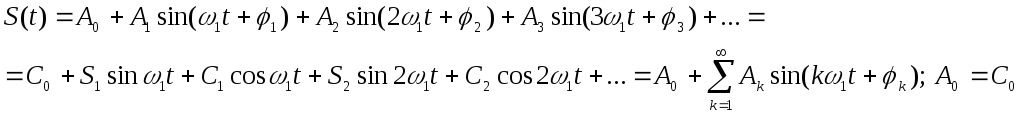
Формула (1) – ряд Фур’є, який описується в узагальненому вигляді.

Розподіл амплітуд А_к та фаз φ_к за частотою називають відповідно амплітудним та фазовим спектром сигналу.

§3.2 Спектральні характеристики періодичних сигналів

Спектр періодичного сигналу є дискретним, оскільки складається з окремих ліній на шкалі частот. Частота першої гармоніки визначається періодом сигналу ω=2п/Т.

Згідно принципу суперпозиції полів та закону збереження енергії, кожна складова спектру переносить певну частину енергії, що передається сигналом вцілому. Оскільки ряд Фур’є є безмежним і він застосовується для представлення прямокутних імпульсів, то зрозуміло, що з підвищенням частоти, енергія кожної гармоніки повинна зменшуватись. Якщо можна представити сигнал з певною точністю (у %) відносно амплітудних значень гармонік або значень енергії сигналу, то такий ряд можна обмежити певним набором частот. Смугу частотного діапазону, в якому набір гармонік із заданим степенем точності відтворює реальний сигнал називають шириною спектру сигналу. Існує загальна закономірність: чим менша тривалість фронту сигналу або менша тривалість імпульсного сигналу, тим більш широкий спектр гармонік необхідно використати для точного відтворення цього сигналу. Для характеристики спектру вводять поняття «спектральної густини сигналу», що характеризує розподіл енергії або потужності в певному діапазоні частот.

В загальному випадку для періодичного сигналу використовують його нормоване представлення x(t) та одиничне навантаження R_н=1Ом.

Тоді енергія і потужність визначаються відповідними інтегралами.

Використовуючи теорему Парсеваля можна виразити сигнал в частотному діапазоні через відповідну залежність в певному часовому інтервалі (-∞;∞).

- Фур’є образ періодичного сигналу;

- спектральна густина енергії (ESD).

Геометричний зміст її відповідає прямокутнику на частотному спектрі сигналу (розмірність Дж/Гц). Оскільки - парна функція, то можна записати:

Для періодичного сигналу використовують теорему Парсеваля, аналогічно можна представити спектральний розподіл потужності інформаційного сигналу (PSD).

- коефіцієнти комплексного ряду Фур’є.

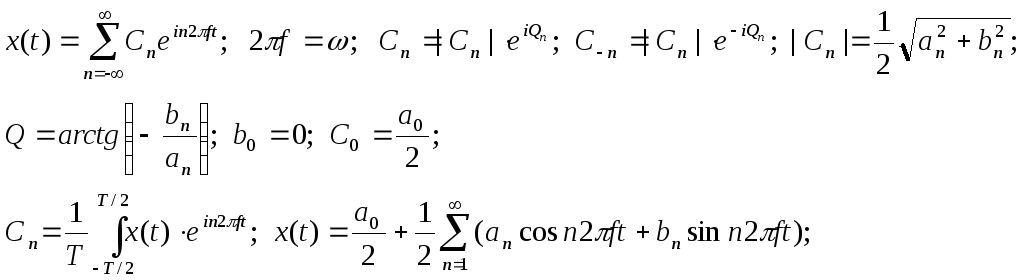
Оскільки спектральна густина потужності, як і енергії є дискретною функцією, то її можна представити, використовуючи одиничну δ-функцію:

- властивість δ-функції.

Середнє нормоване значення потужності дійсного сигналу:

- для періодичного сигналу;

- для неперіодичного сигналу.

Автокореляцією називається процес узгодження сигналу зі своєю копією (відбитком), зсуненим на певний час τ.

Спектральні залежності густини енергії та густини потужності є автокореляційними функціями, що кратно повторюються з періодом 2πп.

Властивості автокореляційної функції:

1. R_x(τ) = R_x(-τ) – функція симетрична відносно нуля;

2. R_x(τ) ≤ R_x(0);

3. Автокореляційна функція та густина енергетичного спектру є фур’є образами одне іншого. .

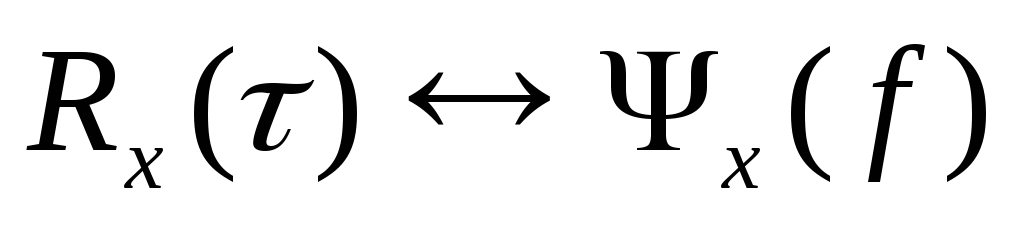З останньої властивості слідує, що

Такий сигнал називається енергетичним сигналом. Він може бути потужнісним сигналом. Для цього сигналу автокореляційна функція записується як: