4.1.1. Спектри сигналів ам-коливань

В АМ-коливаннях (4.1)

Накладання інформаційного модулюючого повідомлення приводить до зміни амплітуди з часом:

(4.2)

Якщо (4.1) переписати з урахуванням (4.2), тоді несучі коливання будуть змінюються з часом:

(4.3)

Тут введено позначення:

U_AM – глибина амплітудної модуляції. При U_AM=0 отримується не модульоване несуче коливання. Якщо врахувати, що:

,

то (4.3) можна записати так:

(4.4)

Таким чином АМ-коливання, крім несучої частоти мають дві бічні гармоніки (ω+Ω) та (ω-Ω).

Якщо коливання інформаційного сигналу містять гармоніки зі спектру Ω_min – Ω_max, то амплітудно-модульоване коливання буде містити дві бічні смуги з відповідною шириною спектру.

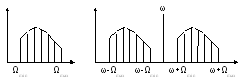
Основна потужність сигналу переноситься несучим коливанням ω.

4.1.2. Спектри сигналів з кутовою модуляцією

При кутовій модуляції (4.5)

- девіація частоти, відхилення частоти від нормованого значення.

(4.6)

Тут введено позначення - індекс фазової модуляції.

Загальний вигляд несучих коливань:

(4.7)

(4.8)

Враховуючи (4.5) і (4.8) при ψ=0 можемо записати:

Якщо позначити , то:

(4.9)

Аналогічно, враховуючи (4.6) і (4.7) для фазо-модульованого коливання:

(4.10)

Як видно із (4.9) та (4.10) розрізнити ФМ та ЧМ-модуляцію дуже складно. Використовуючи відоме з теорії функцій Бесселя співвідношення для комплексних функцій, можна записати:

, (4.11)

де J_n(m) – функція Бесселя І роду, n-ного порядку, яка визначається:

(4.11а)

Враховуючи, що (4.9) та (4.10) можна описати дійсною частиною комплексного числа, тобто представити у вигляді:

(4.12)

Можна знайти спектр ЧМ та ФМ-коливань, якщо перейти в (4.12) до тригонометричної форми запису, тоді другу експоненту можна записати у вигляді суми ряду (4.11).

(4.13)

Враховуючи те, що дійсна частина є сумою дійсних частин доданків суми ряду, а також співвідношення для коефіцієнтів функції Бесселя (4.11а) в кінцевому вигляді (4.13) буде мати вигляд:

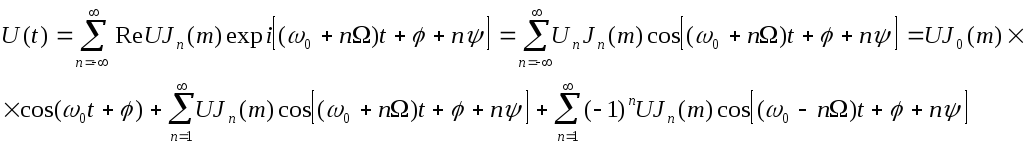(4.14)

О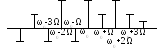держаний спектр складається з безмежного числа бічних гармонік ω₀±nΩ, однак для непарних верхніх і нижніх складових фазові коливання знаходяться в протифазі.

4.1.3. Особливості імпульсної модуляції. Спектр сигналу амплітудно-імпульсних модульованих коливань

При імпульсній модуляції в якості несучих коливань використовуються низькочастотні імпульсні сигнали прямокутної форми, які називаються відео імпульсними. Заповнення їх здійснюється високочастотними сигналами, що називаються радіоімпульсами. Взагалі від вибору параметрів відео імпульсу для кодування інформаційного сигналу, а саме амплітуди, тривалості імпульсу, частоти чи фази розрізняють амплітудно-імпульсну, широтно-імпульсну, частотно-імпульсну чи фазо-імпульсну модуляцію. Теоретичною основою є теорема Котельникова. Формується вона таким чином.

Якщо неперервна функція від часу х(t) має спектр обмежений смугою частот 0-F, то вона повністю визначається послідовністю своїх миттєвих значень, взятих у момент часу, які відраховані через інтервали Δt=1/2F.

Якщо функція може бути представлена набором гармонічних складових з найнижчою частотою F, то частота дискретизації, тобто вибірок миттєвих значень, повинна бути не менше, ніж у два рази вищою за частоту найвищої гармоніки.

На практиці частоту дискретизації вибирають більш високою, оскільки будь-який інформаційний сигнал є обмеженим в часі, а відповідно спектр його може бути представлений у вигляді безмежного ряду. Найпростіший випадок імпульсної модуляції – це АІМ-коливання. Послідовність прямокутних імпульсів, що задає несучі коливання, описується функцією:

(4.15)

Модулювання такої послідовності імпульсів з допомогою , визначається співвідношенням:

(4.16)

Якщо послідовність імпульсів (4.15) представити у вигляді ряду Фур’є і підставити у (4.16), то одержимо функцію АІМ-коливань, що описується співвідношенням:

(4.17)

Підставляємо (4.17) у (4.16):

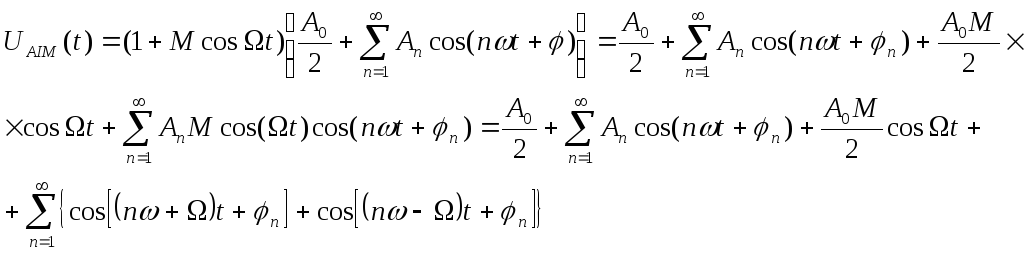(4.18)

Особливістю для одержаного спектру для виразу (4.18) є те, що біля кожної складової nω є додаткові дві лінії з частотами nω­Ω та nω+Ω, амплітуди цих складових визначаються половинним добутком амплітуди несучого коливання та модульованого сигналу.

Для зменшення похибки дискретизації вхідні коливання при використанні АІМ тактову частоту імпульсів вибирають з умови ω>(2÷5)Ω_max, .