§7.2 Векторне представлення сигналів і шумів. Ортогональні сигнали. Нормоване значення енергії цифрового сигналу

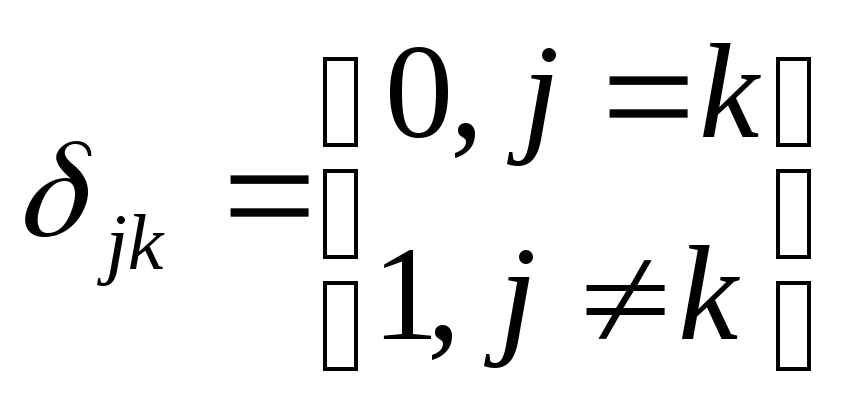Як високочастотні, так і шумові сигнали можна представити з допомогою певного векторного базису. N- мірним ортогональним простором називається набір N лінійно незалежних функцій {ψ_j(t)}, які є базисними векторами цього простору. Довільну функцію можна виразити з допомогою лінійних комбінацій інших функцій, що задовільняють умові:

(І) (ІІ)

При всіхk_j, які не дорівнюють нулю, базис утвореної функції ψ_j називають ортогональним. Якщо k приймає в усіх випадках значення 1, то такий базис називають ортонормованим. Це означає, що кожна з базисних функцій має бути лінійно незалежною від інших. Нормована енергія, яка виражена через квадрат амплітуди струму або напруги, що нормовані на опір 1Ом, може бути записана у вигляді інтегралу: . Вона рівна кількості джоулів, що переноситься сигналомза часТ. Її можна представити у вигляді вектора S_m в заданому базисі. Амплітудне значення цього вектора визначається через амплітуди відповідних базисних функцій. Можна показати, що для довільного кінцевого набору сигналів {S_i(t)} (i=1…M), де кожен елемент реалізований в часі на проміжку Т, кожен елемент можна виразити як лінійну комбінацію:

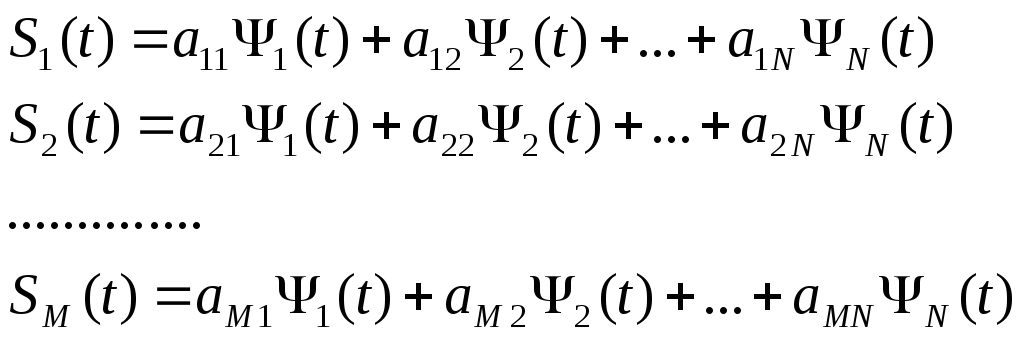
Або в більш компактній формі:

(ІІІ)

Коефіцієнти .(IV)

a_ij визначають як коефіцієнти біля базисних функцій в заданому розкладі. Базисні функції вибираються з точки зору зручності запису інформаційних сигналів S_i. Шумові сигнали є випадковими величинами, які задають певне відхилення від реального інформативного значення, тому у векторній формі відображення вони створюють певну сукупність значень, які певним чином розсіяні навколо основного інформаційного сигналу.

Для відображення сигналів у векторній формі також застосовують вектори S_j та S_k, які називають сигналами- прототипами або опорними сигналами, що належать набору М. Приймач визначає апріорі положення кожного з векторів- прототипів в М- мірному просторі, тоді сигнал шуму можна зобразити вектором розсіювання , тоді вектори- прототипи будутьта. В приймач надходить певний векторний сигнал, який можна виразити певною лінійною комбінацією базисних функцій. Завдання детектора полягає у визначенні найбільшої правдоподібності прийнятого сигналу до певного сигналу- прототипу. В геометричному просторі це зводиться до визначення найближчої відстані між прийнятим сигналом і сигналом- прототипом. Нормоване значення енергії дляS_i сигналу можна виразити через ортогональні компоненти:

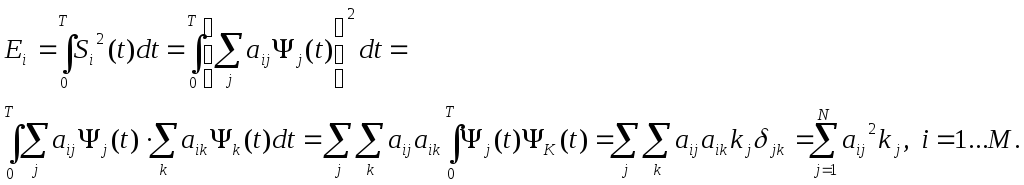
Останній вираз, що зв’язує енергетичне значення сигналу S_i з сумою квадратів коефіцієнтів ортогонального розкладу називають частковим випадком т. Персеваля.

В ортонормованому базисі результуюче значення визначається виключно коефіцієнтом розкладу: .

§7.3 Узагальнене перетворення Фур’є. Представлення білого шуму через ортогональні сигнали. Співвідношення сигнал- шум у цифровій системі передачі даних

Співвідношення, які включають визначення ортогонального базису ((І)-(IV)) називають узагальненим перетворенням Фур’є. При звичайному перетворенні Фур’є, функції включають тільки синусоїдальні та косинусоїдальні функціонали. В узагальненій формі вони можуть бути довільними. Головне, щоб вони задовільняли першій умові ортогональності. Тоді довільну функцію, що описує інформаційний сигналS можна представити з допомогою лінійної комбінації базисних ортогональних сигналів. Тоді для детектування інформаційних сигналів можна використовувати співвідношення для прямокутного ефлідового простору. Якщо інформаційний сигнал описується не ортогональним набором, то при детектуванні вводиться поняття зважуваного значення.

Сигнали адитивного білого шуму, їх ще записують AWGN, як і довільний інший сигнал можна записати у вигляді довільної комбінації ортогоналів сигналів. Для зручності розгляду його можна розділити на дві складові: .

- вона описує проекції компонент шуму на всі координати ψ_j.

- описує шумові сигнали поза використовуваним ортогональним базисом. можна розглядати як ефективне значення шуму, що відсіюється детектуючим пристроєм, тоді як- це та складова, яка впливає на процес детектування. Тоді шумовий сигнал можна записати у вигляді ряду:.

Таким чином ефективне значення шумового сигналу може бути описане вектором . Можна записати:, при чому всі складові- лінійно незалежні.

Основним критерієм якості цифрової системи зв’язку, як і для аналогових застосувань, є співвідношення середньої потужності сигналу відносно середньої потужності шуму- (SNR- параметр). В цифрових системах частіше застосовують нормоване значення SNR- параметра у вигляді відношення ,E_b- енергія біта. Її можна описати як потужність сигналу, помножена на час його передачі: . ПідN₀ розуміють спектральну густину потужності шуму. Її можна визначити як потужність N₀ = N/W. Оскільки час передачі біта інформації і швидкість передачі бітів- обернено взаємозв’язані, то величину T_b можна замінити на 1/R_b: .

Аналогічно, враховуючи, що швидкість передачі біта може бути виражена через узагальнену швидкість R, можна одержати значення: .