Практичне завдання

1. Ознайомитися з вимірювальною схемою і перевірити її готовність до роботи.

2. Виконати вимірювання температурної залежності електропровідності від кімнатної температури до Т = 110 ⁰C з інтервалом 15-20 ⁰С.

3. Дані вимірювань та обчислень записати в таблицю:

Vt

t0,C

T,K

V0

Vx1

Vx2

Vxcp



lg( )

103/T

4. Побудувати графік lg() = f(10³/T) і, користуючись ним, визначити ширину забороненої зони Е_g.

Розрахункові формули

Визначення питомої електропровідності за даними експерименту здійснюється за формулою:

= (l/S  1/R_o)(V₀/V_x),

де: l – відстань між потенціальними зондами зразка (см);

S –площа поперечного перерізу (см²);

 R_o – величина еталонного опору (Ом);

 V_x –  спад напруги на частині зразка між потенціальними зондами;

V_o –  різниця потенціалів на еталонному опорі.

Формула для визначення ширини забороненої зони з температурної залежності електропровідності:

E_g= - 0,397 [lg()/(10³/T)].

Контрольні запитання

1. Як класифікують речовини за величиною електропровідності чи питомого опору?

2. Чим відрізняється напівпровідник від металу і напівпровідник від діелектрика щодо їх енергетичної структури?

3. Пояснити графік залежності (Т) напівпровідника і металу.

4. Які домішки називають акцепторними, а які донорними?

5. Опишіть механізми провідності в донорному і акцепторному напівпровідниках. Що таке змішана провідність? Що таке компенсований напівпровідник?

6. Який напівпровідник називається власним? Наведіть вираз температурної залежності електропровідності для власного напівпровідника.

7. Поясніть графік залежності n(Т) у напівпровіднику донорного і акцепторного типу з погляду переходів електронів між енергетичними зонами і рівнями. Що таке область виснаження домішок?

8. Поясніть, чому температурну залежність питомої електропровідності для визначення ширини забороненої зони напівпровідника будують у координатах lg =f(10³/T ).

9. Які параметри можна знайти з вимірювань питомої електропровідності?

10.  Поясніть методику знаходження E_g із температурної залежності електропровідності в області власної провідності.

ЛАБОРАТОРНА РОБОТА №2

Дослідження температурнОї залежності коефіцієнта холла у власному напівпровіднику. Визначення ширини забороненої зони напівпровідника

Мета роботи: експериментальне дослідження температурної залежності коефіцієнта Холла та визначення за даними вимірювань ширини забороненої зони напівпровідника.

Ефект Холла у напівпровідниках  найважливіший з гальваномагнітних явищ. З його допомогою можна досить просто визначити тип провідності напівпровідника та його важливі параметри: концентрацію носіїв заряду та їх рухливість. Температурні залежності останніх дозволяють знаходити ширину забороненої зони, енергію активації домішкових рівнів та їх концентрацію, визначати механізми розсіювання носіїв заряду.

Датчики Холла (прилади, дія яких базується на ефекті Холла) широко використовують для вимірювання магнітної індукції, НВЧ потужності та ін.

Виникнення ефекту Холла є результатом спільної дії зовнішніх електричного та магнітного полів на заряджену частинку. Під дією електричного поля заряджена частинка набуває швидкості напрямленого руху (дрейфова швидкість). Дрейфова швидкість електронів направлена проти електричного поля, а дрейфова швидкість дірок співпадає з його напрямком. Для пояснення ефекту Холла слід розглянути вплив магнітного поля на дрейфовий рух носіїв заряду. На заряджену частинку, що рухається з дрейфо-воюшвидкістю в магнітному полі з індукцією ,_, діє сила Лоренца:

. (1)

Якщо електричне поле спрямувати вздовж осі х, а магнітне – вздовж осі у, то сила Лоренца буде вектором, перпендику-лярним до цих векторів і, тобто направлена вздовж осіz (рис. 1).

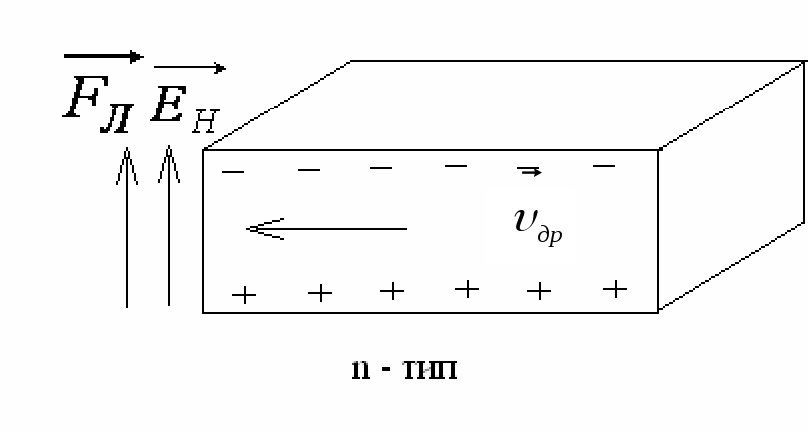
Рис.1. Виникнення поля Холла в електронному і дірковому напівпровідниках.

Відповідно до виразу (1), напрямок сили Лоренца буде однаковим як для електронів, так і для дірок, оскільки крім різного напрямку

швидкостей, вони мають і різні знаки зарядів. Під дією сили Лоренца електрони й дірки будуть відхилятися до однієї й тієї ж грані зразка, до якої вектор напрямлений по нормалі. Холлівське поле, яке виникає в результаті цього відхилення, буде мати різну полярність для напівпровідників n- i p-типу провідності.

Величина напруженості холлівського поля пов’язана з гус-тиною струму , що протікає у зразку, і магнітною індукцією співвідношенням:

. (2)

Коефіцієнт пропорційності R_H у співвідношенні (2) називається коефіцієнтом Холла. Холлівське поле, яке виникає внаслідок накопичення зарядів на гранях зразка, буде мати різну полярність для напівпровідника n- і p-типу, що дає можливість використовувати ефект Холла для визначення типу провідності.

Вираз для коефіцієнта Холла в області домішкової (відповідно, донорної та акцепторної) провідності має вигляд:

R_Н  = - A/en (3)

та

R_Н  =  A/ep, (4)

де n і p – концентрації електронів і дірок; A – Холл-фактор (коефіцієнт, величина якого залежить від механізму розсіювання носіїв заряду в кристалічній гратці та ступеня їх виродження). Для діркового напівпровідника коефіцієнт Холла має додатне значення, а для електронного – від’ємне.

Для напівпровідників зі змішаною провідністю R_H має вигляд ,(5)

де  b = _n/_p, а _n і _p – холлівські рухливості електронів і дірок. Як

видно з формули (4), коефіцієнт Холла перетворюється в нуль за умови p = nb² .

Для напівпровідників із власною провідністю n = p = n_i, тому

. (6)

У більшості напівпровідникових матеріалів рухливість електронів більша за рухливість дірок, так що b>1. Тому в області власної провідності коефіцієнт Холла від’ємний.

Форма залежності коефіцієнта Холла від температури досить складна (рис. 2).

Температурну залежність коефіцієнта Холла можна пояснити на основі температурної залежності концентрації носіїв заряду в невиродженому напівпровіднику.

Рис. 2. Типові температурні залежності коефіцієнта Холла

для напівпровідників різного типу провідності.

Якщо взяти зразок p-типу провідності, то в області низьких температур будуть відбуватися теплові переходи електронів із валентної зони на акцепторний рівень. Внаслідок цього у валентній зоні напівпровідника будуть утворюватися рівноважні носії заряду - дірки, тому коефіцієнт Холла буде мати додатний знак. Провідність у цій області температур буде домішковою. Із підвищенням температури відбувається виснаження домішкового рівня і концентрація носіїв заряду, а отже, і коефіцієнт Холла в даному температурному інтервалі від температури не залежать. При високих температурах електрони безпосередньо із валентної зони переходять у зону провідності, і тоді провідність напівпровідника визначається електронами в зоні провідності і дірками у валентній зоні. Така провідність є власною. За рахунок більшої рухливості електронів, ніж дірок, у більшості напівпровідників коефіцієнт Холла в цій області має від’ємний знак. Тому при переході від домішкової до власної провідності відбувається зміна знака коефіцієнта Холла.

Оскільки в області власної провідності коефіцієнт Холла обернено пропорційний концентрації власних носіїв заряду, яка для невиродженого напівпровідника задається виразом

, (7)

де N_c, N_v – ефективна густина станів, відповідно, в зоні провідності тавалентній зоні і дорівнює

, , (8)

де m_n^* i m_p^* – ефективні маси електронів і дірок, то значення величини R_H може бути записане в такому вигляді:.

. (9)

Побудувавши графік залежності lg(|R_i|T^3/2) від 10³/T, за нахилом кривої в області власної провідності можна обчислити ширину забороненої зони E_g при температурі абсолютного нуля таким же методом, як і за даними електропровідності.

При зміні напрямку зовнішнього електричного чи магнітного поля змінюється напрямок сили Лоренца, а отже, і полярність холлівського поля. Тому ефект Холла є непарним ефектом як стосовно струму, так і магнітного поля. Ця властивість ефекту Холла використовується для усунення так званих паразитних ерс, які мають місце при вимірюванні ефекту Холла.

До них належать:

1. Асиметрія розміщення холлівських контактів, тобто розташування холлівських зондів не на одній еквіпотенціальній поверхні (поверхні рівного потенціалу) за відсутності магнітного

поля. Це призводить до того, що при ввімкненні напруги на холлівських контактах з’являється різниця потенціалів V_о = IΔR, де ΔR – опір ділянки зразка довжиною Δх. При ввімкненні магнітного поля ця різниця потенціалів може змінюватись внаслідок зміни опору зразка в магнітному полі, отже, V_о залежить від магнітноїіндукції . V_о є парною функцією магнітного поля і непарною функцією електричного струму, тобто змінює свою полярність лише при зміні напрямку струму.

2. Виникнення термоерс V_α = αΔТ (ΔТ – різниця температур у точках розміщення холлівських зондів) відбувається при вимірюванні температурних залежностей холлівської ерс внаслідок неоднорідного нагрівання зразка через його недостатнє термостатування. Величина V_α може змінюватись у магнітному полі, тобто V_α = V_α(В). Полярність V_α не залежить ні від напрямку струму, ні від напрямку магнітного поля, тобто вона є парною функцією і струму, і магнітного поля.

3. Гальваномагнітний ефект Еттінгсгаузена, або виникнення поперечного до струму і магнітного поля градієнта температур між точками розміщення холлівських контактів призводить до появи ерс Еттінгсгаузена V_Е  = αΔТ_Е. Причина виникнення цього градієнта температур – розподіл електронів за швидкостями. Поле Холла компенсує поле сили Лоренца лише для носіїв заряду з певною середньою швидкістю. Магнітне поле діє на гарячі електрони (зі швидкістю, більшою за середню) сильніше, ніж на холодні, і тому гарячі електрони відхиляються магнітним полем на одну грань, а повільніші електрони накопичуються на протилежній грані, тобто відбуваєтьсяпросторове розділення носіїв з різними енергіями, а отже, з різними температурами. У результаті обміну енергією носіїв із граткою виникає градієнт температури, і, відповідно, ерс, яка залежить від напрямку струму і магнітного поля так само, як полярність холлівської напруги. Вона додається до неї під час вимірювань і не може бути відділена при зміні напрямку струму чи магнітного поля.

4. Ефект Нернста-Еттінгсгаузена, або поперечний термомагнітний ефект має місце при наявності вздовж зразка градієнта температур. При розміщенні такого зразка у взаємно перпендикулярних електричному і магнітному полях носії дифузійного потоку, що виникає внаслідок градієнта температур, також будуть відхилятись у результаті дії сили Лоренца. На холлівських зондах з’явиться ерс Нернста-Еттінгсгаузена, яка є парною за струмом і непарною за магнітним полем.

Ефектові Холла супутні також деякі інші ефекти, які є паразитними при вимірюваннях ерс Холла, але вони роблять менший внесок при вимірюваннях. Методика усунення паразитних ерс базується на тому, що холлівська напруга та паразитні ерс мають різну парність за струмом і магнітним полем. Тому, виконавши чотири вимірювання напруги на холлівських зондах при різних напрямках струму і магнітного поля, можна позбутись усіх паразитних ерс, парність яких не збігається з парністю холлівської напруги.

МЕТОДИКА ЕКСПЕРИМЕНТУ

Найпростішим щодо технічного виконання, а внаслідок цього і найпоширенішим методом дослідження ефекту Холла є метод постійного струму і постійного магнітного поля. Величину коефіцієнта Холла визначають на основі вище наведеної формули (2). Безпосереднім експериментальним завданням у цьому випадку є вимірювання ерс Холла, що виникає при розміщенні в магнітному полі зразка, вякому протікає електричний струм. Також необхідно визначити величину густини цього струму. Зразки виготовляють правильної геометричної форми, наприклад у вигляді циліндра або прямокутного паралелепіпеда. Для під’єднання зразка в електричну схему на його торці розміщують омічні контакти і до них припаюють струмопровідні дротинки. Через зразок від зовнішнього джерела живлення пропускають постійний струм I, для визначення якого послідовно зі зразком в електричне коло під’єднують еталонний опір із відомим значенням R₀. Оскільки через зразок та еталонний опір проходить однаковий струм, то, використовуючи закон Ома, можна записати

_, (10) де R₀ – значення еталонного опору; V₀ – спад напруги на еталонному опорі.Величину визначають з виразу

, (11)

де S – площа поперечного перерізу зразка.Для визначення на бічні поверхні зразка, між якими виникає холлівське електричне поле, встановлюють два зонди (рис. 3).

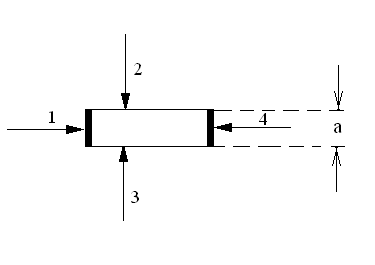
Рис. 3. Розміщення контактів на зразку при вимірюванні коефіцієнта Холла: 1, 4 – струмові електроди; 2, 3 – зондові контакти для вимірювання ерс Холла.

Тоді напруженість холлівського поля може бути визначена так:

^, (12)

де а – розмір грані (див. рис. 3).

Для визначення коефіцієнта Холла здійснюють чотири вимірювання холлівської напруги при різних напрямках струму і магнітного поля, щоб позбутися всіх пара-зитних ерс, парність яких не збігається з парністю холлівської напруги.

Припишемо двом можливим напрямкам електричного струму і магнітного поля знаки « +» і «-». Тоді отримаємо чотири можливих комбінації напрямків струму і магнітного поля, які можна позначити: I⁺B⁺; I^¯B⁺; I^¯B^¯; I⁺B^¯. Напруги, що знімаються з холлівських зондів і відповідають цим комбінаціям, позначимо через V_x1; V_x2; V_x3; V_x4 відповідно. Полярність напруг необхідно фіксувати при кожному вимірюванні.

Запишемо всі розглянуті вище ерс при різних напрямках струму і магнітного поля, враховуючи їх полярність. Отримаємо чотири варіанти:

I⁺ B⁺ V = V_Н + V_о + V_α + V_Е + V_{Н- Е},

I⁺ B^ˉ V = -V_Н + V_о + V_α - V_Е - V_{Н- Е},

I^ˉ B^ˉ V = V_Н - V_о + V_α + V_Е - V_{Н- Е},

I^ˉ B⁺ V = -V_Н - V_о + V_α - V_Е + V_{Н- Е}.

Якщо врахувати зміну полярності різних складових, що входять у вимірювану напругу при зміні напрямку струму та магнітного поля, то для отримання ерс Холла з результатів вимірювань необхідно змінити знак на протилежний перед результатами першого і третього (або другого і четвертого) вимірювань і знайти середнє значення за таким виразом:^._.

_. (13)

Зазначимо, що розглянутий метод визначення ерс Холла дозволяє виключити всі паразитні ерс, крім ерс Еттінгсгаузена V_E, яка має таку ж парність за струмом і магнітним полем, як і ерс Холла. Однак величина V_E значно менша за ерс Холла, тому нею можна знехтувати.

Тепер можемо визначити величину коефіцієнта Холла R_H на основі виразу (7), враховуючи співвідношення (8) і (9):

. (14) Якщо для величин, що входять у формулу (14), використовувати одиниці ви-мірювання Вольт, метр, Ампер, Тесла, то отримаємо R_H у м³/Кл. Якщо ж використовувати несистемні одиниці  Вольт, сантиметр, Ампер, Гаусс, а R_H - у см³/Кл, то, враховуючи зв’язок між одиницями: 1м=10²см; 1Т=10⁴Гс, отримаємо:

(15)

Необхідно зазначити, що точність вимірювання величини холлівської напруги суттєво залежить від співвідношення геометричних розмірів зразка і розміщення зондових контактів. Для того, щоб струмові контакти не закорочували холлівські, відношення довжини зразка до його висоти повинно задовольняти умову l/h ≥ 3, а холлівські зонди повинні розміщуватись на відстані від торців не менше 1,5h.