Практичне завдання

1. Ознайомитись із вимірною схемою і перевірити її готовність до роботи.

2. Провести виміри температурної залежності коефіцієнта Холла від кімнатної температури до t = 110⁰C з інтервалом 15-20⁰ С.

3. Дані вимірів та обчислення записати в таблицю:

HIHIHIHI

Vt

T0,C

T,K

Vо

Vx1

Vx2

Vx3

Vx4

Vc

RH

lg(RHT3/2)

103/T

4. Побудувати графік lg(R_HT^3/2) = f(10³/T) і, користуючись ним, визначити ширину забороненої зони Е_g..

Формули для обчислення параметрів:

Визначення коефіцієнта Холла за даними експерименту проводиться за формулою:

R_H=10⁸(R_ob/H)*(V_x/V_o),

де b – товщина зразка(см); H – напруженість магнітного поля (Ерс),  R_o – величина еталонного опору (Ом);  V_x – Холлівська

напруга; V_o – різниця потенціалів на еталонному опорі.

Формула для визначення ширини забороненої зони із температурної залежності ефекта Холла:

E_g= 0.397*[lg(R_HT^3/2)/(10³/T)]

Контрольні запитання

1. Поясніть, як виникає ефект Холла. Чому його можна використовувати для визначення типу провідності напівровідника?

2. Чому напрямок сили Лоренца не залежить від типу провідності напівпровідникового зразка?

3. Наведіть вираз для коефіцієнта Холла в області домішкової, змішаної та власної провідностей.

4. Чим визначається знак коефіцієнта Холла в області домішкової, власної та змішаної провідності?

5. Поясніть графік залежності R_Н(T) для напівпровідників p- та n-типу провідності.

6. Чим визначається величина Холл-фактора?

7. Які паразитні ерс виникають при  вимірюванні  ефекта  Холла?

8. Чому при вимірюванні електропровідності комутують струм, а при вимірюванні коефіцієнта Холла – струм і магнітне поле?

9. Які параметри напівпровідників можна визначити з вимірювань коефіцієнта Холла?

10.  Які вимоги висуваються до розмірів холлівського зразка та роташування контактів на ньому?

ЛАБОРАТОРНА РОБОТА №3

Дослідження температурної залежності холлівської рухливості та концентрації носіїв заряду

Мета роботи: Експериментальне дослідження температурної залежності електропровідності й коефіцієнта Холла та визначення за даними вимірювань температурної залежності концентрації носіїв заряду і холлівської рухливості.

За відсутності зовнішнього електричного поля електрони в кристалі здійснюють лише тепловий рух. Протягом деякого часу (час вільного пробігу) електрон рухається приблизно прямолінійно і рівномірно. Потім у результаті взаємодії з кристалічною граткою він різко змінює напрямок свого руху. Такий процес зміни імпульсу називається процесом розсіювання.

При розміщенні напівпровідникового зразка у зовнішньому електричному полі з напруженістю електрони під дією поля отримують додаткові швидкості. Виникає напрямлений потік електричних зарядів (електричний струм). Дрейфова швидкість, тобто середня швидкість впорядкованого руху носіїв заряду в електричному полі, пропорційна напруженості електричного поля.Дрейфова рухливість , за визначенням, є дрейфовою швидкістю, яку має електрон в електричному полі з одиничною напруженістю:

=. (1) З теорії кінетичних явищ у твердому тілі відомо, що

, де τ – час релаксації; m* – ефективна маса носія заряду.

Як правило, дрейфова швидкість набагато менша, ніж швидкість теплового руху носія заряду у твердому тілі. Тому середній час вільного пробігу носія τ визначається швидкістю його теплового руху, і прикладене електричне поле тільки несуттєво змінює цю величину.

Якщо у кристалі переважають заряджені частинки одного типу, то густина електричного струму дорівнює:

=en=en. (2)

Оскільки, згідно із законом

=, (3)

де  – питома електропровідність речовини, то:

 = en. (4)

При зміні знака заряду носія заряду e одночасно змінюється і знак рухливості, тому  не залежить від знака заряду частинок. Оскільки коефіцієнт Холла в області домішкової провідності визначається за формулою R_Н = A/en, то з (4) можна отримати, що  = _Н /R_H , а холлівська рухливість пов’язана із дрейфовою через Холл-фактор А:

_H = А. (5)

Вимірявши питому електропровідність  і коефіцієнт Холла R_H в області домішкової провідності досліджуваного напівпровідника, можна знайти холлівську рухливість носіїв заряду зі співвідношення:

_H  = R_Н. (6)

Різниця між дрейфовою та холлівською рухливостями відображає той факт, що вони пов’язані з реагуванням носіїв заряду на різні дії. Дрейфова рухливість описує дію електричного поля на носії, коли на кожен із них діє одна й та ж сила. Холлівська рухливість вводиться, коли на дрейфуючі носії діє сила Лоренца, величина якої для кожного носія залежить від його енергії. Отже, чим сильніша дисперсія часу релаксації від енергії τ(Е), тим більше відрізняються ці два види рухливості один від одного, а величина А – від 1.

Електрон, рухаючись в ідеальному кристалі, при температурі абсолютного нуля не відчував би розсіюючих зіткнень і рухався б вільно. Однак у реальному напівпровіднику обов’язково присутні різні види дефектів, що порушують періодичність кристала. Центрами розсіювання можуть бути теплові коливання гратки, атоми та іони домішок, власні точкові дефекти  вакансії та міжвузлові атоми, дислокації, межі двійників та ін. Якщо температура кристала відмінна від нуля, атоми гратки хаотично коливаються, внаслідок чого порушується ідеальна періодичність кристалічного потенціалу. Виникає розсіювання на коливаннях гратки,  яке  тим  сильніше,  чим  вища  температура  кристала, а отже, і амплітуда коливань. Рухливість при такому виді розсіювання спадає пропорційно Т^-3/2. Цей механізм розсіювання є домінуючим в області високих температур. У цій температурній області величина рухливості практично не залежить від концентрації домішок.

Якби в кристалі були відсутні домішки і недосконалості, зі зниженням температури рухливість носіїв збільшувалась би до безмежності. Але в області низьких температур починає домінувати розсіювання на іонізованих домішках, і рухливість зменшується.

При зростанні температури рухливість при розсіюванні на іонізованих домішках зростає пропорційно Т^3/2. Це зумовлено тим, що середня швидкість теплового руху носіїв заряду збільшується з підвищенням температури. Чим більша швидкість електрона, тим менше буде спотворюватись його траєкторія при русі біля домішкового атома, тому що зменшиться час взаємодії електрона з домішкою. Отже, рухливість носіїв заряду зростатиме. Залежність рухливості в широкому температурному інтервалі з урахуванням розсіювання носіїв заряду на іонізованих домішках і теплових коливаннях гратки буде визначатися формулою . (7)

Розглянемо температурну залежність величини  з урахуванням наведених типів механізмів розсіювання, які у напівпровідниках є основними (рис. 1).

При розсіюванні на нейтральних центрах рухливість носіїв заряду не залежить від температури.

Якщо напівпровідник не містить домішок у великих кількостях, його температура достатньо висока і концентрація електронів не дуже велика, то головну роль тут відіграють процеси розсіювання на теплових коливаннях гратки і Холл-фактор дорівнює A = 3/8 = 1,18.

Якщо напівпровідник містить значну кількість заряджених домішок, то в області низьких температур, коли розсіювання на

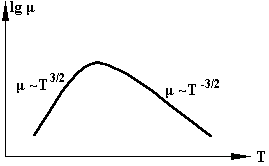
Рис.1. Температурна залежність рухливості носіїв заряду

в напівпровідниках.

коливаннях гратки мале, головним видом розсіювання є розсіювання на заряджених домішках і А = 315/512  1,93.

У напівпровіднику з великою кількістю носіїв заряду (вироджений напівпровідник), а також у випадку сильних магнітних полів А  1.