21.12. Електропровідність напівпровідників

а). Власна провідність. У напівпровіднику при T=0 валентна зона заповнена по усім енергетичним рівням, а верхня, вільна, знаходиться на відстані до 2 - 3 eB. При T>0 електрони валентної зони можуть подолати заборонену зону і перейти у вільну, утворюючи вакансію у валентній зоні. При накладанні зовнішнього електричного поля, у напівпровіднику виникає струм, носіями якого будуть електрони у зоні провідності та електрони у валентній зоні при наявності вакансій. При цьому валентні електрони не відриваються від атомів, а переходять від одного атома до атома з незаповненим зв'язком у напрямкові протилежному напрямкові вектора напруженості зовнішнього електричного поля. Розглянемо, наприклад, кристал германію Ge (див.на Мал.231).

Г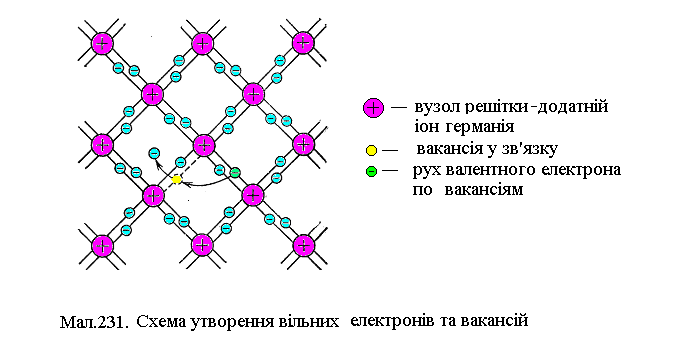ерманій належить до 4 групи та має 4 валентних електронів, які зв'язують атоми у кристалі. Теплової енергії kT при T>0 достатньо, щоб якийсь із цих 4-х електронів відірвався від атома (покинув валентну зону) та став вільним у межах кристала (перейшов до вільної енергетичної зони). Направлений рух електронів у валентній зоні під дією зовнішнього поля означає, що валентні електрони сусідніх атомів можуть займати незаповнений зв'язок. Крім цього вільні електрони можуть знову ж зайняти вакансію. При наявності у валентній зоні порівняно невеликого числа вакансій з концентрацією N_p нам потрібно було б розглядати рух великого числа електронів по ним. Щоб усунути ці труднощі в теорії введені р-квазічастинки - ‘дірки’, за допомогою яких розглядається рух валентних електронів по вакансіям.

Діркам приписується додатній заряд, рівний по величині заряду електрона, та ефективна маса m_p*, яка визначається положенням вакансій у валентній зоні. Дірки та електрони під дією зовнішнього електричного поля мають відповідні, залежні від напруженості поля E, середні швидкості направленого руху V_p та V_e. Ці швидкості, у першому наближенні, пропорційні величині напруженості поля E

V_p=u_pE , V_e=u_eE , (1)

де коефіцієнти пропорціональності u_p та u_e називаються рухливістю дірок та електронів відповідно. У чистому напівпровіднику дірки валентної зони та електрони зони провідності створюють власну провідність із густиною струму

(2)

де - концентрація та рухливість електронів, а- дірок.

Поклавши

,

власну провідність напівпровідника можна записати так

. (3)

Розрахунки квантової статистики для концентрацій n_e електронів у зоні провідності та концентрації n_p дірок такі залежності від температури

, (4)

де

.

У цих виразах _e та _p -хімічні потенціали електронів та дірок. При Т=0 K хімічні потенціали можна визначити через ширину забороненої зони,яка розділяє валентну зону та зону провідності

. (5)

Справді, при переході електрона з валентної зони в зону провідності виникають два носії струму: електрон та дірка і на їх створення потрібна енергія рівна енергії активації E. При цьому на один носій струму припадає енергія , що й визначає величину хімічного потенціалу. Вираз (5) показує, що рівень Фермі розташований посередині забороненої зони. З підвищенням Т цей рівень трошки зміщується ближче до зони провідності

. (6)

Рухливість електронів та дірок визначається розсіюванням їх на теплових коливаннях кристалічної решітки (фононах) і

. (7)

За величиною рухливості електронів та дірок можуть суттєво відрізнятися. Так величина і становить для ІnSb - 59 (= 7,7), для Gе - =2 (=0,38) та для Sі =3,4 (=0,135).

З урахуванням (3)-(6) можна одержати остаточний вираз для власної провідності  та питомого опору  чистого напівпровідника у вигляді

. (8)

У (8) ₀ та ₀ залежать від Т, але ця залежність повільніша експоненціальної, тому, у невеликих інтервалах Т, ₀ та ₀ можна вважати сталими.