21.8. Електропровідність металів

а). Рівняння динаміки руху електронів. Метод ефективної маси

Для дослідження руху електронів у періодичному полі кристала достатньо записати та розв'язати рівняння другого закону Ньютона

_, (1)

де m-класична маса електрона, - сила створена зовнішнім електричним, а- кристалічним полями. Але для цього потрібно описати у явному вигляді, що ми зробити не в змозі. З огляду на це, було запропоновано досліджувати рух електрона у кристалі методом ефективної маси. В основі методу лежить корпускулярно-хвильовий дуалізм електрона: псі-функція електрона у кристалі являє собою хвильовий пакет з несучою частотою, яка є функцією хвильового вектора. У такому випадку покладаємо, що швидкість електрона V співпадає із груповою швидкістю V_гр хвильового пакета

(2)

і може бути визначена через його енергію наступним чином

. (3)

Під дією зовнішньої сили електрон придбаває імпульс, який зв’язаний з нею другим законом Ньютона

. (4)

Величину прискорення електрона можна визначити з (3) таким чином

. (5)

Враховуючи (4), маємо

. (6)

Вираз (6) можна представити у вигляді рівняння другого закону Ньютона для електрона

,

де

(7)

так звана ефективна маса електрона. Цю масу можна тлумачити як міру інертності електрона до дії зовнішньої сили , у просторі періодичного потенціального поля кристала. У такому випадку властивості криcталічного поля закладаються у залежність енергії Е від хвильового вектора . Ця залежність визначається розв'язком відповідного рівняння Шредінгера. Підсумовуючи розглянуте, можна стверджувати, що метод ефективної маси дає можливість розглянути рух електрона у кристалічному полі під дією зовнішнього електричного поля, як рух вільного електрона, згідно рівняння (6).

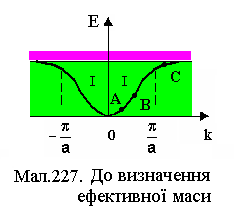
Знаючи залежність Е від k, можна визначити та характер руху електрона. Наприклад, для одновимірного кристала біля дна першої дозволеної зони (точка А) залежність Е відk квадратична (див.на Мал.227) і співпадає з такою для вільного електрона, тобто:

 m.

У точках перегину кривої (точка В) друга похідна від Е(k)

Це означає, що електрони, які знаходяться посередині енергетичної зони, беруть обмежену участь в електропровідності. На верхніх енергетичних рівнях, під стелею першої зони Брилюєна (точка С), Е має максимум:

Це означає, що під дією сили електрони набувають прискорення, протилежного напрямкові цієї сили.

Б). Квантова теорія електропровідності металів

Як показують квантово-механічні розрахунки величина провідності  металів з уведенням ефективної маси , по вигляду, співпадає із класичною провідністю

, (8)

де n- концентрація вільних електронів із зарядом e,  - час релаксації (фактично час вільного пробігу).

Щодо температурної залежності , то до Т=50 К вона та співпадає з дослідними даними, на відміну від класичної теорії, де.

Зазначимо, що опір направленому рухові електронів під дією зовнішнього електричного поля пов'язаний з розсіюванням їх на тепловому коливальному русі вузлів кристалічної решітки (фононах) та її дефектах, домішках, вакансіях і механічних неоднорідностях.