2.2 Графический метод решения задач линейного программирования

Данный метод применяется для решения задач, содержащих не более трех переменных, чаще всего для задач с двумя переменными. Он базируется на следующих моментах:

• множество допустимых решений задачи выпукло, в линейном случае оно представляет собой конечный или простирающийся в бесконечность многоугольник;

• целевая функция достигает своего оптимального значения в вершине области. Если она принимает это значение в двух вершинах области, то оптимум достигается в любой точке отрезка, соединяющего эти вершины;

• направляющий вектор (вектор нормали) перпендикулярен прямой функции цели и всегда указывает направление ее возрастания.

Схему применения графического метода проиллюстрируем на конкретном примере, рассматривая три этапа:

• построение области допустимых решений;

• построение направляющего вектора и определение оптимальных точек;

• нахождение оптимальных значений переменных и целевой функции.

Найти максимальное и минимальное значение функции

при ограничениях

І этап. Построение области допустимых решений

1. Каждому неравенству ставим в соответствие равенство, геометрическим образом которого является прямая линия. Для ее построения достаточно двух точек.

• - эта прямая пройдет через точки (2; 0) и (0; 3).

  0	3
  2	0

• - эта прямая пройдет через точки (-3; 0) и (0; 2).

  0	2
  – 3	0

• - эта прямая пройдет через точки (4; 0) и (0; -4).

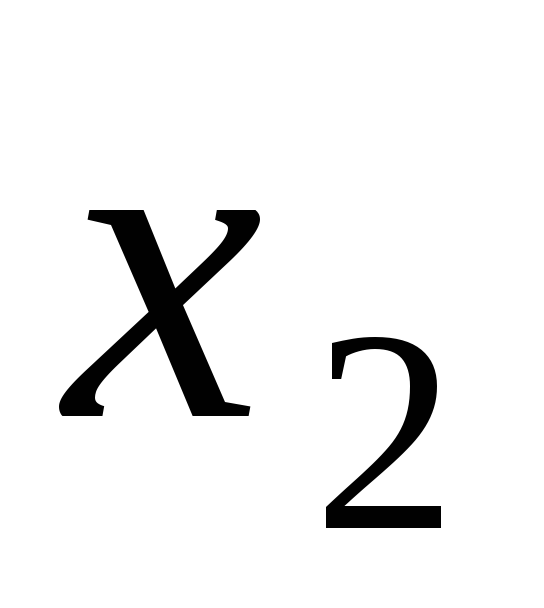
  0	– 4
  4	0

• - эта прямая пройдет через точки (7; 0) и (0; 4).

0	4
7	0

2. Каждая прямая делит плоскость на две полуплоскости, в одной из которых будет справедливо соответствующее неравенство. Чтобы установить, точки какой полуплоскости будут обеспечивать выполнение неравенства, необходимо взять произвольную точку и ее координаты подставить в неравенство. Если для этой точки неравенство выполнилось, то решением неравенства будет та полуплоскость, в которой брали точку. Если неравенство для выбранной точки не выполнилось, то его решением будут точки второй полуплоскости. Рассматривая поочередно все ограничения, получим область, в которой будут справедливы все неравенства, - это и есть область допустимых решений.

Неравенства и означают, что область будет находиться в первой четверти. В нашем случае областью допустимых решений являются точки пятиугольника .

ІІ этап. Определение оптимальных точек

1. Направляющий вектор проводят из начала координат в точку с координатами, равными коэффициентам целевой функции, то есть в точку . Он всегда указывает направление возрастания функции, направление убывания целевой функции будет противоположным.

2. Перпендикулярно направляющему вектору на области допустимых решений проводят прямую (она показана пунктиром).

3. Если в задаче требуется найти максимум, прямую перемещают параллельно в сторону стрелки направляющего вектора до последней точки области – эта точка и будет точкой максимума. В примере наибольшее значение достигается в вершине .

4. Если требуется найти минимум, то прямую перемещают параллельно в противоположную сторону до последней точки области. В данном случае наименьшее значение достигается в вершине .

ІІІ этап. Нахождение оптимальных значений

Чтобы найти переменные, обеспечивающие экстремум, необходимо решить систему уравнений тех прямых, на пересечении которых располагается точка экстремума

а) находим	б) находим

Таким образом, найдены максимальное и минимальное значение функции, все промежуточные значения будут достигаться в других точках области допустимых значений.

Замечание 1. Если прямая функции окажется параллельной какой-нибудь стороне многоугольника ограничений, то в этом случае задача имеет бесчисленное множество решений: координаты любой точки этой стороны многоугольника (в том числе и вершины) будут решением задачи.

Замечание 2. Если область решений не ограничена, то задача или не имеет решения, или целевая функция может принять только максимальное или только минимальное значение, или задача имеет бесконечное множество решений.