
16_07_15_Konspekt_Lektsiy_dlya_PGS
.pdf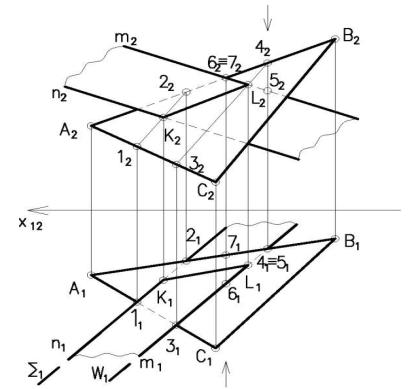
Пересечение двух плоскостей. Две плоскости пересекаются по прямой линии, поэтому для ее построения достаточно найти две точки, одновременно принадлежащие двум плоскостям.
Рисунок 4.18. Пересечение двух плоскостей
Рассмотрим несколько случаев построения линии пересечения двух плоскостей.
1-й случай – пластины непрозрачные заданы с нахлестом (рис. 4.18). Задача сводится к нахождению точек пересечения прямых m и n с плоскостью ά (∆ АВС). Соединив точки пересечения К и М получим линию пересечения плоскости ά (∆ АВС) с плоскостью β (m//n). Видимость определяется по конкурирующим точкам.
2-й случай – плоскости заданы на некотором расстоянии, что не дает возможность определить линии пересечения двух плоскостей первым способом. В этом случае используется метод плоскостей-посредников.
Алгоритм решения задачи (рис. 4.19):
1.Заданные плоскости ά и β рассекаем вспомогательной плоскостью посредником ε;
2.Определяем линию пересечения 1-2 плоскости ά с плоскостью σ и линию пересечения 3-4 плоскости β с плоскостью ε;
70
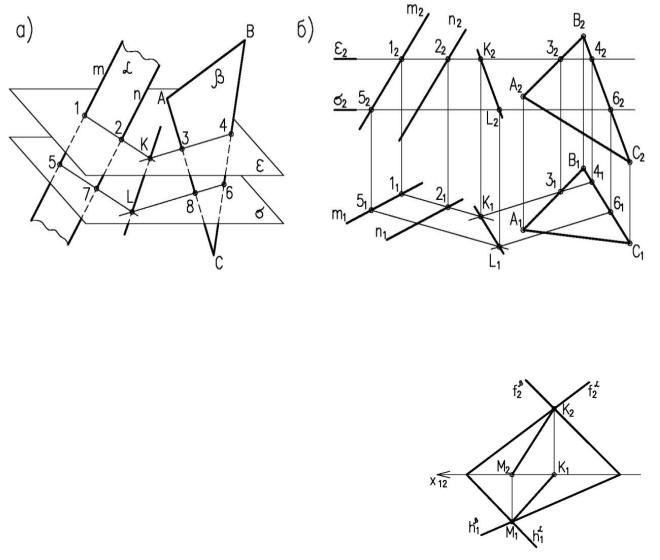
3.Определяем точку К – точку пересечения линий 1-2 и 3-4, принадлежащую плоскостям ά и β;
4.Аналогичным образом находим точку L с помощью плоскости посредника σ;
5.Соединив две точки К и М, получим линию пересечения двух плоскостей ά и β. Видимость при этом не определяется.
Рисунок 4.19. Пересечение двух плоскостей
3-й случай – пересекающиеся плоскости общего положения заданы следами пересекающимися в пределах чертежа (рис. 4.20).
В данном случае в качестве плоскостейпосредников могут быть использованы плоскость проекций П1 и П2.
Рисунок 4.20. Пересечение двух плоскостей
Пересечение гранной поверхности с прямой
Рассмотрим задачу на определение точек пересечения прямой с многогранником на следующем примере (рис. 4.21).
71
Построить точки пересечения прямой ℓ с поверхностью наклонной трехгранной призмы. Последовательность решения следующая:
1.Через прямую ℓ проводим вспомогательную фронтально-проецирующую плоскость σ2.
2.Строим линию пересечения плоскости σ2 и призмы. Сечением является треугольник 1, 2, 3.
3.Определяем точки пересечения прямой ℓ с треугольником сечения (точки L и М).
4.Определяем видимость прямой ℓ.
Рисунок 4.21. Пересечение прямой с трехгранной призмой
Общий алгоритм построения линии взаимного пересечения поверхностей
При пересечении поверхностей образуется линия, которая называется линией взаимного пересечения поверхностей. Эта линия принадлежит одновременно двум поверхностям. Поэтому ее построение сводится к определению точек одновременно принадлежащих обеим поверхностям. Для нахождения таких точек используется в общем случае
метод вспомогательных секущих поверхностей.
Сущность способа заключается в следующем. Пусть задано две поверхности σ и ψ, как показано на рис.
4.22.
Рисунок 4.22. Схема взаимного пересечения поверхностей
72
Общий алгоритм построения линии пересечения поверхностей:
1.Введем вспомогательную поверхность Ф.
2.Строим линии пересечения поверхности Ф с поверхностями σ и ψ (a и b).
3.Определяем точки пересечения К и М построенных линий пересечения a и b.
4.Многократно повторяя эту операцию, найдем ряд точек, принадлежащих одновременно двум поверхностям.
5.Соединяем последовательно точки с учетом видимости.
В качестве посредников могут быть приняты как поверхности, так и плоскости, но целесообразно выбирать такие, которые дают наиболее простые линии пересечения с заданными поверхностями.
Взаимное пересечение двух поверхностей
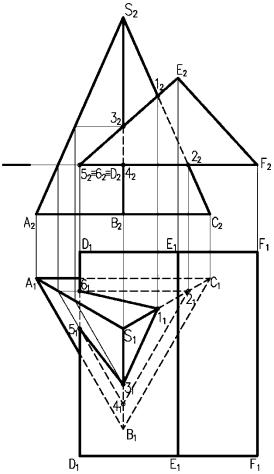
Метод дополнительных плоскостей-посредников. Пересечение двух многогран-
ников. Для построения линии пересечения двух многогранников необходимо определить точки пересечения ребер первого многогранника с гранями второго, затем ребер второго с гранями первого. Полученные точки соединить отрезками прямой с учетом видимости. На рис. 4.23 заданы поверхности трехгранной призмы DEFD'E'F' и трехгранной пирамиды SABC. Так как призма фронтально-проецирующая, фронтальная проекция линии пересечения совпадает с гранями призмы, поэтому необходимо построить только горизонтальную проекцию. Для этого определяем точки пересечения ребер пирамиды с гранями призмы. Ребро SС пересекает грани призмы в точках 1 и 2, ребро SB– в точках 3 и 4, ребро SA не пересекает призму. Затем определяем точки пересечения ребер призмы с гранями пирамиды. По чертежу видим, что только ребро DD' пресекает поверхность пирамиды. Для определения то-
Рисунок 4.23. Пересечение двух многогранников
73
чек пересечения 5 и 6 через ребро DD' проводим горизонтальную плоскость, которая пересекает пирамиду по треугольнику. Точки 5 и 6 получаем, как пересечение DD' с построенным треугольником. Полученные точки соединяем с учетом видимости. Видимой считается тот отрезок прямой, который принадлежит двум видимым граням поверхностей.
Как видим, линия пересечения двух многогранников представляет собой пространственную ломаную линию.
В том случае, когда обе гранные поверхности общего положения, последовательность соединения точек вызывает затруднение. Поэтому для соединения точек используется диаграмма Ананова – условные развертки поверхностей.
Пересечение гранной и кривой поверхности. Линия пересечения гранной и кривой
поверхности, представляет собой пространственную кривую линию, с точками излома на ребрах многогранника. Поэтому сначала определяем точки пересечения ребер многогранника с кривой поверхностью, а затем промежуточные точки и соединяем их с учетом видимости. На рис. 4.24 заданы поверхности трехгранной призмы и кругового конуса.
Так как призма фронтальнопроецирующая, фронтальная проекция линии пересечения совпадает с проекцией боковых граней призмы, поэтому необходимо построить только горизонтальную проекцию линии пересечения.
Сначала определяем точки пересечения ребер призмы АА', ВВ', СС' с поверхностью конуса, а затем находим промежуточные точки, принадлежащие линиям пересечения. Для нахождения точек пересечения, используем горизонтальные плоскости посредники, так как они пересекают конус по окружностям, а призму по прямым линиям. Как видим, в данном случае линия пересечения распадается на две отдельные части.
Рисунок 4.24. Пересечение гранной и кривой поверхности
74
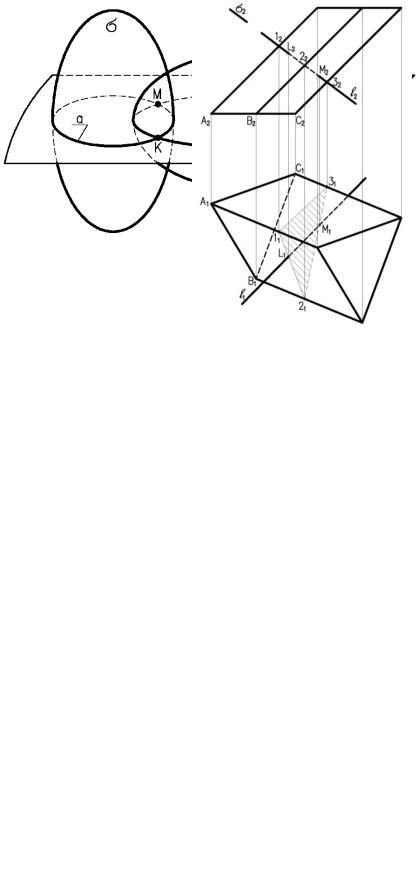
Пересечение двух кривых поверхностей. Линия пересечения двух кривых поверх-
ностей, представляет пространственную кривую линию. Поэтому для ее построения необходимо определить ряд точек принадлежащих этой линии.
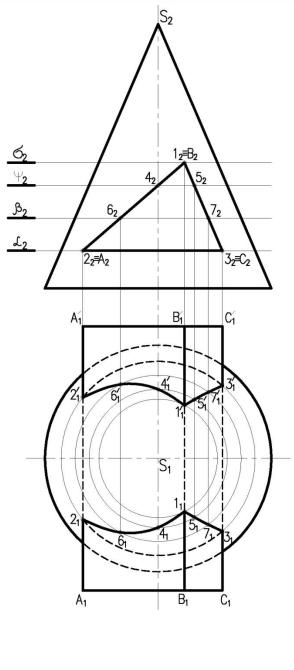
На рис. 4.25 заданы поверхности конуса и сферы. Точки строятся при помощи горизонтальных плоскостей посредников, которые рассекают обе поверхности по окружностям.
Обязательно находим опорные точки, к которым относятся высшая и низшая точки линии пересечения и точки границы видимости. Так как оси поверхностей лежат в одной фронтальной плоскости, контурные образующие поверхностей пересекаются в точках 1 и 2 – это и будет высшая и низшая точки. Точки границы видимости лежат на экваторе сферы, поэтому точки 3 и 3' находим с помощью вспомогательной горизонтальной плоскости, проходящей через центр сферы. Она рассекает сферу по экватору, а конус по параллели радиуса R.
Взаимно пересекаясь, они и дают точки 3 и 3', фронтальную проекцию определяем по вертикальной линии связи на плоскости δ. Затем берем еще две вспомогательные плоскости, расположенные выше и ниже плоскости δ2, выполняя аналогичные построения, определяем точки 4 и 4', 5 и 5'.
Полученные точки соединяем с учетом видимости.
Рисунок 4.25. Пересечение двух кривых поверхностей
Метод дополнительных секущих сфер для построения линии пересечения поверхностей вращения
Способ вспомогательных секущих сфер применяется при следующих условиях:
1.Пересекающиеся поверхности являются поверхностями вращения.
2.Оси этих поверхностей пересекаются.
75
3. Оси поверхностей параллельны одной из плоскостей проекций.
Перед рассмотрением этого способа разберем понятие соосных поверхностей. Соосными называются поверхности вращения, имеющие общую ось. Соосные поверхности пересекаются по окружностям перпендикулярным оси вращения.
На рис. 4.26 приведены некоторые из них. Именно то, что поверхности пересекаются по окружностям, которые проецируются в линии, и используется в методе сфер.
Рисунок 4.26. Пересечение поверхностей вращения методом сфер
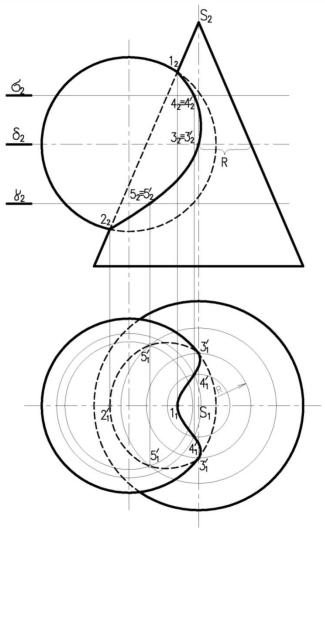
Рассмотрим пример на рис. 4.27. Даны поверхности вращения – конус и цилиндр. Так как оси лежат в одной плоскости, можно определить точки пересечения контурных образующих в точках 1 и 2, как в предыдущем примере. Однако, для нахождения промежуточных точек, вспомогательные секущие плоскости не подходят, т.к. горизонтальные плоскости рассекут цилиндр по эллипсам, фронтально-проецирующие
– конус по эллипсам. А сам эллипс строить непросто. Поэтому именно в этом случае удобно использовать в качестве посредников – сферы. За центр вспомогательных сфер принимается
точка пересечения осей заданных поверхностей. Рисунок 4.27. Пересечение поверхностей вращения методом сфер
76
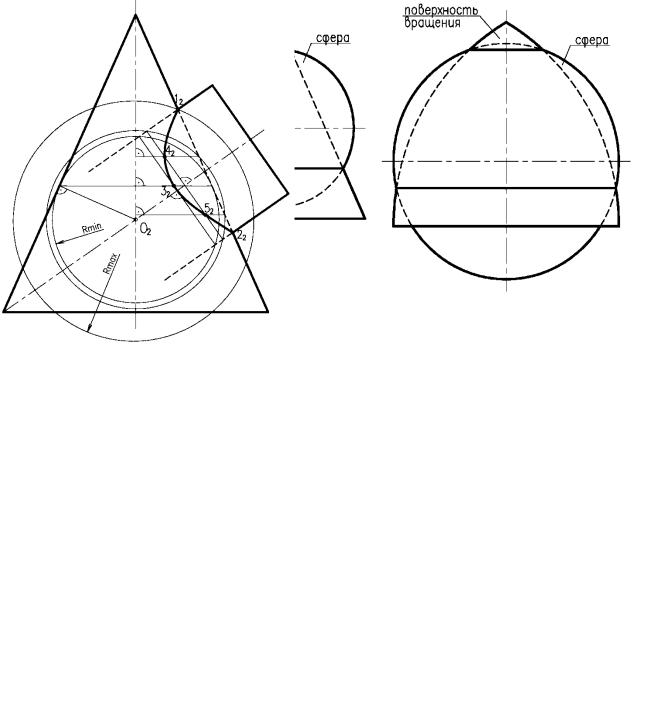
Далее необходимо определить, размеры радиусов вспомогательных секущих сфер. Максимальный радиус сферы Rmax – это расстояние от центра сфер до наиболее удаленной точки пересечения контурных образующих (в данном случае точка 1). Минимальный радиус сферы Rmin – радиус сферы, которая вписана в одну из поверхностей, а другую пересекает. В данном случае минимальная сфера вписана в конус. Минимальная сфера касается поверхности конуса по окружности, а цилиндр пересекает по окружности. Нужно иметь ввиду, что проекции окружностей пересечения перпендикулярны осям вращения. Эти две окружности пересекаются в точке 32. Фактически таких точек две, они совпадают на фронтальной проекции. Для построения промежуточных точек берем вспомогательные сферы радиусов в пределах от Rmin до Rmax. Они пересекают и поверхность цилиндра, и поверхность конуса по окружностям, которые пересекаясь дают промежуточные точки. Полученные точки соединяются плавной линией. Здесь построена только фронтальная проекция. Для построения горизонтальной проекции, если это необходимо, точки строят как лежащие на окружностях полученных радиусов.
Теорема Гаспара Монжа
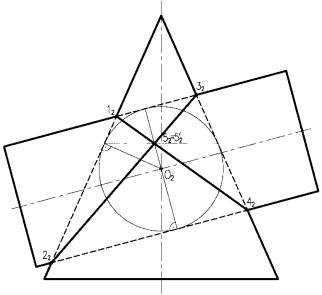
Рассмотрим вариант, когда минимальная сфера касается двух поверхностей вращения (рис. 4.28). В этом случае для построения линии пересечения поверхностей используется теорема Г. Монжа, которая формулируется так:
Если две поверхности вращения второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания.
В соответствии с этой теоремой, линии пересечения конуса и цилиндра описанного около сферы (рис. 4.28), будут плоскими кривыми – эллипсами, фронтальные проекции которых изображаются прямыми 1242 и 2232, проходящими через 5252' – точки линий пересечения окружностей касания.
Рисунок 4.28. Теорема Г. Монжа
77
Лекция 5. Общие сведения о строительных чертежах
∙Чертежи металлических конструкций:
–область применения. Общие сведения;
–общие правила оформления чертежей металлических конструкций;
–чертежи узлов и деталей металлических конструкций.
∙Чертежи железобетонных конструкций:
–область применения. Общие сведения;
–общие правила оформления чертежей железобетонных конструкций.
∙Краткие сведения об основных конструктивных и архитектурных элементах здания:
–вычерчивание плана этажа;
–вычерчивание разреза;
–вычерчивание фасада.
Чертежи металлических конструкций
Область применения. Общие сведения. Наряду с другими материалами в строительстве широко применяют металл. В настоящее время большое распространение получили конструкции из стали и сплавов алюминия. Металл в строительстве применяют в тех случаях, когда по экономическим или техническим соображениям применение других материалов (в частности железобетона) нецелесообразно, например, при сооружении больших мостов, устройстве перекрытий или покрытий зданий с большими пролетами, таких, например, как крытые стадионы, плавательные бассейны, производственные здания. Металлические конструкции большей частью используют в зданиях промышленного и гражданского типа.
Для изготовления массовых строительных конструкций чаще всего применяют стальные прокатные профили. Наибольшее распространение имеют следующие профили прокатной стали: угловая равно- и неравнополочная, двутавр, швеллер.
Основные элементы профиля имеют конкретные названия. Элемент, характеризуемый величиной b в угловой стали, швеллере, двутавре и др. называется полкой. В двутавре и швеллере вертикальный элемент, имеющий высоту h, называется стенкой. Подробное наименование элементов угловой стали и изображение наиболее часто встречающихся профилей проката дано на рис. 5.1.
78
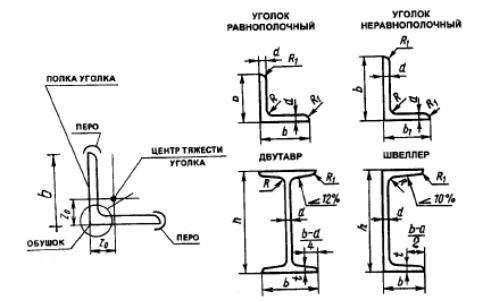
Рисунок 5.1. Прокатные профили
Сведения о размерах, форме и другие данные сортового прокатного профиля различных видов приводятся в специальной таблице сортамента стального проката.
Общие правила оформления чертежей металлических конструкций. Рабочие чер-
тежи металлических конструкций объединяют в комплект под маркой КМ – конструкции металлические зданий и сооружений. Рабочие чертежи марки КМ являются основой для разработки чертежей металлических конструкций деталировочных КМД, для составления смет и расчета необходимого количества металла.
При выполнении чертежей металлических конструкций руководствуются следующими стандартами:
-ГОСТ 2.306-68. Графические обозначения материалов и правила их нанесения на чертежах.
-ГОСТ 2.312-72. Условные изображения и обозначения швов сварных конструкций.
-ГОСТ 2.315-68. Упрощенное и условное изображение крепежных деталей.
-ГОСТ 2.410-68. Правила выполнения металлических конструкций.
-ГОСТ 21.502-2007. Правила выполнения проектной и рабочей документации металлических конструкций.
Всостав чертежей под маркой КМ входят:
-общие данные (заглавный лист);
-схемы расположения элементов металлических конструкций;
-рабочие чертежи металлических конструкций с соответствующими узлами конструкций;
-чертежи отдельных деталей металлических конструкций.
79
