16_07_15_Konspekt_Lektsiy_dlya_PGS

Если хотя бы одна пара одноименных следов различных плоскостей пересекается, то такие плоскости пересекаются между собою по прямой. На рис. 1.33 показано построение линии пересечения плоскостей, заданных следами. Более подробно случай взаимного пересечения двух плоскостей будет рассмотрен в лекции №2.

Рисунок 1.33. Пересечение плоскостей

Две плоскости взаимно перпендикулярны, если одна из них содержит перпендикуляр к другой (рис. 1.34)

Для решения задачи на проведение плоскости, перпендикулярной плоскости ά (∆ВСD), достаточно на прямой m взять произвольную точку А и провести через нее прямую р, перпендикулярную данной плоскости ά. Пересекающиеся прямые m и р образуют плоскость β, которая содержит прямую р, перпендикулярную плоскости άследовательно, плоскости β и ά взаимно перпенди-

кулярны: β (mxp) ┴ ά(∆ВСD) где p┴ ά(∆ВСD).

Рисунок 1.34. Перпендикулярность плоскостей

20

если она параллельна плоскости проекций (рис. 2.2), β– угол наклона к плоскости П2

2. Расстояние от точки к прямой проецируется в натуральную величину, если прямая проецирующая (рис. 2.3).

Рисунок 2.3. Прямая проецирующая

3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рис. 2.4).

Рисунок 2.4. Прямые проецирующие

4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рис. 2.5).

Рисунок 2.5. Прямая проецирующая

5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее

(рис. 2.6).

Рисунок 2.6. Двугранный

угол

22

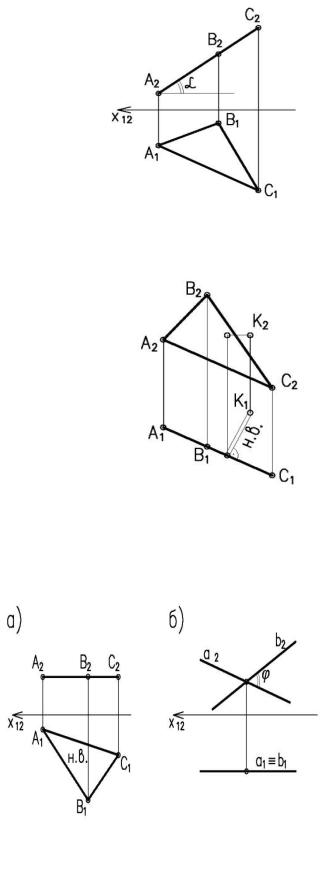
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рис. 2.7).

Рисунок 2.7. Плоскость проецирующая

7. Расстояние от точки к плоскости проецируется в натуральную величину, если плоскость проецирующая

(рис. 2.8).

Рисунок 2.8. Плоскость проецирующая

8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рис. 2.9).

Рисунок 2.9. Плоскость уровня

23

Переход от общего положения геометрической фигуры к частному можно осуществить за счет изменения взаимного положения проецируемой фигуры и плоскостей проекций. Это достигается двумя путями:

-во-первых, перемещением плоскостей проекций в новое положение, по отношению к которому проецируемая фигура, которая при этом не меняет своего положения в пространстве, окажется в частном положении;

-во-вторых, перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве.

Первый путь лежит в основе способа замены плоскостей проекций, второй - способа вращения вокруг проецирующих осей.

Существуют и другие способы преобразования: вращение вокруг линий уровня, плоскопараллельное перемещение, способ совмещения, способ вспомогательного проецирования.

Вообще, всякое построение на комплексном чертеже, отображающее определенные построения в пространстве, и приводящее к образованию новых полей проекций, называется

преобразованием комплексного чертежа.

Решение метрических и позиционных задач

Наиболее выгодным частным положением проецируемой фигуры следует считать:

–положение, перпендикулярное к плоскости проекций – при решении позиционных задач;

–положение, параллельное плоскости проекций – при решении метрических задач.

Метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемыми линейными и угловыми величи-

нами. К метрическим характеристикам относят длины участков линий, величины углов, площадей, объемов и т.п.

Наиболее сложные задачи при решении которых используют как метрические, так и позиционные свойства геометрических фигур, называют комплексными.

Все метрические задачи сводят к двум видам а) задачи на определение расстояния между двумя точками;

б) задачи на определение величины угла между двумя пересекающимися прямыми.

24

Четыре основные задачи преобразования проекций

Задача 1 (ЛН). Прямую общего положения преобразовать в линию уровня (одно преобразование).

Задача 2 (ЛТ). Прямую общего положения преобразовываем в проецирующую (два преобразования).

Задача 3 (ПЛ). Плоскость общего положения преобразовать в проецирующую (одно преобразование).

Задача 4 (ПН). Плоскость общего положения преобразовать в плоскость уровня (два преобразования).

Для решения задач предлагается следующая последовательность:

∙Представить, в каком отдельном положении должны находиться геометрические объекты для того, чтобы ответ задачи можно было получить на одной из проекций очень просто (например, применить простое измерение). Некоторые из подобных положений приведены на рис. 2.10.

∙Отметить, какое из четырех положений ЛН, ЛТ, ПЛ или ПН необходимо для непосредственного решения задачи.

∙Преобразованием проекций привести задачу к этому отдельному положению. Выделить на преобразованной проекции ответ задачи.

Рассмотрим два основных способа преобразования комплексного чертежа.

Способ замены плоскостей проекций (ЗПП)

Сущность способа состоит в том, что одна из плоскостей проекций (П1 или П2) заменяется новой плоскостью проекций так, чтобы геометрическая фигура, занимая общее положение в системе плоскостей проекций П1 – П2, в новой системе плоскостей проекций (например, П1 – П4), оказалась бы в частном положении (т.е. меняем П2 на П4), (рис. 2.10). При этом не должен нарушаться принцип метода Монжа, то есть новая плоскость проекций, например, П4, должна быть перпендикулярна остающейся плоскости проекций П1.

25

Рисунок 2.16. Третья основная задача преобразования проекций в пространстве

Рисунок 2.17. Третья основная задача преобразования проекций

29