
16_07_15_Konspekt_Lektsiy_dlya_PGS
.pdf
Рисунок 1.8. а) Точка С на наглядном чертеже отрезка АВ б) Точка С на комплексном чертеже отрезка АВ
Следом прямой называется точка пересечения прямой с плоскостью проекций. В со-
ответствии с этим, прямая может иметь горизонтальный (Н), фронтальный (F), профильный (P) следы.
Для примера рассмотрим порядок нахождения фронтального следа F прямой АВ на чертеже (рис. 1.9).
Рисунок 1.9. Следы прямой
10
1. Горизонтальная проекция A1B1 продлевается до пересечения с осью ОХ; в точке пересечения находим горизонтальную проекцию фронтального следа F1.
2. Из F1 проводим вертикальную линию связи до пересечения с фронтальной проекцией A2B2, также продленной соответствующим образом. Точка пересечения является фронтальным следом прямой, совпадающим со своей фронтальной проекцией F ≡ F2.
Способы задания плоскости
Плоскостью называется поверхность, которая образуется при движении прямой линии параллельно самой себе по неподвижной направляющей прямой.
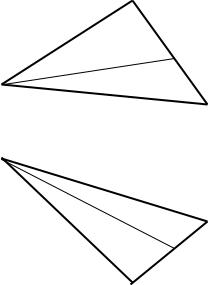
Плоскость можно определить симплексом, т.е. тремя не принадлежащими одной прямой точками, и алгоритмом задания текущей ее точки М (рис.1.10). Точка М (М1, М2)
в плоскости треугольника АВС строится с по-
мощью прямой А1. Точка А принадлежит |
|
|
|
|
|
C2 |
|||
|
|
|
|
|
|
|
|
|
|
плоскости АВС, как вершина этого треугольни- |
|
|
|
|
|
|
|
|
|
ка, точка 1 принадлежит прямой ВС. Тогда вся |
|
|
M2 |
|
|
|
12 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
прямая А1 со всеми ее точками (включая М) |
А2 |
|
|
|
|
|
|
|
B2 |
|
|
|
|
|
|
|
|||
принадлежит плоскости. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Плоскость может быть задана: |
|
|
|
|
|
|
|
|
|
- проекциями трех точек, не лежащих на одной |
А1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
прямой, (рис.1.11), или проекциями треуголь- |
|
|
|
|
|
|
|
|
|
ника; |
|
|
M1 |
|
|
|
|
B1 |
|
|
|
|
|
|
|
||||
- проекциями прямой и точки, взятой вне пря- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|||
мой, (рис. 1.12); |
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|||||
|
|
|
|
|
|||||
- проекциями двух пересекающихся прямых, |
|
|
|
|
|
|
|
|
|
(рис. 1.13); |
|
Рисунок 1.10. Задание плоскости |
|||||||
-проекциями двух параллельных прямых, (рис. 1.14);
-проекциями любой плоской геометрической фигуры, (рис.1.15).
11
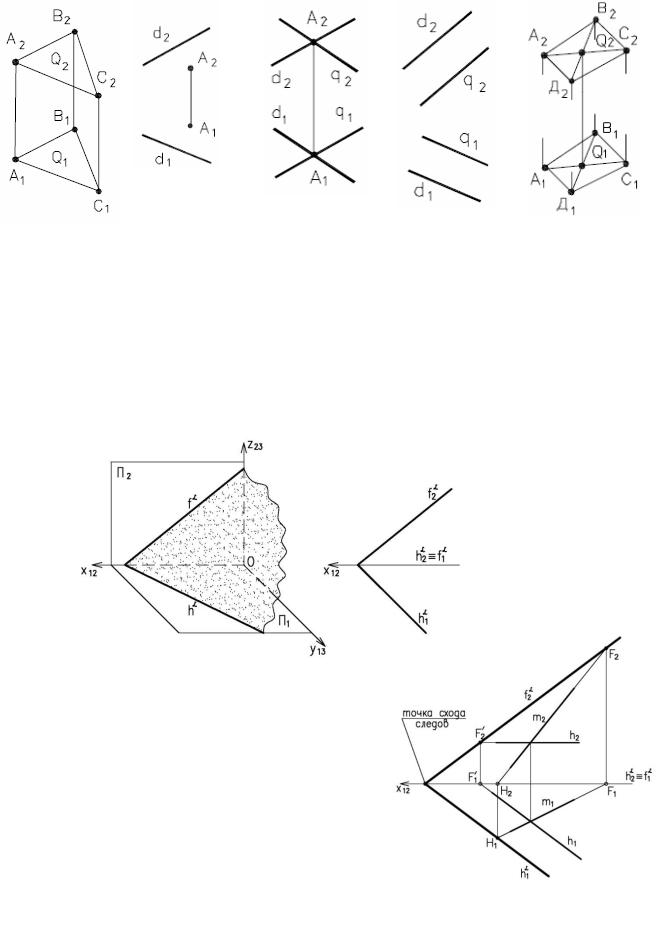
Рисунок 1.11 |
Рисунок 1.12 |
Рисунок 1.13 |
Рисунок 1.14 |
Рисунок 1.15 |
Рисунки 1.11-1.15. Способы задания плоскости на комплексном чертеже
Все изображенные на рис. 1.11-1.15 плоскости являются плоскостями общего положения. Плоскостью общего положения называется плоскость, не перпендикулярная ни одной из плоскостей проекций.
Плоскость также можно задать следами. Следами плоскости называются линии пересечения плоскости с плоскостями проекций (рис. 1.16).
Рисунок 1.16. Задание плоскости следами
Т.к. следы плоскости – прямые линии, то для |
|
их построения достаточно найти две точки принадле- |
|
жащие им. Если прямые лежат в плоскости, то их сле- |
|
ды лежат на следах плоскости. для построения следов |
|
плоскости достаточно построить следы двух прямых |
|
лежащих в этой плоскости (рис. 1.17). |
|
Фронтальным следом плоскости ά называет- |
|
ся линия ее пересечения с фронтальной плоскостью |
Рисунок 1.17. Построение |
|
|
проекций П2. Обозначается фронтальный след буквой fά. |
следов плоскости |
12
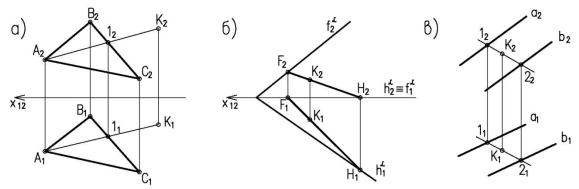
Фронтальная проекция этого следа f2ά совпадает с самим следом, а горизонтальная f1ά лежит на оси х12 .
Горизонтальный след плоскости – линия пересечения с горизонтальной плоскостью проекций П1. Аналогично горизонтальный след плоскости hά совпадает со своей горизонтальной проекцией h1ά, а его фронтальная проекция лежит на оси X12.
Они имеют общую точку на оси X – точку схода следов.
Точка и прямая на плоскости. Главные линии плоскости
Точка и прямая на плоскости. Признак принадлежности точки плоскости:
Точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости, (рис. 1.18).
Справедливо будет и обратное утверждение, которое можно сформулировать как признак принадлежности прямой плоскости:
Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.
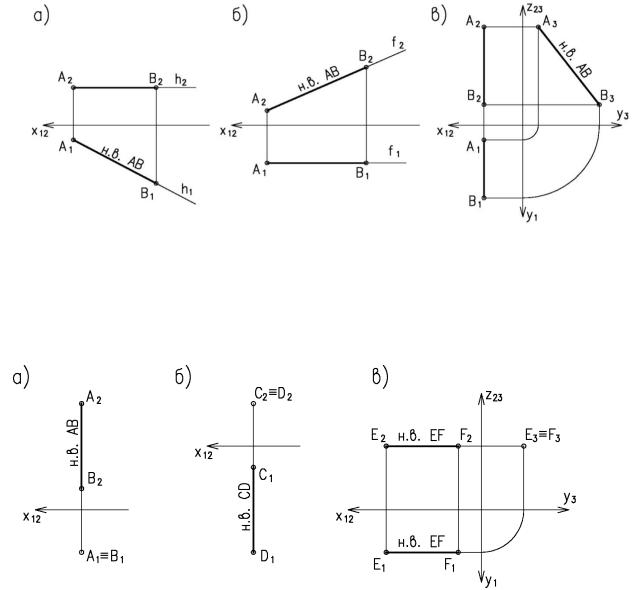
Рисунок 1.18. Примеры построения недостающих проекций точек На рисунке 1.18а. фронтальная проекция точки К (К2) выбрана произвольно в плоско-
сти ά ( АВС). Для построения горизонтальной проекции через К2 проведена прямая, проходящая через точки 12 и А2. Построив горизонтальную проекцию точки 1(11) проведем горизонтальную проекцию прямой А111 и по линии связи найдем на ней проекцию К1.
Главные линии плоскости. В плоскости находится двухпараметрическое множество прямых, среди которых начертательная геометрия выделяет как главные:
1. Горизонталь h плоскости - горизонтальная прямая, принадлежащая плоскости (рис. 1.19).
13

На рис. 1.19 плоскость задана двумя параллельными прямыми a и b. Горизонталь 12 – лежит в этой плоскости, т.к. плоскости принадлежат две её точки 1 и 2.
Фронтальная проекция горизонтали 12 параллельна оси х (h2║х), а горизонтальная проекция горизонтали отражает ее н.в. (h1=н.в.h). На чертежах горизонталь обозначается буквой h (в проекциях h1 и h2).
Рисунок 1.19. Построение горизонтали плоскости
2. Фронталь f плоскости - фронтальная прямая, принад-
лежащая плоскости (рис. 1.20).
На рисунке 1.19 прямая 12 лежит в плоскости, заданной двумя пересекающимися прямыми (плоскость a
Ι b); на чертежах фронталь обозначается буквой f, её го-
ризонтальная проекция параллельна оси х (f1║х), а фронтальная проекция фронтали отражает её н.в. (f2 = н.в. f ).
Рисунок 1.20. Построение фронтали плоскости
3. Линия наибольшего наклона к П1,линия ската плос-
кости - линия, принадлежащая плоскости и перпендику-
лярна ее горизонталям (рис. 1.21).
На рис. 1.21 в плоскости АВС построена горизонталь h, а перпендикулярно её горизонтальной проекции h1 из В1 построена горизонтальная проекции линии ската (л.с.), лежащая также в АВС. По линиям связей из точек пересечения построена фронтальная проекция линии ската.
4. Линия наибольшего наклона к П2 - линия, принад-
лежащая плоскости и перпендикулярна ее фронталям.
Рисунок 1.21. Построение линии ската плоскости
14
Прямые и плоскости частного положения. Проецирование прямого угла
Прямые частного положения. Как уже было сказано выше, прямая, не параллельная ни одной из плоскостей проекций, является прямой общего положения.
Прямые параллельные или перпендикулярные плоскостям проекций называются
прямыми частного положения
Различают два вида прямых частного положения:
- прямые уровня – прямые, параллельные плоскостям проекций; - проецирующие прямые – прямые, перпендикулярные плоскостям проекций.
Прямые уровня (рис. 1.22).
а) горизонтальная прямая – прямая параллельная горизонтальной плоскости П1; б) фронтальная прямая – прямая параллельная фронтальной плоскости П2; в) профильная прямая – прямая параллельная профильной плоскости П3.
Рисунок 1.22. Прямые уровня
Если прямая параллельна плоскости проекций, то она проецируется на эту плоскость в натуральную величину.
Проецирующие прямые (рис. 1.23).
Рисунок 1.23. Проецирующие прямые
15
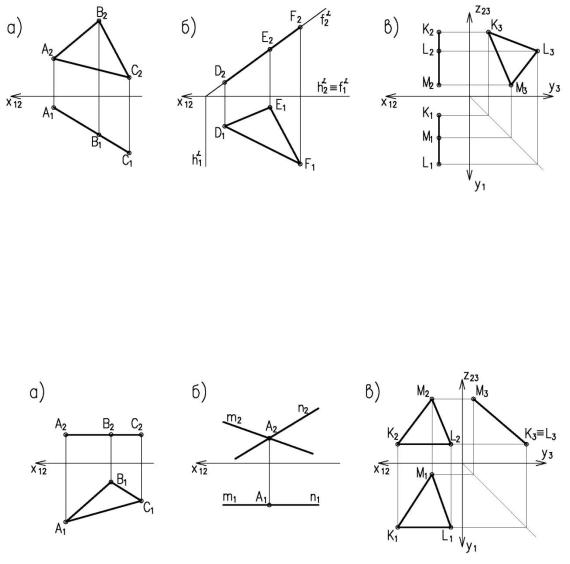
а) горизонтально-проецирующая прямая – прямая, перпендикулярная горизонталь-
ной плоскости проекций П1; б) фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной
плоскости проекций П2; в) профильно-проецирующая прямая – прямая, перпендикулярная профильной
плоскости проекций П3.
Плоскости частного положения. Плоскости, как и прямые, относительно плоскостей проекций могут занимать частное положение. Плоскости, перпендикулярные или параллельные одной из плоскостей проекций, называются плоскостями частного положения.
Плоскости, перпендикулярные одной из плоскостей проекций, называются проеци-
рующими (рис. 1.24).
Рисунок 1.24. Проецирующие плоскости а) горизонтально-проецирующая плоскость ά ( АВС);
б) фронтально-проецирующая плоскость δ ( DEF);
в) профильно-проецирующая плоскость θ ( KLM).
Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня (рис. 1.25).
Рисунок 1.25. Плоскости уровня
а) горизонтальная плоскость уровня β, заданная треугольником АВС;
б) фронтальная плоскость уровня ε, заданная пересекающимися прямыми m и n;
в) профильная плоскость уровня γ, заданная треугольником KLM.
16
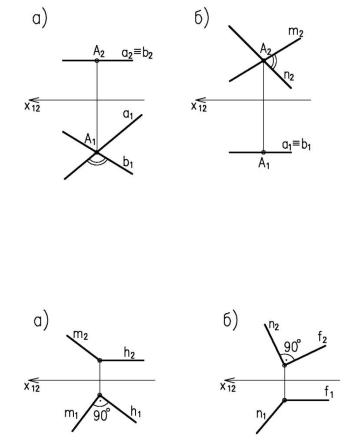
Проецирование прямого угла. Величина угла между двумя пересекающимися прямыми в общем случае на проекциях искажается. В натуральную величину этот угол будет проецироваться в том случае, если плоскость угла параллельна одной из плоскостей проекций. Тогда другие проекции сторон угла совпадают и параллельны оси проекций (рис. 1.26).
Рисунок 1.26. Проецирование прямого угла
Прямой угол проецируется в натуральную величину, если одна из его сторон параллельна одной из плоскостей проекций (рис. 1.27).
Рисунок 1.27. Проецирование прямого угла
Взаимные положения прямых, прямой и плоскости, двух плоскостей
Взаимное положение двух прямых в пространстве. Две прямые в пространстве мо-
гут быть: пересекающимися, параллельными и скрещивающимися. Взаимное положение двух прямых можно установить по эпюру, исходя из соответствующих признаков.
Пересекающиеся прямые. Если две прямые а и b пересекаются в точке N, то точки пересечения одноименных проекций прямых лежат на одной линии связи (рис. 1.28, а).
Параллельные прямые. Если две прямые взаимно параллельны, то их одноименные проекции параллельны: а׀׀b, т.к а1׀׀b1 и а2׀׀b2 (рис. 1.28, б).
17
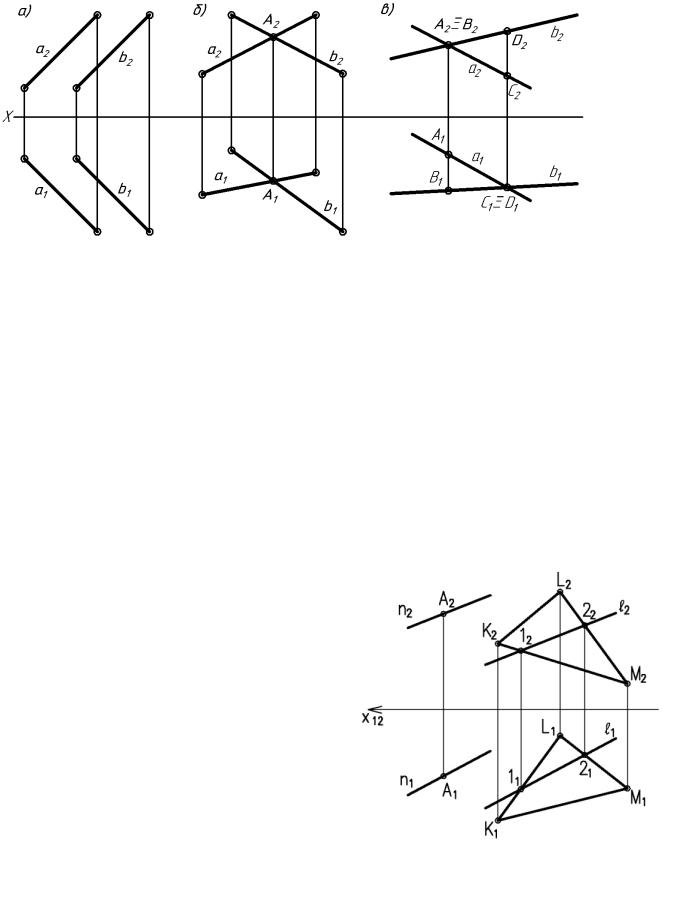
Скрещивающиеся прямые. Если прямые не пересекаются и не параллельны между собой, то точки пересечения их одноименных проекций не лежат на одной линии связи (рис. 1.28, в)
Рисунок 1.28 - Прямые на чертеже: а ) параллельные; б ) пересекающиеся; в ) скрещивающиеся
Точки, лежащие на проецирующей прямой, (рис. 1.28, в). называются конкурирующими. Конкурирующие точки удобно использовать при определении видимости элементов фигур. Из двух конкурирующих точек относительно П1 видимой на П1 является та, высота которой больше. Из двух конкурирующих точек относительно П2 видимой на П2 является та, глубина которой больше. Из анализа проекций конкурирующих точек Na, Nb и Ka, Kb, (рис. 1.28, в), можно сделать вывод, что прямая a проходит перед b и b над прямой a.
Взаимное положение прямой и плоскости. Возможны три случая относительного положения прямой и плоскости:
а) прямая принадлежит плоскости; б) прямая параллельна плоскости;
в) прямая пересекает плоскость (в частном случае под прямым углом).
Прямая принадлежит плоскости, если она проходит через две точки, лежащие в плоскости (рис. 1.29).
Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости.
На рис.1.29 построена фронтальная
Рисунок 1.29. Параллельность прямой и плоскости
18

проекция прямой n, проходящей через точку А и параллельной плоскости ά (∆KLM).
Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция ее перпендикулярна фронтальной проекции фронтали.
На рисунке 1.30 через точку А(А1;А2) проведена прямая, перпендикулярная плоскости ά(∆ВСD).
Вплоскости ά проведены горизонталь h (h1,h2)
ифронталь f (f1,f2) , затем через А1 проведена горизонтальная проекция перпендикуляра p1 под прямым углом к h1, а через точку А2 фронтальная проекция перпендикуляра p2 под прямым углом к f2. Прямые p1 и p2
есть проекции искомого перпендикуляра р.
р ┴ ά → (p1 ┴ h1)+ (p2 ┴ h2)
Общий случай пересечения прямой общего положения с плоскостью общего положения представлен на рис.1.31.
В лекции №4 будет подробно рассмотрено построение точки пересечения прямой n с плоскостью общего положения АВС.
Взаимное положение двух плоскостей. Возможны
два случая относительного положения плоскостей: а) плоскости взаимно параллельны;
б) плоскости пересекаются (в частном случае под прямым углом).
Две плоскости параллельны, если существует пара пересекающихся прямых одной плоскости, соответственно параллельная паре пересекающихся прямых другой плоскости (рис. 1.32).
19
Рисунок 1.30. Перпендикулярность прямой и плоскости
Рисунок 1.31. Пересечение прямой с плоскостью
Рисунок 1.32. Параллельность плоскостей
