4. Кристаллография (1 часть)

4.1. Предмет кристаллографии

Кристаллография - наука о кристаллах и кристаллическом строении вещества.

Геометрическая кристаллография изучает геометрию внешней формы кристаллов и их внутреннее строение.

Физическая кристаллография изучает физические свойства кристаллов в зависимости от их структуры.

Кристаллохимия изучает связь между строением кристаллов и их химическим составом.

В настоящее время предмет кристаллографии охватывает не только кристаллы, но и амфорные, стеклообразные, полимерные и даже жидкие системы. Поэтому современная кристаллография - это область науки, изучающая структуру и свойства конденсированных состояний вещества и их связи с пространственным соотношением межатомных сил.

Кристаллография тесно связана с физикой, химией, минералогией, материаловедением, рентгеноструктурным анализом, математикой, металлургией, машино- и приборостроением, электронной техникой, строительным делом.

В состав различных строительных конструкций и изделий непременно входят кристаллические тела: металлы и сплавы - в металлические конструкции: трубы, котлы и т.д.; силикаты, оксиды металлов, бориды, карбиды, нитриды, силициды и др. - в состав бетонных изделий и композиционных материалов и т.д.

По строению твердые тела условно модно разделить на:

- кристаллические;

- аморфные;

- композиционные.

Примерами кристаллических тел являются природные и искусственные монокристаллы, все металлы и сплавы в обычном состоянии и др. При нормальных скоростях охлаждения все химические элементы в твердом состоянии являются кристаллическими.

Примерами аморфных тел являются стекла, аморфные пленки, полимерные материалы, древесина и пр.

Композиционные материалы сочетают в себе и кристаллические и аморфные составляющие – бетон, железобетон, металлокерамика и пр.

Основным признаком различия кристаллических и аморфных тел – это наличие у первых температуры плавления (кривая 1 на рис.) и отсутствие её у стекол (кривая 2).

Следующий признак – это наличие у кристаллов кристаллической решетки и отсутствие таковой у аморфных тел.

Рис. 4.1. Кривые нагревания кристалла (1)

и аморфного тела (2).

2. Строение кристаллов

"Кристаллос" по-гречески "лед", "кварц". Кристаллыобразуются в природных и лабораторных условиях в виде многогранников со строго закономерным внутренним строением.

Поверхность многогранников ограничена совершенными плоскостями - гранями, которые пересекаются по прямым линиям - ребрам. Точки пересечения ребер образуют вершины. Геометрически правильная форма кристаллов обусловлена строго закономерным внутренним строением. Все кристаллы построены из материальных частиц, геометрически правильно расположенных в пространстве - в кристаллической решетке в виде узлов. Реальные ребра и грани усеяны правильно расположенными атомами, ионами, молекулами.

Ретикулярная плотность _р - количество узлов N_y, приходящихся на единицу площади S поверхности грани кристалла:

_р = N_y / S.

В кристаллах различают ближний и дальний порядок.

Ближний порядок - порядок расположения соседних атомов по отношению к данному.

Дальний порядок - порядок, сохраняемый по отношению не только к ближайшему окружению, но и ко всем остальным атомам, составляющим кристалл.

Монокристалл - это кристалл, в котором атомы сохраняют порядок по отношению ко всему его объему, т.е. в нем имеется как ближний, так и дальний порядок.

Монокристаллы однородны по всему объему и анизотропны, т.е. порядок расположения атомов и физические свойства различны вдоль разных направлений.

Поликристаллы - кристаллические тела, состоящие из хаотически размещенных монокристаллических зерен. Поликристаллы - в целом изотропны, хотя каждое монокристаллическое зерно анизотропно. Аморфные тела также, в основном, изотропны (стекла, жидкости, полимерные некристаллические материалы и пр.).

Под кристаллом в дальнейшем будем иметь ввиду монокристалл.

Кристалл - это дискретная трехмерная периодическая пространственная система частиц.

Макроскопически трехмерная периодичность проявляется в его однородности и способности к самоогранке с строго постоянными двугранными углами и анизотропности свойств. В 1669 г датским ученым Н. Стено, на образцах горного хрусталя (SіO₂), в 1749 г. М.В.Ломоносовым на кристаллах селитры и в 1783 г французским кристаллографом Ж.Роме-де-Лилем на многочисленных кристаллах был установлен закон постоянства углов: углы между соответствующими гранями (и ребрами) во всех кристаллах одного и того же вещества постоянны, независимо от внешней формы кристалла (для одной полиморфной модификации).

Гониометрия - метод измерения углов между гранями кристалла и определения по ним типа кристалла.

Прикладной гониометр Караджо (показан на рис. 4.2). Он служит для определения углов между гранями кристалла.

Рис. 4.2. Гониометр Караджо.

3. Стереографические проекции

Ц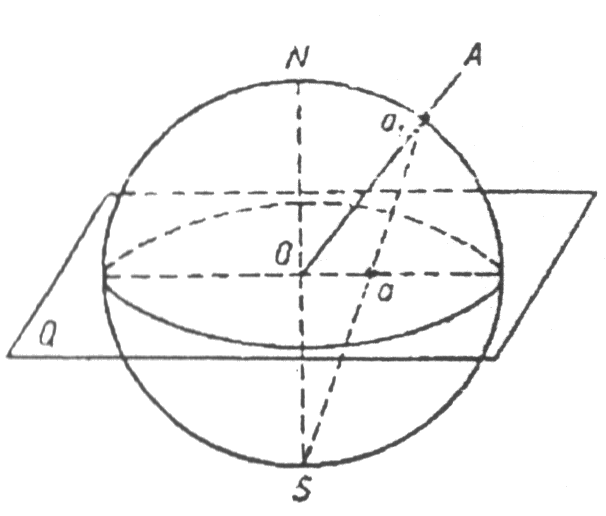ифровой материал, найденный посредством гониометрических измерений, следует изобразить графически на специальных проекциях, которые называют стереографическими. На рисунке 4.3 показаны:

О - центр проекции,

Ш - шар проекции,

Q - плоскость проекции,

К - круг проекции,

NS - ось проекции,

S - точка зрения

Рис. 4.3. Схема построения стереографических проекций

Пример 1. Построение стереографической проекции а направления ОА:

а₁ - точка пересечения направления ОА с шаровой проекцией;

Sа₁ - луч зрения;

а - стереографическая проекция направления ОА.

Таким образом, стереографическая проекция направления изображается точкой:

а - стереографическая проекция направления ОА на плоскость проекций Q;

а' - сферическая проекция.

Пример 2. Стереографическая проекция грани на плоскость Q (рис. 4.4):

ПустьR - плоскость или грань кристалла, тогда

a'b'd' - точки пересечения лучей зрения,

sa', sb', sd' с шаром проекций,

abd точки пересечения лучей зрения,

sа, sb', sd с кругом проекций.

Рис. 4.4.

Вывод: Стереографические проекции плоскости (грани) изображаются дугами.

Пример 3. Проектирование кристалла методом стереографических проекций. На рис. 4.5 показаны:

ABCDA - кристаллический многогранник;

О - центр тяжести;

a₁,b₁,c₁,d₁ точки пересечения нормалей к граням с шаром проекций;

a, b, c, d - стереографические проекции направлений на плоскость проекций Q.

Вывод: грани на проекции

Рис. 4.5. изображаются точками.

Нормали к граням, пересекающим шар в верхней полусфере,проектируются внутри круга проекций, а нормали к граням, пересекающим d нижней полусфере, проектируются вне круга (рис. 4.6).

Неудобство последнего построения заставляет переносить для таких нормалей точку зрения S в северный полюс N. В этом случае проекции нижних граней находятся

Рис. 4.6. внутри круга. Чтобы различить друг от друга проекции нормалей к верхним и нижним граням, первые обозначаются кружками, а вторые – крестиками.

Горизонтальные грани проектируются в центре круга проекций, вертикальные - на круге проекций, косые - внутри круга проекций.