1.3. Основи теорії випадкової похибки

У основі теорії випадкових похибок лежать два припущення:

а) при великій кількості вимірів похибки однакової величини, але різного знаку зустрічаються однаково часто;

б) імовірність появи похибки зменшується зі зростанням її величини (тобто, малі похибки зустрічаються частіше, великі – рідше).

Відповідно до цієї теорії, випадкові похибки підлягають закону нормального розподілу випадкових величин – закону Гаусса. Зміст його полягає в наступному. Припустимо, необхідно виміряти деяку фізичну величину, істинне значення якої нам невідоме. Через випадкові похибки ми, виконавшиокремих вимірювань, замістьодержуємо набір значень. Виявляється, що за допомогою закону розподілу ми, хоча і не можемо вказати точне значення , але можемо знайти, з якою ймовірністювеличинаопиниться всередині заданого числового інтервалу значень. Цей числовий інтервал значень називаєтьсядовірчим інтервалом, а ймовірність того, що результат вимірів потрапляє в заданій довірчий інтервал, називаєтьсянадійною ймовірністю (або надійністю). Рівень значущості дорівнює ймовірності того, що величинане потрапляє у вказаний числовий інтервал.

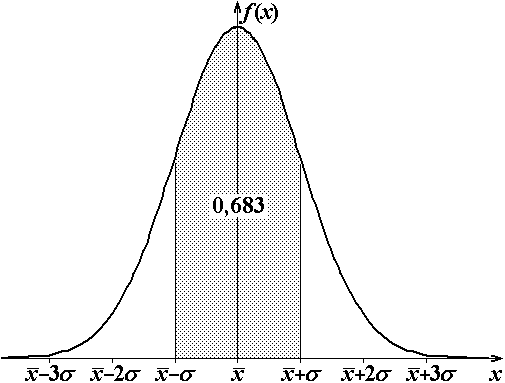
За законом Гаусса, функція густини розподілу випадкових помилок має вигляд (рис. 1.1):

,

(3)

а надійна імовірність потрапляння випадкової величини в інтервалвизначається так:

.		(4)
	Рис. 1.1. Функція розподілу Гаусса.

Тут – набір значень, отриманих при вимірах,– їх середнє арифметичне (математичне очікування), яке вважається найкращою оцінкою істинного значення результату вимірів. За міру розсіювання (розкиду) значень випадкової величини править дисперсія вибірки

,

(5)

що характеризує швидкість зменшення ймовірності появи похибки зі збільшенням величини цієї похибки. Для характеристики розсіювання результатів вимірів користуються поняттям стандартного відхилення або середньої квадратичної (стандартної) похибки окремого виміру , яка дорівнює кореню квадратному з дисперсії вибірки. Величина характеризує середню похибку результату окремого виміру (тобто похибку самого методу вимірів), і обчислюється за формулою:

.

(6)

Величина є мірою вірогідності результату виміру і входить до функції розподілу Гаусса. Гауссова крива має симетричний дзвіноподібний вигляд і характеризується двома параметрами: положенням вершини та“шириною” – відстанню між точками перегину (у яких друга похіднаобертається на нуль). Середнє арифметичнерезультатів окремих вимірів являє собою середину довірчого інтервалу, ахарактеризує вплив випадкових похибок на результат: чим менше, тим вужче крива розподілу похибок окремих вимірів, тим точніше проведений вимір. Однак, з іншого боку, чим більш широким вибирається довірчий інтервал, тим вище ймовірність потрапляння випадкового значенняу цей інтервал.

Для генеральної сукупності результатів вимірів, коли , середнє арифметичнедорівнює істинному значеннювимірюваної величини, якщо, звичайно, результати вимірів не містять систематичної похибки.

Підставивши із (3) в (4), можна розрахувати надійну ймовірністьдля будь-якого довірчого інтервалу. Наприклад, при великій кількості вимірів (), вибравши, одержимо величину надійності(див. рис. 1.1). Це означає, що 68,3% усіх результатів вимірів належать до інтервалу. Аналогічно можна показати, що для інтервалунадійна ймовірність, а длявідповідно. Останнє означає, що за межами довірчого інтервалу півшириноюопиняється лише 0,3% результатів усіх вимірів.

Звідси випливає так зване “правило ”: помилку, що виходить за межі числового інтервалу , вважаютьпромахом (тому що ймовірність її появи всього 0,3%) і виключають результат відповідного виміру з подальшого розгляду. Проте слід нагадати, що  це генеральне середньоквадратичне відхилення (для дуже великої кількості вимірів ), а отже у звичайних вимірах (для невеликої вибірки,) воно залишається невідомим. Тому при малих вибірках“правило ” застосовувати не слід. В інженерній практиці зазвичай вважають достатньою надійність , хоча в деяких випадках (для вимірів, за умовами яких потрібен надзвичайно високий ступінь надійності, наприклад, коли йдеться про життя людей) іноді задають значення надійної імовірності , тобто ступінь ризику (рівень значущості) становить лише 0,1%.

Для обмеженої вибірки середнє значення дещо відрізняється від. Сукупність середніх для деякої кількості вибірок (поокремих вимірів у кожній вибірці) теж описується функцією розподілу Гаусса

.

(7)

де  середнє значення окремої вибірки,  середня квадратична (стандартна) похибка середнього.

Основний сенс усереднення результатів багаторазових вимірів полягає в тому, що середнє значення фізичної величини має меншу випадкову похибку, ніж результати окремих вимірів. Операція усереднення не усуває цілком випадковий характер середнього результату, а лише зменшує ширину інтервалу його невизначеності. Як вказувалося вище, величина характеризує точність даного способу вимірів (міру розсіювання результатів окремих вимірів). Однак, середнє значення фізичної величиниє узагальненням результатів усіхвимірів, тому є всі підстави вважати, що воно є більш надійним, ніж результат кожного окремого виміру. Похибка середнього значення шуканої фізичної величини середня квадратична (стандартна) похибка середнього обчислюється за формулою:

.

(8)

Якщо в науковій роботі наводиться значення похибки і не вказується надійна ймовірність , то мається на увазі стандартна похибка середнього.

Отже, для характеристики величини випадкової похибки необхідно задати два числа: величину самої похибки (півширину довірчого інтервалу ) та величинунадійної ймовірності .

Наведені вище значення надійних ймовірностей для інтервалів,,справедливі лише длягенеральної сукупності вимірів – їхньої нескінченної безлічі. На практиці ж завжди здійснюється обмежена кількість вимірів – мала вибірка. Як же змінюється вірогідність результату в залежності від кількості вимірів?

Англійський математик В.С. Госсет, який публікував свої роботи під псевдонімом Стьюдент, у 1908 році вивів розподіл похибок середніх значень при малій кількості вимірів. Для великих вибірок () цей розподіл практично збігається з розподілом Гаусса. Розподіл Стьюдента дозволяє за надійною ймовірністюта кількістю виміріввизначати відповідний довірчий інтервал. Для цього користуються спеціальною таблицею коефіцієнтів Стьюдента, що залежать відта (табл. 1.1). Коефіцієнти Стьюдента показують, у скільки разів потрібно збільшити стандартний довірчий інтервал, щоб при заданій кількості вимірів одержати необхідну надійність результату. За стандартний приймається довірчий інтервал.

Якщо результати окремих вимірів підлягають нормальному розподілу Гаусса і є однаково точними – тобто виконані на одній апаратурі, з однаковою старанністю і тим самим методом – то випадкова похибка шуканої величини визначають за формулою:

.

(9)

Таблиця 1.1

Коефіцієнти Стьюдента

2	1,84	6,31	12,71	31,82	63,66	212,21
3	1,32	2,92	4,30	6,96	9,92	18,22
4	1,20	2,35	3,18	4,54	5,84	8,89
5	1,14	2,13	2,78	3,75	4,60	6,43
6	1,11	2,02	2,57	3,36	4,03	5,38
7	1,09	1,94	2,45	3,14	3,71	4,80
8	1,08	1,89	2,36	3,00	3,50	4,44
9	1,07	1,86	2,31	2,90	3,36	4,20
10	1,06	1,83	2,26	2,82	3,25	4,02
11	1,05	1,81	2,23	2,76	3,17	3,89
12	1,05	1,80	2,20	2,72	3,11	3,79
13	1,04	1,78	2,18	2,68	3,05	3,71
14	1,04	1,77	2,16	2,65	3,01	3,64
15	1,04	1,76	2,14	2,62	2,98	3,58
16	1,04	1,75	2,13	2,60	2,95	3,54
17	1,03	1,75	2,12	2,58	2,92	3,49
18	1,03	1,74	2,11	2,57	2,90	3,46
19	1,03	1,73	2,10	2,55	2,88	3,43
20	1,03	1,73	2,09	2,54	2,86	3,40
21	1,03	1,72	2,09	2,53	2,85	3,38
22	1,03	1,72	2,08	2,52	2,83	3,35
23	1,02	1,72	2,07	2,51	2,82	3,34
24	1,02	1,71	2,07	2,50	2,81	3,32
25	1,02	1,71	2,06	2,49	2,80	3,30
26	1,02	1,71	2,06	2,49	2,79	3,29
27	1,02	1,71	2,06	2,48	2,78	3,27
28	1,02	1,70	2,05	2,47	2,77	3,26
29	1,02	1,70	2,05	2,47	2,76	3,25
30	1,02	1,70	2,05	2,46	2,76	3,24
40	1,01	1,68	2,02	2,43	2,71	3,17
50	1,01	1,68	2,01	2,40	2,68	3,12
60	1,01	1,67	2,00	2,39	2,66	3,10
	1,00	1,64	1,96	2,33	2,58	2,97

При зі зростанням числа вимірювань коефіцієнти Стьюдента зменшуються мало. Тому виконувати вимірювання більше 30 разів недоцільно це не призведе до скільки-небудь помітного зменшення випадкової похибки результату серії вимірювань.
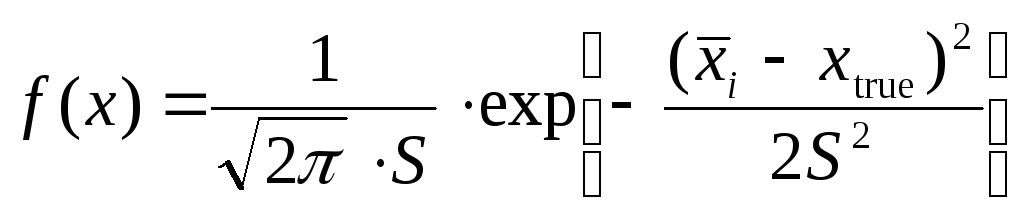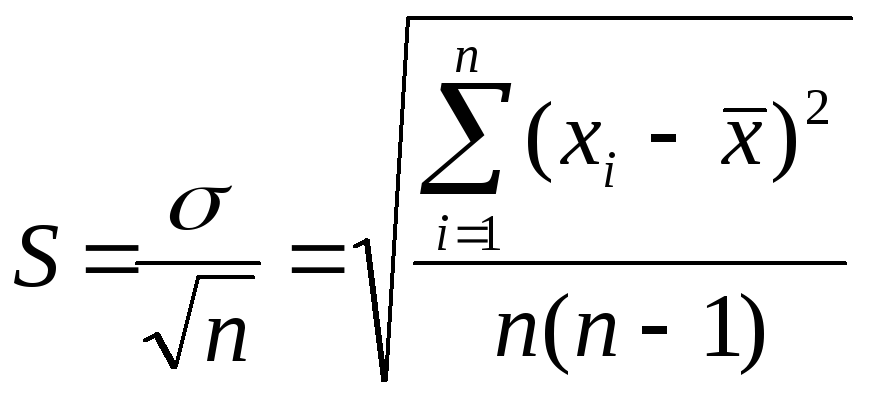