
- •1.1. Матрицы. Операции над матрицами
- •1.2. Определители и их свойства. Правило Крамера решения системы линейных уравнений
- •1.3. Обратная матрица. Решение матричных уравнений
- •1.4. Метод Гаусса решения систем линейных уравнений
- •1.5. Ранг матрицы. Теорема о совместности системы линейных уравнений
- •Глава 2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- •2.1. Векторы на плоскости и в пространстве
- •2.2. Проекция вектора на ось. Скалярное произведение векторов
- •2.3. Векторное и смешанное произведение векторов
- •3.1. Простейшие задачи аналитической геометрии на плоскости
- •3.2. Прямая линия на плоскости
- •3.3. Совместное исследование уравнений прямых
- •3.4.1. Эллипс
- •3.4.2. Гипербола
- •3.4.3. Парабола
- •3.5. Прямая и плоскость в пространстве
- •3.5.1. Плоскость в пространстве
- •3.5.2. Уравнения прямой в пространстве
- •3.5.3. Взаимное расположение двух прямых в пространстве. Угол между прямыми в пространстве
- •3.6. Понятие гиперплоскости. Выпуклые множества
- •Глава 4. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ
- •4.1. Функциональная зависимость и способы ее представления
- •4.2. Элементарные функции. Преобразование графиков функций
- •Глава 5. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ
- •5.1. Числовая последовательность
- •5.2. Предел последовательности
- •5.3. Предел функции. Раскрытие простейших неопределенностей
- •5.4. Замечательные пределы
- •5.5. Сравнение бесконечно малых
- •5.6. Односторонние пределы
- •5.7. Непрерывность и точки разрыва функции
- •Глава 6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- •6.1. Производная функции, ее геометрический и физический смысл
- •6.2. Дифференцирование функций
- •6.3. Дифференциал функции
- •6.4. Производные и дифференциалы высших порядков
- •6.5. Раскрытие неопределенностей. Правило Лопиталя
- •6.6. Основные свойства дифференцируемых функций
- •6.7. Исследование функций
- •6.8. Предельный анализ в экономике
- •Ответы
- •Литература

2.2. Проекция вектора на ось. Скалярное произведение векторов
Проекцией вектора a на ось Ox называется число, обозначаемое ПрOx a и определяемое формулой
ПрOx a =| a | cosϕ ,
где ϕ – угол между вектором a и осью Ox .
Координаты вектора a в ортонормированном базисе равны проекциям вектора a на соответствующие координатные оси:
|
x = ПрOx a , |
y = ПрOy a , z = ПрOz a . |
(2.5) |
Косинусы |
углов |
α = (a ,i ), β = (a , j), γ = (a , j) |
называются |
направляющими косинусами вектора a . Формулы (2.5) можно переписать в виде
x =| a | cosα , y =| a | cos β , z =| a | cosγ . |
|
|
(2.6) |
|||||||||||||||||||
Направляющие косинусы вектора a связаны соотношением |
||||||||||||||||||||||
cos2 α +cos2 β +cos2 γ =1. |
|
|
|
|
|
|
|
|
|
(2.7) |
||||||||||||
Пример 2.4. Вектор a образует углы α =120 |
и β = 60 с осями Ox и Oy |
|||||||||||||||||||||
соответственно. Найти: а) |
угол γ , который образует вектор a с осью Oz , если |
|||||||||||||||||||||
известно, что он острый; б) координаты вектора a , если | a |= 6 . |
||||||||||||||||||||||
Р е ш е н и е :а) из формулы (2.7) находим |
|
|
|
|
|
|
|
|
|
|
||||||||||||
cos2 γ =1 |
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
2 |
|
1 2 |
1 |
. |
||||
−cos2 α −cos2 β = 1− |
2 |
|
− |
|
= |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как угол γ – острый, то cosγ = |
|
= |
|
2 |
|
, и γ = 45 ; |
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
||||||||||||||||
б) координаты вектора a найдем по формулам (2.6): |
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 3 2 . |
|
|||||||||
x = 6 − |
|
= −3, |
y = 6 |
|
|
= 3, |
z = 6 |
|
|
|
|
|||||||||||
2 |
2 |
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Скалярным произведением |
|
векторов |
|
a |
и |
|
b |
называется число, |
||||||||||||||
обозначаемое (a ,b) и определяемое формулой |
|
|
|
|
|
|
|
|
|
|
||||||||||||
(a ,b) =| a || b | cos(a ,b) . |
|
|
|
|
|
|
|
|
|
|
(2.8) |
|||||||||||
37

Основные свойства скалярногопроизведения векторов:
1)(a ,b) = (b ,a) ;
2)(λa ,b) = (a ,λb) = λ(a ,b) ;
3)(a +b ,c) = (a ,c) +(b ,c) ;
4)a 2= (a ,a) =| a |2 ;
5)(a ,b) = 0 a и b ортогональны (при условии | a | ≠ 0 ≠| b | ).
Из определения скалярного произведения следует, что
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a |
,b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
cos(a ,b) = |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(2.9) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a || |
b | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Проекция вектора a |
на ось, |
сонаправленную с вектором b , может быть |
||||||||||||||||||||||||||||||||
найдена по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Пр |
|
a = |
(a ,b) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(2.10) |
||||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
| b | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если векторы a (x1 ; y1 ; z1), b (x2 ; y2; z2 ) заданы координатами в |
||||||||||||||||||||||||||||||||||
ортонормированном базисе, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
(a ,b) = x x |
+ y y |
2 |
+ z z |
2 |
. |
|
|
|
|
|
|
|
|
|
(2.11) |
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 2.5. Найти угол между векторами a (4;−1;−1) и b(2;−2;1) . |
||||||||||||||||||||||||||||||||||
Р е ш е н и е.Согласно формулам (2.9) и (2.11), |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
(a ,b) |
|
|
|
|
4 2 −1 (−2) − |
1 1 |
|
9 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||
|
|
cos(a |
,b) = |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
, |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||
|
|
|
16 +1+1 4 + |
4 +1 |
|
9 2 |
||||||||||||||||||||||||||||
|
|
|
|
|
| a |
|| b |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отсюда (a |
,b) = |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
2.6. |
Найти |
|
длину |
|
вектора |
|
|
a = 2 p −3q , если | p | = 3, | q | = 2 , |
|||||||||||||||||||||||||
(p,q) = π3 .
Ре ш е н и е. Используя свойство 4) скалярного произведения, имеем
| a | = 
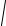 a 2 =
a 2 = 
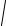 (2 p −3q )2 .
(2 p −3q )2 .
38

Применяя далее свойства 1) – 3), находим
(2 p −3q )2 = 4 p 2−12( p,q) +9q 2 = 4 | p |2−12 | p || q | cos( p,q) +9 | q |2 = = 4 9 −12 3 2 12 +9 4 = 36 .
Следовательно, | a | = 6 .
Пример 2.7. Найти вектор единичной длины, ортогональный векторам m (2;−1;−2) и n (1;1;− 4) .
Р е ш е н и е. |
|
По свойству 5) скалярного произведения для любого |
|||
вектора |
p(x; y; z) , |
ортогонального векторам m и n , |
выполняются равенства |
||
|
|
Кроме того, по условию | p | = |
|
||
( p,m) = 0 |
и ( p,n) = 0. |
x2 + y2 + z2 |
=1. Выражая |
||
скалярные произведения векторов через их координаты, получим систему уравнений
2x − y −2z = 0,x + y −4z = 0,x2 + y2 + z2 =1,
решив |
|
которую, |
|
найдем |
|
два противоположно направленных вектора |
|||||||||
2 |
; |
2 |
; |
1 |
|
и |
|
− |
2 |
;− |
2 |
;− |
1 |
|
, удовлетворяющих условию задачи. |
p1 |
3 |
3 |
|
p2 |
3 |
3 |
3 |
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
|||||
Задачи для самостоятельного решения
2.21.Построить радиус-вектор точки M (4;−3;5) и определить его длину и направление.
2.22.Даны точки A(1;2;3) и B(3;−4;6) . Построить вектор AB , найти его проекции на оси координат и определить его направление.
2.23.Разложить вектор a по базису i , j, k , если он образует с осями
координат Ox, Oy , Oz |
углы α = |
π |
, β = |
2π |
, γ = |
π |
соответственно и |
|
|
4 |
|
3 |
|
3 |
|
|a |= 4
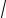 2 .
2 .
2.24.Вектор a образует углы α = 60 и γ = 45 с осями Ox и Oz соответственно. Найти: а) угол β , который образует вектор a с осью Oy , если известно, что он тупой; б) координаты вектора a , если | a | = 2 .
39
2.25.Найти координаты вектора a , образующего равные острые углы с осями координат, если a 2 =12 .
2.26.Найти скалярное произведение векторов a = 6i +3 j −4k и b = 4i −2 j + 2k .
2.27.Известно, что | a |=1, | b | = 2 , (a ,b) = π3 . Найти:
а) (a ,a + 2b) ; |
б)(a −2b ,3a +b) ; |
в) | 2a −3b | . |
|
|
2.28. Найти скалярное произведение |
векторов a и b , |
если |
a = 2 p −3q и |
|
b = 4 p + q , где p и q – единичные ортогональные векторы. |
|
|||
2.29. Найти скалярное произведение векторов a = 2 p + q |
и b = 3p −2q , если |
|||
|p |= 2 , | q |= 3, и ( p,q) = π3 .
2.30.Найти длину вектора a = 4 p −q , если | p |=1, | q |= 
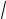 3 и ( p,q) = π6 .
3 и ( p,q) = π6 .
2.31.Найти длины диагоналей параллелограмма, построенного на векторах a = 2 p + q и b = p −2q , где | p |=| q |=1, и ( p,q) = π3 .
2.32.Найти угол между векторами a (−1;4;1) и b(1;2;2) .
2.33.Найти угол между диагоналями параллелограмма, построенного на векторах a(6;−1;1) и b(2;3;1) .
2.34. Найти угол между векторами a = 3p + 2q |
и b = p +5q , |
где |
p |
и |
q |
– |
||
единичные ортогональные векторы. |
|
|
|
|
|
|
||
2.35. Найти угол между векторами a = p −q и |
b = 2 p + 4q , |
где |
p |
и |
q |
– |
||
единичные векторы, и ( p,q) = |
2π |
. |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
2.36.Найти угол между биссектрисами углов xOy и xOz .
2.37.Из вершины квадрата проведены две прямые, делящие противоположные стороны пополам. Найти угол между этими прямыми.
2.38.Найти угол между биссектрисами двух плоских углов треугольной пирамиды, имеющих общую вершину, если все ребра пирамиды равны.
2.39.Даны точки A(2;−3;4), B(5;−5;−2), C(1;2;3), D(7;4;6) . Найти Пр CD AB .
40
