Частина 2

Основні елементарні функції

Функції y = C (C = const), y = xα (α = const), y = ax (a > 0, a ≠ 1), y =

=logax (a > 0, a ≠ 1), y = sinx, y = cosx, y = tgx, y = ctgx, y = arcsinx, y =

=arccosx, y = arctgx, y = arcctgx називаються основними елементарними

функціями.

Функції, одержані з основних елементарних за допомогою скінченної кількості суперпозицій і арифметичних операцій, називаються

елементарними.

Питання для самоперевірки

1.Сформулюйте означення функції.

2.Сформулюйте означення області визначення функції.

3.Які існують способи задання функції?

4.Яка функція називається парною (непарною)? Які види симетрії вони мають?

5.Яка функція називається періодичною? Наведіть приклади.

6.Яка функція називається монотонною?

7.Яка функція називається обмеженою зверху (знизу), обмеженою?

8.Яка функція називається складною?

9.Назвіть основні елементарні функції.

1.2.ПОСЛІДОВНОСТІ

1.2.1. Числова послідовність. Основні означення

Функцію xn = f(n), задану на множині натуральних чисел N (n N),

називають числовою послідовністю і позначають {xn }={x1, x2 , ..., xn , ...}.

Числа x1, x2, …, xn,… називають членами (елементами) послідовності, xn – загальним (n-м) членом, а n – його номером. Кажуть ще, що змінна x пробігає значення послідовності {xn }.

Загальний член послідовності є функцією від номера n: xn = f(n), n N.

Приклад 1.10. {(–1)nn}={–1, 2, –3, 4, …}.

Обмежені та необмежені послідовності

Послідовність {xn} називається обмеженою зверху (знизу), якщо всі її члени не більші (не менші) деякого числа M: xn ≤ M, (xn ≥ M) (n N).

Послідовність {xn} називається обмеженою, якщо всі її члени за модулем не більші деякого додатного числа M: |xn| ≤ M, (n N, M > 0).

ДВНЗ “Українська академія банківської справи НБУ”

11

Наприклад, якщо ε = 0,1, то N (ε) =[1/ 0,3]+1 = 4 і xn = 1/ 2n < 0,1

при n ≥ 4, для ε = 0,01 маємо N (ε) =[2 / 0,3]+1 = 7 і xn = 1/ 2n < 0,01 при n ≥ 7.

Геометрична ілюстрація означення границі послідовності

Інтервал (а – ε, а + ε) називається ε-околом точки а.

З означення границі випливає, що якщо а – границя {xn}, то для будь-якого ε-околу точки а завжди існує таке N, що члени послідовності з номерами, більшими за N, знаходитимуться усередині ε-околу точки а. Лише скінченна кількість її членів може знаходитися поза цим околом.

1.2.3. Теореми про границі послідовностей

Теорема 1. Якщо границя послідовності існує, то вона єдина

Z Припустимо, що послідовність має дві границі: а і b (а ≠ b). Це означає, що ε > 0 існує таке натуральне число N = N(ε), що для всіх членівпослідовностізномерамиn > N виконуються нерівності: |xn – a| < ε, |xn – b| < ε. Візьмемо ε = (b – a) / 2, тоді ε-околи точок a і b не перетинатимуться. За означенням границі усі члени послідовності з номерами n > N(ε) повинні належати одночасно ε-околам точок a і b, що неможливо. Отже, припущення, що a ≠ b неправильне.

Теореми 2-4. Якщо існують скінченні границі послідовностей

Якщо для послідовностей {xn}, {yn} і {zn} виконуються

ДВНЗ “Українська академія банківської справи НБУ”

13

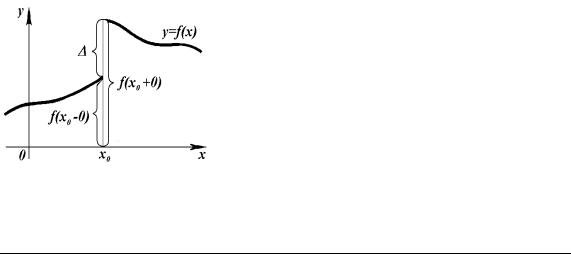
1.3. ГРАНИЦЯ ФУНКЦІЇ

Границя функції на нескінченності

Число А називається границею функції f(x) при х → +∞ (х → −∞),

якщо для довільного малого числа ε > 0, знайдеться таке число Μ, що для всіх х > Μ (х < Μ) виконуватиметься нерівність f(x) − A < ε. Символічно це записують так:

Зауваження. Якщо f(x) → A при х → +∞ (х → −∞), то пряма y = A

є горизонтальною асимптотою графіка функції y = f(x) при х → +∞ (х → −∞).

Границя функції в точці

Нехай функція y = f(x) визначена в деякому околі точки х0 (у самій точці х0 функція f(x) може не існувати).

Число А називається границею функції f(x) у точці х0 (при х → х0),

якщо для довільного малого ε > 0 існує таке число δ(ε) > 0, що для всіх x D(f), які задовольняють умову 0 < х − х0 < δ, виконується не-

рівність f(x) − A < ε. Записують це так: lim f (x) = A, або f(x) → A

x→x0

при х → х0.

Односторонні границі

Означення границі функції в точці х0 було дано незалежно від способу прямування змінної х до точки х0. Якщо х → х0 зліва (х < х0), і при цьому функція f(x) прямує до числа А¯, то число А¯ називають лівосторонньою границею функції та позначають одним із таких способів:

Аналогічно визначається правостороння границя А+ функції у точці х0:

Лівостороння й правостороння границі

називаються односторонніми границями.

Рис. 1.3

ДВНЗ “Українська академія банківської справи НБУ”

15

Нехай lim α(x) = A, тоді:

x→x0 β(x)

1.Якщо A = 0 , то функція α(х) називається нескінченно малою більш високого порядку малості, ніж функція β(х). Символічно це записують так: α(х) = о(β(х)) (читається “о − мале”);

2.Якщо число А≠ 0, А≠1, то α(х) і β(х) – нескінченно малі одного порядку малості. Записують це так: α(х) = О(β (х)) (читається “О – велике”).

3.Якщо lim (α(x)) = A ≠ 0 , то α(х) – нескінченно мала n-го порядку

→x0 β(x) n

малості щодо β(х).

4. Якщо lim α(x) =1, то α(х) і β(х) – еквівалентні нескінченно малі

x→x0 β(х)

функції. Еквівалентність позначається так: α(х) β(х).

Має місце властивість: якщо при х → x0 (х → ∞) f(x) f1(x) і g(x)

g1(x), то

Якщо lim f (x) = 0, тобто f(x) нескінченно мала функція при

x→x0

( x→∞)

x → x0 (x → ∞), то при обчисленні границь зручно користуватися та-

ким рядом еквівалентних нескінченно малих функцій: sinf(x) tgf(x)

arcsinf(x) arctgf(x) ln[1 + f(x)] ef(x) − 1 n (n 1 + f ( x ) − 1) f(x).

1.5. НЕСКІНЧЕННО ВЕЛИКІ ФУНКЦІЇ

Функція f(x) називається нескінченно великою при x → x0 (у точці x0), якщо для будь-якого великого числа М > 0 знайдеться такий δ-окіл точки x0, обумовлений нерівністю 0< x − x0 < δ, для всіх точок якого виконуватиметься нерівність f(x) > Μ. Символічно записують це

так: lim f (x) = ∞ і кажуть, що функція f(x) прямує до нескінченності

x→x0

при х → x0.

Якщо замість нерівності f(x) > Μ виконується нерівність f(x) >

> Μ (f(x) < −M), то записують це так: lim f (x) = +∞ ( lim f (x) = −∞ ).

x→x0 x→x0

Зауваження. Якщо lim f (x) = ∞, то пряма х = x0 є вертикальною

x→x0

асимптотою графіка функції y = f(x) при х → x0.

ДВНЗ “Українська академія банківської справи НБУ”

17

(i =1, 2, ..., n), тоді в околі точки х0 можна подати функції у вигляді:

5) теорема (про границю проміжної функції). Якщо ϕ(x) ≤ f (x) ≤ g(x),

Зауваження. Властивості1-5 виконуютьсяіприx → ±∞, x → x0 ± 0.

1.7.ВИЗНАЧНІ ГРАНИЦІ

1.7.1.Перша визначна границя

ДВНЗ “Українська академія банківської справи НБУ”

19