Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

0887578_645D9_denisyuk_v_p_repeta_v_k_gaeva_k_a_kleshnya_n_o_visha_matemat

.pdf

Скачиваний:

Добавлен:

19.02.2016

Размер:

2.32 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 2815 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

5.8. Інтегрування інтегралів вигляду ∫ R( x, ax2 + bx + c )dx

за допомогою тригонометричних підстановок

За допомогою підстановки x = t − 2ba даний інтеграл зводиться до од-

ного з випадків, поданих у табл. 2.6. Одержані інтеграли за допомогою відповідних замін зводяться до інтегралів вигляду

∫ R(sin z, cos z)dz , або ∫ R(sh z, ch z)dz .

								Таблиця 2.6

№		Інтеграл					Заміна


1	∫ R(t,	t 2	+ m2 )dt	t = m tg z , або t = m ctg z , або t = m sh z
2	∫ R(t,	t 2	− m2 )dt	t =	m	, або t =	m	, або t = m ch z
2	∫ R(t,	t 2	− m2 )dt	t =	cos z	, або t =	sin z	, або t = m ch z
					cos z		sin z

3	∫ R(t,	m2 − t 2 )dt		t = m sin z , t = m cos z , t = m th z

	Т.5		ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Знайдіть інтеграли
1. ∫		dx	.

	1 − x − 2x2

Розв’язання. Запишемо окремо процес виділення повного квадрата:

			2			2		x		1						1	2		1		1			9				1	2
1− x − 2x				= −2	x		+		−				= −2 x		+			−		−		=	2		− x		+			.
1− x − 2x				= −2	x		+	2	−	2			= −2 x		+	4		−	16	−	2	=	2		− x		+	4		.
								2		2						4			16		2		16					4
Тоді
Тоді
∫				dx		= ∫							dx				= 1			∫		d(x + 1/ 4)							=
∫						= ∫									2		= 1			∫									=
	1	− x − 2x2										9		1	2				2			3	2			1	2
									2				− x +										− x +
									2		16		− x +	4								4	− x +			4
											16			4								4				4

141

		=	1	arcsin	x + 1/ 4	=	1	arcsin	4x + 1	+ C .
			2		3 / 4		2		3
2. ∫	(x − 2)dx			.
2. ∫	4x	2 + 4x	+ 17	.
	4x	2 + 4x	+ 17

Розв’язання. Виділимо у чисельнику підінтегральної функції похідну від знаменника. Оскільки (4x 2 + 4x + 17)′ = 8x + 4 , то запишемо чисельник підінтегральної функції так:

x − 2 =

(8x + 4) −

− 2 =

(8x +4) −

(4x2 +4x +17)

′−

Тоді

∫

(x − 2)dx

= ∫

(

(8x + 4) −

)dx

∫ d(4x 2 + 4x + 17) −

4x 2 + 4x + 17

−

5 ∫

4x 2 + 4x + 17 −

∫

d(2x + 1)

+ 4x + 17

(2x + 1)

+ 16

4x 2 + 4x + 17 −

5 ln 2x + 1+ 4x 2

+ 4x + 17 + C.

Тут

ми

скористалися

табличними інтегралами

∫ du

u + C та

2 u

∫

= ln

u + u2 ±a2

+C .

u2 ±a2

3. ∫

dx .

x + 3

x 2

Розв’язання. Найменше спільне кратне чисел два та три дорівнює числу шість, тому виконаємо заміну x = t 6 , dx = 6t 5 dt . Тоді

∫	3 x	dx = ∫		t 2		6t 5 dt
	x + 3 x 2		t	3	4
				+ t

= 6∫ (t 2 + 1)(t − 1)(t + 1) + 1dt = t + 1

	6∫	t 4		dt = 6∫	(t 4	− 1) + 1
=									dt		=
		t +				t + 1
			1
6∫ (t 2 + 1)(t − 1)dt +						6∫		dt		=
							t	+ 1

142

= 6∫ (t 3 − t 2 + t −1)dt + 6∫

t 4 − 2t 3 + 3t 2 − 6t + 6 ln

t + 1

+ C =

+ 1

3 x 2 − 2 x + 3 3

x − 6 6 x + 6 ln 6 x + 1 + C .

4. ∫

3 2 − x dx .

− x)

2 + x

Розв’язання. Застосуємо заміну

2 − x

= t3. Звідси

2 + x

x =

2 − 2t

, 2 − x =

4t 3

, dx = −

12t 2 dt

1+ t

1+ t 3

(1+ t

3 )2

Отже,

12t2

∫

2 − x

∫

1+ t

3 dt

dx = −

dt =

−

∫

(2 − x)

2 + x

(1+ t

)

+ C =

+ x 2

+ C .

− x

5. ∫

x 2

1+ x

dx .

+ x

Розв’язання. Тут дробово-лінійна функція

ax + b

звелась просто до лі-

cx + d

нійної функції 1+ x . Покладемо 1+ x = t 4 , тоді x = t 4 − 1 , dx = 4t 3 dt .

Отже,

∫

x 2 + 1+ x

dx = ∫

(t 4

− 1) 2 + t 2

dt =

4∫((t

− 1)

+ t

4 1+ x

= 4∫ (t10 − 2t 6 + t 2 + t 4 )dt =

t11

−

7 +

t 3

t 5

+ C =

4 4

(1+ x)11 −

8 4

(1+ x)7 +

4 4

(1+ x)3 +

4 4

(1+ x)5 + C .

6. ∫

4 (x − 1)

3 (x + 2)5

143

Розв’язання. Оскільки

4 (x − 1)3 (x + 2)5

= (x − 1)(x + 2) 4

x + 2

, то під-

x − 1

інтегральний вираз — раціональна функція від x та 4

x + 2

. Тому викону-

x − 1

x + 2

ємо підстановку

= t4 . Звідси

x − 1

3t4

12t3dt

x =

+ 2

, x − 1

, x + 2 =

dx = −

− 1

t4 − 1

t4 −

(t4 − 1)2

Тоді

∫

= ∫

4 (x −1)3 (x + 2)5

x + 2

(x − 1)(x + 2) 4

x − 1

t 4

− 1

t 4

− 1

− 12t 3

x −

= ∫

dt = −

∫

+ C =

+ C .

− 1)

x +

Інтегрування диференціальних біномів

7. ∫ x (3 − 3 x )2 dx .

Розв’язання. Маємо найпростіший випадок, структура підінтегрального виразу дає можливість провести інтегрування без заміни:

					1					1				2										1				5	7
∫ x (3 − 3 x )2 dx = ∫ x								(9 − 6x							+ x				) dx = ∫(9x								− 6x		+ x		) dx =

						2							3				3									2		6		6
							3				36			11				6			13
																+
					= 6x		2		−			x			6	+					x 6 + C .
										11				13
8. ∫	3 4 x − 1dx .
	x
Розв’язання. Запишемо даний інтеграл у вигляді
					3 4 x − 1dx =									1							1			1
				∫										∫ x −
				∫										∫ x −			2		(x			4	− 1) 3 dx .
					x
Тут	p =	1	, m = −	1	, n =				1	. Оскільки										m + 1				=	−1/ 2 + 1				= 2 — ціле чис-
		3		2					4													n			1/ 4

ло, то маємо другий випадок (табл. 2.4). Виконаємо заміну x4 − 1 = t3 , бо знаменник p дорівнює 3. Далі маємо

144

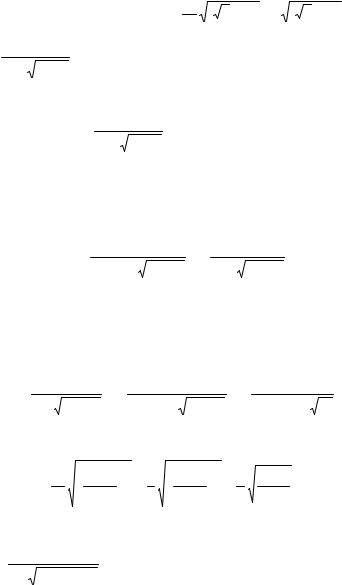
x = (t 3 + 1) 4 , dx = 12(t 3 + 1)3 t 2 dt ,

∫ x −

= ∫ (t 3 + 1) 4(−

) (t 3 )

12(t 3 + 1)3 t 2 dt =

− 1)

=12∫ (t

+ 3t

+ C

12 3

x − 1)

+ C .

+1)t

= 7

(

+ 3 (

9. ∫

x11

1+ x 4

Розв’язання. Запишемо інтеграл у вигляді

I = ∫

= ∫ x −11 (1+ x 4 ) −

dx .

x11 1+ x 4

Тут p = −

m = −11,

n = 4 . Оскільки

m + 1

+ p

= −3 — ціле число, то

маємо третій випадок з табл. 2.4. Інтегрування починаємо з винесення множника x 4 з-під знака кореня:

= ∫

∫

x11 x 2 x −4 + 1

x13 x −4 + 1

Виконаємо

заміну

x −4 + 1 = t 2 ,

−4x−5dx = 2tdt,

звідси

x −4 = t 2 − 1,

x −5 dx = −

tdt . Чисельник і знаменник під знаком інтеграла множимо на

x −5 , дістаємо

x −5 dx

−

tdt

I = ∫

= ∫

x8 x −4 + 1

(x −4 )−2 x −4 + 1

(t 2 − 1) −2 t 2

= −

∫ (t 2

− 1) 2 dt = −

∫ (t 4

− 2t 2

+ 1)dt =

−

t 5

t 3 −

t + C =

= −

+ x

+ x 4 3

−

1 1

+ x

+ C .

Підстановки Ейлера

10. ∫

+ x

2 + 2x + 2

145

(1− t)t 2

Розв’язання. Тут a = 1 > 0 , застосуємо підстановку

x 2 + 2x + 2 = t + x .

Тоді

x 2 + 2x + 2 = t 2 + 2tx + x 2 , 2x + 2 = t 2 + 2tx , x =

t 2 − 2

2(1− t)

dx =

− t 2 + 2t − 2

dt , 1+ x

+ 2x + 2

= 1+ t +

t 2 − 2

= −

2(1

− t)2

2(1− t)

2(1

− t)

Після цього приходимо до інтеграла

∫

= ∫

(−t 2 + 2t − 2)

2(1− t)

dt =

1+ x

2 + 2x + 2

2(1

− t)

(−t

)

= ∫ t 2 − 2t + 2dt .

Розкладемо тепер підінтегральну функцію на елементарні дроби:

t2 − 2t + 2

t2 + 2(1− t)

(1− t)t2

− t

Отже,

∫

t 2 − 2t + 2

dt = 2∫

+ ∫

= −

− ln

t − 1

+ C .

(1− t)t

1− t

Повертаючись до змінної x , дістаємо відповідь

∫

− ln1+ x − x 2 + 2x + 2 + C .

1+ x 2 + 2x + 2

x − x 2 + 2x + 2

11.

I = ∫

(x + 1) x 2 + 4x + 2

Розв’язання. Покладемо x + 1 =

, dx = −

, дістанемо

t 2

146

I = −∫

dt2 = − ∫

− 1

+ 2

2 +

− 1

= −∫

= − arcsin t −1 + C =

+ 2t − t2

2 − (t −1)2

− 1

= − arcsin

x + 1

+ C = arcsin

+ C .

2(x + 1)

Метод М. Остроградського

12. I = ∫

x 2 dx

x 2 + x + 1

Розв’язання. В чисельнику стоїть многочлен другого степеня, тому

∫

x 2 dx

= (Ax + B) x 2 + x + 1 +λ∫

x2 + x + 1

x 2 + x + 1

Продиференціюємо обидві частини рівності за змінною x :

(Ax + B)(2x + 1)

= A

+ x + 1

x 2 + x + 1

2 x 2 + x + 1

x2 + x + 1

звідси після зведення до спільного знаменника дістаємо

2x 2

= 2A(x 2 + x + 1) + (Ax + B)(2x + 1) + 2λ .

Застосовуючи метод порівняння коефіцієнтів, дістаємо

x 2 : 4A = 2,

A =

;

x : 3A + 2B = 0,

B = −

;

x0 : 2A + B + 2λ = 0,

λ = −

Отже,

∫

x 2 dx

x −

+ x

+ 1 −

∫

x 2 + x

+ 1

2 + x + 1

де ∫

= ∫

d(x + 1/ 2)

= ln x + 1/ 2 + x 2 + x + 1 + C .

x 2 + x + 1

(x + 1/ 2)2 + 3 / 4

147

Зауваження. Інтеграл

∫ R(x,

ax 2 + bx + c )dx = ∫

− α )n

ax 2 + bx + c

заміною

= t

зводиться до інтеграла ∫

(t)dt

x − α

+ bt + c

13.

I = ∫

+ 2)

3 x 2 + 4x

Розв’язання. Виконаємо заміну

+ 2 =

dx = −

. Тоді

t 2

−

t2dt

∫

= ∫

=∫

= −∫

(x + 2)3 x2 + 4x

(x + 2)3 (x + 2)2 − 4

− 4

1− 4t2

Згідно з методом Остроградського маємо

∫

t 2 dt

= ( At + B) 1− 4t 2 +λ ∫

1− 4t 2

1− 4t2

Звідси після диференціювання дістанемо

= A 1− 4t 2

−

( At + B) 4t

або

1− 4t 2

t 2 = A(1− 4t 2 ) − 4t( At + B) + λ .

Прирівнявши коефіцієнти при однакових степенях t , знайдемо

A = −

B = 0 ,

λ =

Отже,

∫

t 2 dt

= −

1 t

1− 4t 2 +

arcsin 2t + C .

1− 4t

148

Повертаючись до змінної x , остаточно дістаємо

I = −

1−

arcsin

+ C =

8(x + 2)

(x + 2)2

x + 2

+ 4x

arcsin

+ C.

8(x + 2)2

x + 2

Інтегрування ірраціональних функцій за допомогою тригонометричних підстановок

14. I = ∫	3 − 2x − x 2
	(x + 1)	2	dx .

Розв’язання. Виділимо повний квадрат підкореневого виразу: 3 − 2x − x2 = = 4 − (x + 1)2 . Тепер зрозуміло, що можна виконати підстановку x + 1 = 2sin t, dx = 2 cos tdt . Тоді

I = ∫

4 − (x + 1)

= ∫

4 − 4 sin 2 t

2 cos tdt = ∫

2 cos t

2 cos tdt =

4 sin

= ∫

cos 2 t

dt =

∫

1− sin 2 t

∫

−∫ dt =−ctg t −t +C .

sin

Щоб перейти до змінної x , зауважимо, що sin t =

x + 1

. Звідси

1− sin 2

−

+ 1) 2

3 − 2x − x 2

t = arcsin

x + 1

ctg t

cos t

sin t

x + 1

Остаточно дістаємо

I = −

3 − 2x − x

− arcsin

x + 1

+ C .

x + 1

15. I = ∫

+ 25dx

Розв’язання. Зробимо заміну x = 5 tg t , тоді

149

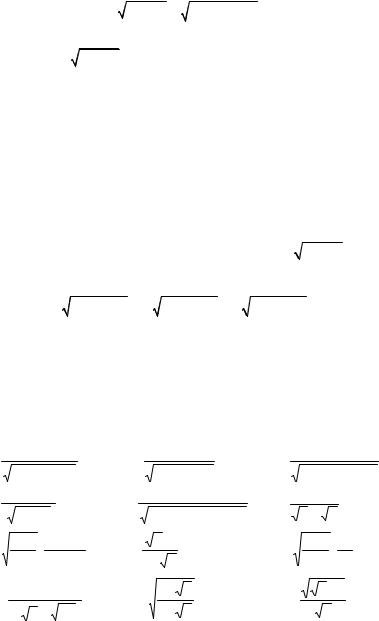
dx =

5dt

, x2 + 25 = (5 tg t)2 + 25 =

cos2

cos t

5dt

x2 + 25dx

cos5 tdt

I = ∫

=∫

cos t

cos2 t

=25∫

sin

(1− sin2 t)2 d sin t

= 25∫

=25∫

−

d sin t

sin

+ C .

= 25

−

7 sin

5sin

3sin

Повернемося до змінної x :

tg t =

;

+ 25

sin t =

sin2 t

sin

x2 + 25

Отже,

25)

+ 25)

I = 25

−

+ C.

7x7

Т.5

ВПРАВИ ДЛЯ АУДИТОРНОЇ

І САМОСТІЙНОЇ РОБОТИ

Знайдіть інтеграли.

1. ∫

2. ∫

3. ∫

(3x − 5)dx

x 2 + 6x + 11

3 + 2x − x 2

2x 2 − 12x + 15

∫

(6x + 1)dx

5. ∫

(2 sin x − 1) cos xdx

6. ∫

x − x 2

5 + 4 sin x − sin 2 x

x +

∫

3 x + 1

3 .

∫

6 xdx3 .

∫

x − 3

dx .

x − 1

(x − 1)

1+ x

10. ∫

11.

∫

1−

x dx .

12. ∫

3 4 x + 1dx .

x( x + 5 x 2 )

1+ x

150

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 2815 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.04.20196.01 Mб39(Т3укр)м(Л14).doc
#
29.08.20195.47 Mб21(Т4 укр)м(Л21).doc
#
29.08.20193.68 Mб36(Т5укр)м(Л22-23).doc
#
11.12.2018296.96 Кб12+Изгот микросхем.doc
#
11.12.2018437.76 Кб3+страничная память.doc
#
19.02.20162.32 Mб210887578_645D9_denisyuk_v_p_repeta_v_k_gaeva_k_a_kleshnya_n_o_visha_matemat.pdf
#
19.02.20163.59 Mб510887579_C36AB_denisyuk_v_p_repeta_v_k_gaeva_k_a_kleshnya_n_o_visha_matemat.pdf
#
19.09.2019106.5 Кб01 000 000 $.doc
#
16.11.20191.38 Mб11 Lab (Neuro).docx
#
19.02.20161.12 Mб1001 Конспект лекций Основы системного анализа.doc
#
25.11.2019238.27 Кб41 Літосферні стихійні лиха.docx