Учебник логики

а принадлежит мн-ву В

мн-во В содержит а

а находится в отношении принадлежности к мн-ву B

В математике и логике стремятся использовать такие способы записи, чтобы они были, по возможности, краткими и ясными. Вместо того, чтобы говорить, что «предмет а является элементом мн-ва В», используют значок или , которые называются знаками принадлежности, и записывают это в виде

а В.

Обозначим мн-во всех натуральных чисел посредством N. Как записать, что число 0 и число 1 принадлежат ему? Сделать это очень просто.

0 N и 1 N.

Если мы хотим записать, что некоторый предмет а не принадлежит мн-ву В, мы просто перечеркиваем знак принадлежности а В.

Часто для облегчения восприятия пользуются графическим изображением множеств и элементов. Это так называемые круги Эйлера и диаграммы Венна.

В первом случае, чтобы изобразить множество, мы рисуем круг, а элементы помещаем внутри него. Как изобразить то, что элемент не принадлежит множеству? Очень просто. Мы рисуем круг, изображающий множество, а элемент, о котором идет речь, рисуем вне этого множества.

71

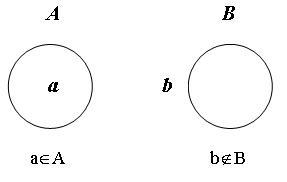
Рис. 3-1

Вопрос. Какие виды знаков из классификации Пирса присутствуют на это рисунке?

Часто во время рассуждения необходимо фиксировать всю предметную область, совокупность предметов, о которых будет идти речь. Эту совокупность предметов называют универсумом рассуждения. В этих случаях для изображения отношений между множествами пользуются диаграммами Венна.

Универсум рассуждения изображают в виде прямоугольника, а множества, являющиеся его частями, изображают в виде кругов внутри него или частей. Например, мы можем изобразить всех мыслимых животных в виде прямоугольника, а стадо коров и стадо овец нарисовать в виде кругов внутри этого прямоугольника. Когда нет необходимости говорить обо всех мыслимых предметах (универсуме рассуждения), обходятся кругами Эйлера.

72

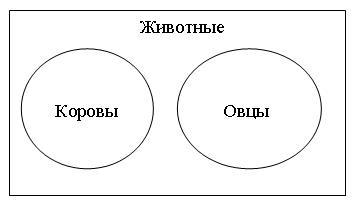
Рис. 3-2

3.3 Способы задания множеств

Каким образом, посредством каких мыслительных операций можно образовывать множества?

Первый способ - просто перечислить предметы, которые входят в конкретное мн-во. Например, можно по фамилиям и именам перечислить студентов, находящихся в данный момент в данной аудитории. Множество четных чисел меньше десяти можно задать путем их перечисления - 0, 2, 4, 6, 8. Чтобы отразить мысль, что эти числа составляют именно множество, их помещают в фигурные скобки и записывают в виде {2, 4, 6, 8}. Данный способ задания множеств прост, но удобен лишь в тех случаях, когда совокупность элементов не слишком велика и каждый из них может быть поименован.

Второй способ - задать множество посредством некоторой процедуры, или правила, порождающего элементы, входящие в это множество. Это удобно в тех случаях, когда мы не можем явным образом перечислить все элементы. Множество всех натуральных чисел меньше миллиона можно перечислить, но

73

запись будет слишком громоздкой. Гораздо проще задать его следующим образом с помощью правила

{0, 1, 2,…n, n+1,…, 999999}

Смысл его достаточно прозрачен. Мы задаем начальные элементы множества, затем записываем правило порождения последующих элементов, и в конце записываем последний элемент, к которому правило уже не применяется.

В случае задания бесконечного множества всех натуральных чисел простой пересчет вообще невозможен, и нам не остается ничего другого, как задать его с помощью правила.

{0, 1, 2,…n, n+1,…}.

Вопрос.

1.Как задать множество всех четных чисел?

2.Как задать множество всех нечетных чисел?

3.Как задать множество всех натуральных чисел, являющихся квадратами?

Третий способ - задание множеств путем указания свойств, признаков, которыми обладают его элементы и только они. Вспомним учение Аристотеля о том, что формы (свойства) существуют не сами по себе, а посредством вещей, которые ими обладают. Это означает, что каждому свойству можно сопоставить совокупность вещей, являющихся его носителями. Именно эта идея и лежит в основе третьего способа задания множеств. Для этого используют следующую запись, которая читается как «множество предметов, обладающих свойством P».

{x | x обладает свойством P}.

74

Например, множество {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} мы могли бы задать путем указания на то, что его элементами являются натуральные числа меньше 10. Конкретные варианты записи могут слегка отличаться

{x | x-натуральное число меньше 10}

или

{x | x-натуральное число и x 10}

или

{x | x N и x 10}

Вопрос

1.Как установить, что некоторые предмет a принадлежит множеству {x| x обладает свойством P}?

2.Как задать множество {2, 4, 6, 8} путем указания свойства, которыми обладают его элементы?

Четвертый способ - задание множеств посредством некоторых операций над уже имеющимися множествами, которые были созданы ранее.

Например, фермер владеет двумя стадами животных - стадом коров и стадом овец. Два стада - это два четко определенных множества, заданных посредством перечисления их элементов. Из этих двух множеств мы можем образовать новое множество всех животных, которыми владеет фермер. Для этого нам не нужно заново перечислять их, а достаточно мысленно объединить вместе множество коров и множество овец, которые нам уже известны. Операция объединения множеств позволяет из двух множеств создать третье множество, которое будет состоять из элементов двух исходных множеств. Кроме объединения, есть и другие операции.

Аналогичным образом из двух множество {1, 3, 6} и {2, 3, 4, 5} посредством операции объединения мы можем получить новое множество {1, 2, 3, 4, 5, 6}.

75

3.4 Множества как элементы других множеств

Еще раз напомним, что Кантор понимал множество как

любое собрание определенных и различимых между собой объектов нашей интуиции или интеллекта, мыслимое как единое целое.

Множество овец, принадлежащих конкретному фермеру, четко определено, и столь же четко определено множество принадлежащих ему коров, которое отлично от множества овец. Мы имеем полное право (а почему бы и нет?) составить из двух этих множеств новое двухэлементное множеств стад животных, принадлежащих нашему фермеру.

Стадо_овец = {a, b, c} Стадо_коров = {k,l,m,n}

Мн-во_стад_животных = {Стадо_овец, Стадо_коров} = {{a, b, c}, {k,l,m,n}}

Вопрос.Какие примеры множеств, элементами которых в свою очередь являются множества, вы можете привести?

Является ли множеством {Кремль, число , человеческие_эмоции}? Перечисленные объекты определены? Да. Перечисленные объекты различимы между собой? Да. Почему бы тогда не помыслить их как единое целое? В подтверждение этому мы даже привели запись даннного множества. Как бы нас ни шокировало объединение в одно множество столь разнородных объектов, но оно удовлетворяет нашему пониманию множеств и потому может считаться таковым.

3.5 Пустое множество

76

Рассмотрим множество {x| x - человек, и x побывал на Марсе}. Поскольку в настоящий момент еще ни один человек не побывал на Марсе, то это множество не содержит ни одного элемента, оно - пустое. Так и будем его называть. Можно провести аналогию между пустым множеством и нулем в арифметике. В теории множество его специально выделяют и обозначают символом . Коль скоро оно пусто, не содержит ни одного элемента, то для него справедливо следующее утверждение.

Для всякого предмета x верно, что x .

Другие примеры пустых множеств.

{x| x- натуральное число, и x 5, и x 10}

{x| x - вечный двигатель}

{x| x - квадрат, x - не квадрат}

Как возникают пустые множества? В случае с людьми, побывавшими на Марсе, это множество пусто в силу фактического состояния дел. Можно надеяться, что в ближайшем будущем оно перестанет быть пустым. Множество натуральных чисел, которые одновременно меньше 5 и больше 10 пусто в силу законов арифметики и таким всегда останется. Множество вечных двигателей является пустым в силу законов физики, хотя не перевелись еще энтузиасты, которые каждый год пытаются доказать, что оно не пусто. В последнем примере с геометрической фигурой, которая одновременно является и не является квадратом, множество пусто по причине логической противоречивости свойства, которым оно задано.

Вопрос. Какие еще примеры пустых множеств вы можете привести?

3.6 Равенство множеств

77

В каком случае мы можем сказать, что два множества A и B равны? Ответ напрашивается сам собой. Два множества A и B равны, если они состоят из одних и тех же элементов.

Множество A равно множеству B, если и только если каждый элемент множества А является элементом множества В, а каждый элемент множества В, является элементом множества А

или

A = B, если и только если для всякого предмета x верно, что если x A, то x B, и если x B, то x A.

Можно проверить, что отношение равенства между множествами обладает следующими свойствами.

1.A=A

2.Если A=B, то B=A

3.Если A=B и B=C, то A=C

Этими же свойствами обладает отношение равенства чисел в арифметике.

Сделаем маленькое отступление, чтобы сказать несколько слов о том, как понимается равенство в логике. Насколько осмысленно утверждение, что два объекта a и b равны? Если это действительно два объекта, то они должны чем-то отличаться друг от друга. Именно это и дает нам основание говорить о том, что их два. Следовательно, утверждение, что они равны, никогда не может быть верным. Правильным было бы сказать, что два выражения языка «a» и «b» обозначают один и тот же объект. Обнаружение данного факта зачастую имеет познавательную ценность. Например, из энциклопедии вы можете узнать, что

самая высокая гора на Земле = Эверест. Речь идет не о двух объектах, а об одной и той же горе, обозначенной двумя разными

78

выражениями языка. Так же можно узнать, что

Эверест = Джомолунгма.

В случае теории множеств мы можем быть заинтересованы в обнаружении того, что два разных способа задания множества приводят к одному и тому же результату - одному и тому же обозначаемому ими множеству.

Вопрос

1.Равны ли множества {x| x=1 или x=3 или x=5} и {x| x - нечетное число меньше 6}?

2.Равны ли множества {x| x - вечный двигатель} и {x| x - человек, побывавший на Марсе}?

3.Если нужно доказать, что два множества {x| x обладает свойством A} и {x| x обладает свойством B} равны, то как это сделать?

3.7Включение множеств

Рассмотрим два множества {1, 3, 5, 7, 9} и {x| x - число меньше 10}. Очевидно, что эти множества не равны. В то же время каждый элемент первого множества одновременно является элементом второго. Это пример отношения включения между множествами.

Множество А включено в множество В, е. и т.е. каждый элемент множества А является элементом множества В.

Кроме выражения «A включено в B» используют также выражение «множество A является подмножеством множества B» Обозначают отношение включения посредством символа . С его помощью мы можем записать определение отношения включения между множествами более кратко.

79

A B е. и т.е. для всякого предмета x верно, что если x A, то x B.

Вопрос. Если два множества A и B равны, то какие из

следующих утверждений будут истинными, а какие ложными?

1. А В

2. А=В

3. А В

4. В А

Вопрос. Если A B и В А, то что можно сказать об утверждении А=В?

Вопрос. Какие из следующих утверждений верны, а какие - нет?

1.A A

2.Если A B, то В А

3.Если A B и B C, то A C

4.Если A C и B C, то A=B

5.Если C A и C B, то A=B

6.Если A B и B C, то C A

Вопрос. Пусть В - произвольное множество. Какие

утверждения верны, а какие нет?

1. B

2. B

С помощью кругов Эйлера отношение включения между множествами A и B может быть изображено одним из следующих двух способов. Во втором случае эти множества просто равны.

80