Учебник логики

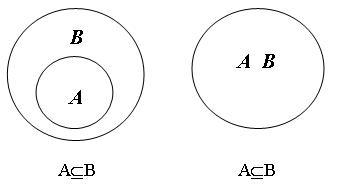
Рис. 3-3

3.8 Операции объединения, пересечения, разности и произведения множеств

Четвертый способ образования множеств предполагает использование операций над ними.

Объединение множеств

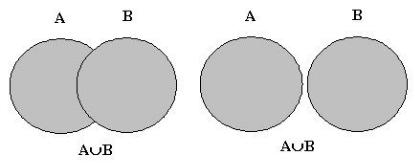
Если даны два множества А и В, то мы можем построить третье множество путем объединения двух первых. Результат объединения обозначают посредством A B. Он состоит из тех элементов, которые принадлежат исходным множествам.

x A B е. и т.е. x A или x B

Это же определение можно записать несколько иначе

A B = {x| x A или x B}

Примеры:

{1,2,3} {2,3,4,5} = {1,2,3,4,5}

{1,2,3} = {1,2,3}

81

Свойства

A А= A

A B= В А

(A B) С = А (В С)

A = A

Вопрос. Какие из свойств объединения двух множеств аналогичны свойствам сложения чисел в арифметике, а какие нет?

На кругах Эйлера объединение двух множеств A и B представляют следующим образом.

Рис. 3-4

Закрашенные области - это результат операции объединения.

Пересечение множеств

Если даны два множества А и В, то мы можем построить третье множество путем пересечения двух первых. Результат пересечения обозначают посредством A B. Он состоит из тех элементов, которые одновременно принадлежат обоим исходным множествам.

82

x A B е. и т.е. x A и x B

Это же определение можно записать несколько иначе

A B = {x| x A и x B}

Примеры:

{1,2,3} {2,3,4,5} = {2,3}

{1,2,3} =

Свойства:

A А= A

A B= В А

(A B) С = А (В С)

A =

A (B С) =( А В) (A С)

A (B С) =( А В) (A С)

Вопрос. Какие из свойств пересечения двух множеств аналогичны свойствам умножения чисел в арифметике, а какие нет?

На кругах Эйлера пересечение двух множеств можно представить следующим образом.

83

Рис. 3-5

Разность множеств

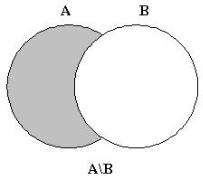
Разностью между множествами А и В называется множество, состоящее из тех элементов А, которые не являются элементами В. Результат операции обозначают посредством A\B.

x A\B е. и т.е. x A и x B

Это же определение можно записать несколько иначе

A\B = {x| x A и x B}

Примеры:

{1,2,3}\{2,3,4,5} = {1}

{2,3,4,5}\{1,2,3} = {4,5}

{1,2,3}\ ={1,2,3}

\{1,2,3}=

Свойства:

A\А=

A\ = A

84

\A=

Вопрос. Какие из свойств разности двух множеств аналогичны свойствам вычитания чисел в арифметике, а какие нет?

На кругах Эйлера разность двух множеств можно представить следующим образом.

Рис. 3-6

Втех случаях, когда фиксирован универсум рассуждения U,

идля изображения отношений между множествами используются диаграммы Венна, разность между универсумом U и множеством A называют дополнением A относительно универсума U, или просто дополнением и обозначают результат как U\A, или просто -A.

Например, в качестве универсума U мы можем взять множество всех птиц, а в качестве множества A - множество всех ворон. Тогда дополнением -A будет множество всех птиц, не являющихся воронами. На диаграмме Венна это можно изобразить следующим образом.

85

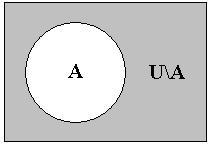
Рис. 3-7

Можно проверить, что имеют место следующие соотношения:

A -A =

A -A = U

--A = A

-(A B) = -A -B

-(A B) = -A -B

Если A B, то -B -A

Произведение множеств

Элементами множеств могут быть не только отдельные предметы и множества, но также пары, тройки и даже произвольные упорядоченные наборы объектов. Произведением двух множеств А и В называется множество, состоящее из всех пар элементов А и В. Результат операции обозначают посредством A B.

<x,y> A B е. и т.е. x A и y B

Это же определение можно записать несколько иначе

86

A B = {<x,y>| x A и y B}

Сами по себе полные произведения множеств особого интереса не представляют. Они нужны нам для того, чтобы выделять в них полезные подмножества.

Например, мы можем образовать произведение множества всех мужчин и множества всех женщин.

MW = Мужчины Женщины = {<x,y>| x Мужчины и у Женщины}

После этого, мы следующим образом выделяем в нем подмножество супружеских пар:

Супруги = {<x,y>| x женат на y, и <x,y> MW}

Заметим, что ничего сложного или необычного в этом определении нет. Именно так мы и понимаем совокупность всех супружеских пар.

Примеры:

{1,2 } {2,3,4} = {<1,2>, <1,3>, <1,4>, <2,2>, <2,3>, <2,4>}

{2,3,4} {1,2} = {<2,1>, <2,2>, <3,1>, <3,2>, <4,1>, <4,2>}

{1,2} =

Свойства:

A =

A =

Вопрос. Какие из свойств разности двух множеств аналогичны свойствам вычитания чисел в арифметике, а какие - нет?

Вопрос. Как определить множество всех пар натуральных чисел, первое из которых меньше второго?

87

3.9 Мощность множеств

Рассмотрим два множества {a, b, c} и {d, e, f}, где все элементы a, b, c, d, e, f попарно не равны друг другу. Очевидно, что эти множества не равны, так как состоят из разных элементов. В то же время каждое из этих множество содержит по три элемента, т.е. они равны по величине. Как, не обращаясь к подсчету числа элементов множеств, определить, равны они по величине или не равны?

Один из способов ответа на этот вопрос - установление

взаимно-однозначного соответствия между элементами двух множеств. Для нашего примера это будет выглядеть следующим образом:

a d b e c f

Каждый элемент первого множества связан с одним элементов второго множества, и наоборот.

Величину множества A называют его кардинальным числом и обозначают, заключая знак множества в прямые скобки |A|.

Два мн-ва A и B равномощны (равны по величине, имеют одинаковый кардинал |A| = |B|), если между их элементами можно установить взаимно-однозначное соответствие.

Очевидно, что из равенства двух множеств следует равенство их кардиналов.

Если A=B, то |A|=|B|

Обратное утверждение в общем случае неверно. Мы убедились на примере, что |{a,b,c}|=|{d,e,f}|, но {a,b,c} {d,e,f}.

88

Рассмотрим другую пару множеств A={a, b, c} и B={d, e, f, g}. Эти множества не равны между собой и не равны по величине. Как бы мы ни старались, но у нас не получится установить взаимно-однозначное соответствие между их элементами. В то же время для нас очевидно, что число элементов множества B больше числа элементов A.

Опять попробуем установить взаимно-однозначное соответствие.

a d b e

cf

?g

Как бы мы ни старались, всегда будет оставаться один элемент множества В, которому не будет сопоставлен ни один элемент А. Каждая попытка найти такое соответствие будет приводить к построению взаимно-однозначного соответствия между элементами множества А и некоторого подмножества множества В, которое не совпадает со всем множеством B.

Множество А меньше по величине (имеет меньшую мощность), чем множество В, если мы можем установить взаимно-однозначное соответствие между элементами множества А и элементами некоторого подмножества В, но не можем сделать это для всего множества В.

В этом случае пишут - |A|<|B|

3.10 Бесконечные множества

Что такое бесконечность? Этот вопрос всегда волновал не только философов, но и простых людей. В рамках теории

89

множеств было дано строгое определение того, что такое бесконечное множество. В непосредственном опыте мы не сталкиваемся с такими множествами, они существуют лишь как мыслимые конструкты.

Примеры:

множество всех натуральных чисел {0, 1, 2,…, n, n+1,…};

множество четных чисел {0, 2,…, n, n+2,…};

множество точек на прямой;

множество точек на плоскости.

Почему мы считаем эти множества бесконечными? В случае натуральных чисел ответ кажется интуитивно очевидным: согласно правилу порождения чисел, для каждого числа существует число, которое больше его на единицу. Поэтому самого большого последнего числа не существует. А как быть с точками на прямой? В этом случае никакой процедуры нет, но мы интуитивно уверены, что они составляют бесконечное множество.

Как определить понятие бесконечного множества независимо от того, каким способом оно задано? Хитроумное решение было найдено. Чтобы лучше оценить его, сделаем небольшое отступление и рассмотрим вариант так называемого «Парадокса Галлилея».

Пусть у нас есть множество всех натуральных чисел {0, 1, 2, …, n, n+1,…} и множество четных чисел {0, 2,…, n, n+2,…}. Мы можем установить взаимно-однозначное соответствие между их элементами с помощью правила: n n 2.

0 0

1 2

2 4

3 6

.

.

90