4.2. Проверка случайности колебаний уровня остаточной последовательности.

Методы: 1) серии, основанные на медиане выбора;

_

i=yi+yii= теоритические остатки;

0,5;-0,5;-1,5;2;-2,3;-0,6

Этапы: 1) упорядоч. порядки по возрастанию -1,5;-0,6;-0,5;2;2,3;

2)срединные значения этого ряда 0,5

3)медиану сравниваем с фактическим: «+» - > медианы₀«-» - меньше медианы₀ 0;-;+;+;-;_ф=3(серии)

Серии К_мф=2

При 5% значимости нулевой гипотезы проверяется как отношение К_мф<[3,3 *log(n+1)]

n-число наблюденийф>[1/2(n+1-1.96)]

Если выполн. 2. неравенство, то выборка считается случайной более 95%. И нулевая гипотеза отвергается. Выборка получается неслучайной.

4.3 Проверка соответствия распределения случайной компоненты нормальному закону распределения

Данная проверка производится обычно приближенно с помощью нахождения показателей ассиметрии γ₁ и эксцесса γ₂. Это производится на основании сравнения найденных показателей с теоретическими. При нормальном распределении некоторой генеральной совокупности показатели ассиметрии и эксцесса должны быть равны нулю (γ₁=0, γ₂ =0). При конечной выборке из генеральной совокупности показатели ассиметрии и эксцесса имеют отклонения от нуля.

Для оценки соответствия выбранной совокупности данных нормальному закону распределения используется так называемая оценка показателей эксцесса и ассиметрии.

В качестве оценки асимметрии используется формула:

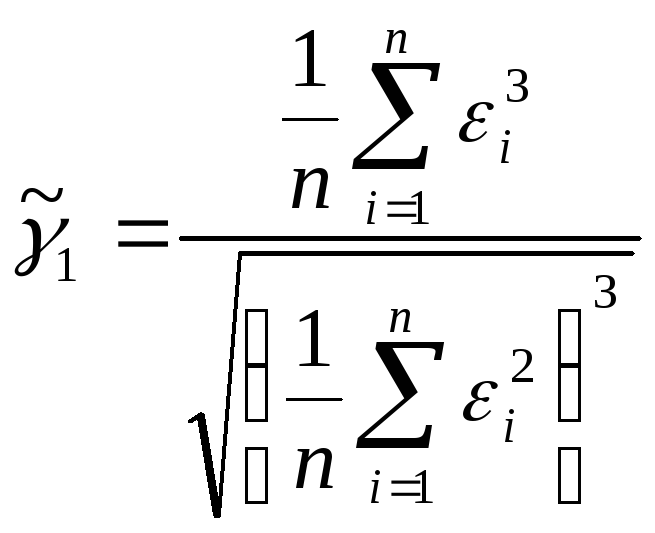
Оценка эксцесса:

Здесь и- соответственно выборочные характеристики ассиметрии иэксцесса, а и- их допустимые среднеквадратичные ошибки,ε_i - остаточная компонента.

Если одновременно выполняются неравенства для 5% уровня значимости 0^ой гипотезы:

то считается, что фактическая кривая распределения допустимо близка к кривой нормального распределения.

Если:

то с вероятностью более 5% можно утверждать, что фактическая кривая распределения недопустимо отклоняется от кривой нормального распределения.

Следовательно, адекватности нет.

Другие случаи требуют дополнительной проверки при помощи более сложных критериев.

4.4 Проверка равенства математического ожидания случайной компоненты нулю.

Проверка равенства математического ожидания случайной компоненты нулю осуществляется на основе t-критерия Стьюдента. Расчетное значение этого критерия находится по формуле:

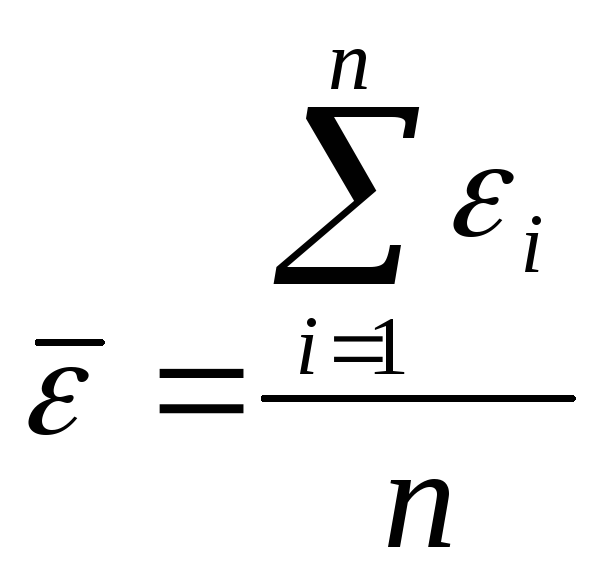
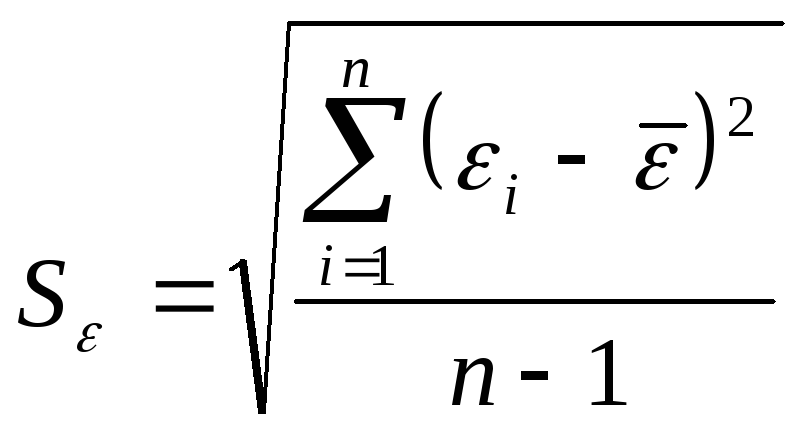
ε – среднее арифметическое значение;

S_ε – стандартное среднеквадратическое отклонение для этой последовательности.

Если расчетное значение t меньше табличного значения по статистике Стьюдента с заданным уровнем значимости α и числом степеней свободы к = n – 1, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается. В противном случае - отвергается, и модель считается неадекватной.

4.5. Проверка независимости значений уровней случайной компоненты.

Эта проверка проводится для выявления автокорреляции остатков.

Если ρ – положит., то автокорреляция «+»

Если ρ – отрицат., то автокорреляция «-»

Эта проверка может производиться по ряду критериев.

Наиболее распространенным является d-критерий Дарбина - Уотсона. Расчетное значение этого критерия находится по формуле:

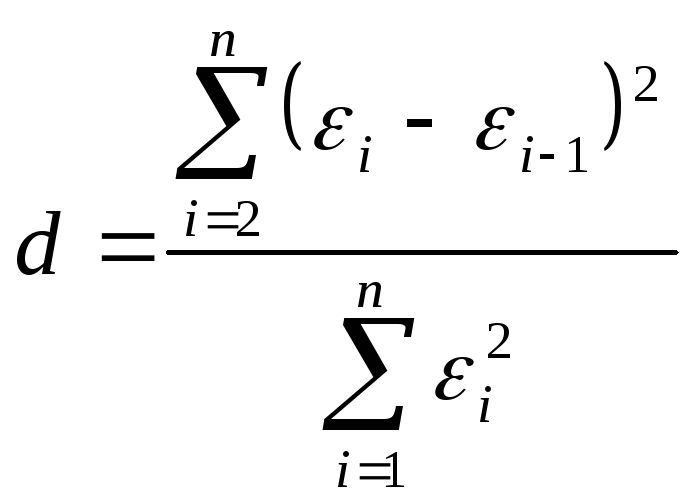
d-крит. изменяется от 0 до 4, если от 0 до 2 – положительная автокорреляция, если, расчетное значение d-критерия в интервале от 2 до 4 свидетельствует об отрицательной связи. В этом случае его надо преобразовать по формуле:

d' = 4 - d

и в дальнейшем использовать значение d' Расчетное значение критерия d или d' сравнивается с верхним d₂ и нижним d₁ критическими значениями статистики Дарбина - Уотсона. Если dp>d2 автокорреляцией можно пренебречь с вероятностью 95%.

Если расчетное значение критерия d больше верхнего табличного значения d₂, то гипотеза о независимости уровней остаточной последовательности, то есть об отсутствии в ней автокорреляции принимается.

Если расчетное значение d меньше нижнего табличного d₁ то эта гипотеза отвергается и модель считается неадекватной.

Если значение d находится между значениями d₁ и d₂, включая сами эти значения, то считается, что нет достаточных оснований делать тот или иной вывод и необходимы дальнейшие исследования, например по большему числу наблюдений.