33

Учебное пособие по эконометрике Глава 9. Основные положения теории множественной корреляции

9.1 Метод наименьших квадратов (мнк)

В случае корреляционной зависимости каждому аргументу X соответствует не одно строго определенное значение функции Y, что характерно для функциональной зависимости, а ряд распределений ее величины. Говоря более строго: Y находится в корреляционной зависимости от X, если каждому значению аргумента X соответствует ряд распределений функции Y. С изменением X эти ряды закономерно изменяют свое положение.

Функция Y = f (X) называется регрессией Y на X.

Линия регрессии показывает, как смещаются ряды распределения Y с увеличением X или как в среднем изменяется Y с изменением X.

В зависимости от того, рассматривается один или несколько аргументов, или так называемых факториальных признаков корреляционной функции регрессия называется простой (парной) или множественной (многофакторной).

Для практики экономического анализа и планирования наибольшее значение имеет множественная регрессия. В наиболее общем виде задача множественной регрессии заключается в следующем: имеется достаточно мощная статистическая совокупность, распределенная по (m+1) признакам, один из которых – Y, результативен, а остальные – X_j-тые – факториальные.

Требуется найти корреляционную функцию:

Y = f (X₁,X₂,…, X_m),

то есть уравнение регрессии, которое как можно лучше аппроксимирует исходный статистический материал.

Задачу нахождения регрессии можно также сформулировать в следующем виде:

Y_i = f (Xi, a₀, a₁,…а_j…,a_p), i=1÷ n, j=0 ÷ p

где X_i и Y_i - соответствующие друг другу измеренные значения, а n – число

измерений;

a_j= a₀,…,a_p – параметры уравнения регрессии.

Если бы значения X и Y находились точно, то для отыскания (p+1) параметра достаточно произвести (p+1) измерение.

На самом деле значения X и Y содержат ошибки или не учитываются все факторы, влияющие на Y. Следовательно, никакие (p+1) измерения не позволяют определить истинное значение параметров. Поэтому производится значительно большее число измерений. В результате чего число уравнений будет больше, чем число неизвестных параметров. В этом случае система уравнений будет несовместной, то есть точное решение какого-либо из набора (р+1) уравнения системы может не удовлетворять остальным уравнениям.

Задача состоит в том, чтобы найти такие значения неизвестных параметров, которые будут удовлетворять этим уравнениям наилучшим образом, хотя и неточно. Иначе говоря, требуется найти наиболее вероятные значения неизвестных параметров. Эти вероятные значения будут тем более близки к истине, чем больше число наблюдений. Так как уравнение удовлетворяется неточно, то можно записать:

Y_i - f (Xi, a₀, a₁,…,a_p) = ε_i, i=1÷n

где ε_i – отклонение измеренных значений Y_i от вычисленных по формуле.

Принцип наименьших квадратов утверждает, что наивероятнейшими значениями параметров a_j , будут такие, при которых сумма квадратов отклонений будет наименьшая:

Рассматривая здесь a₀, a₁,…,a_p как зависимые переменные и приравнивая к нулю частные производные от левой части уравнения по этим переменным, получим в точности (р+1) уравнение с (р+1) неизвестными. Составление и решение этой системы особенно просто в том случае, когда функция линейна относительно параметров, то есть можно записать:

(Xi, a₀, a₁,…,a_p) = φ₀(x) a₀+φ₁(x) a₁+ …+ φ_p(x) a_р

В этом случае данное уравнение может быть записано в следующем виде:

Дифференцируя вышеприведенное уравнение по a₀, a₁,…,a_p и приравнивая к 0 производные, получим систему уравнений:

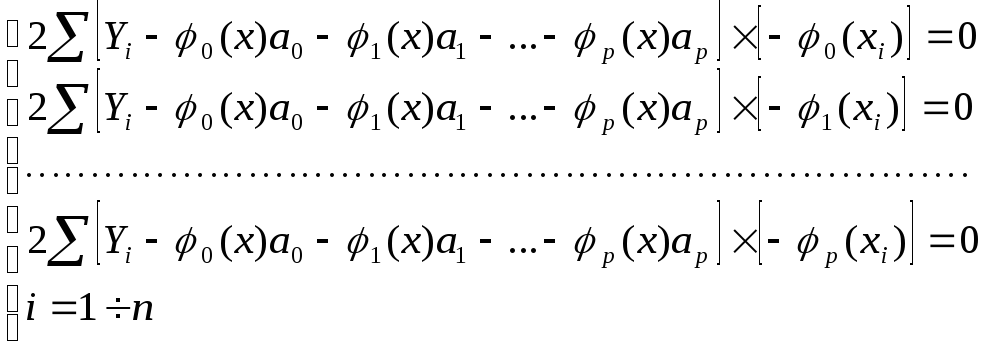
Вводя для краткости обозначения:

Получим из системы уравнений:

Данная система уравнений – это линейная система уравнений, решение данной системы может быть произведено одним из известных методов решений систем линейных алгебраических уравнений. Эта система уравнений называется системой в нормальной форме.