12.2 Линеаризация уравнения регрессии с использованием логарфмического преобразования (степенные и показательные функции).

В тех случаях, когда связь между фактор-ми перем-ми и результ-им приз-ом имеет вид степенного ур-ия (мультиколлин-ая функция) линеализация произв-ся путем логарифмирования исх. ур-ия.

12.3 Представление случайного члена в преобразованных нелинейных ур-ях регрессии.

(1)

(2)

Если в (1) удовл-ет четырем условиям случайности, т. е. мат. ожид-е =0, независимо др. от друга, то случ. Составляющая во (2) также будет удовл-ть этим усл-ям, и найденные из (2) с пом. МНК оценки параметров будут несмещ-ми, состоят-ми и эффектив-ми оценками. Если будем иметь ур-ие вида:(3), то случ. состав-ая должна входить как сомножитель.

(4)

Четырем усл-ям случайности должен удовл-ть lnδ_i, а самоδ_i подчин.др. законам. Н-р,

В получаемые с пом. МНК оценки состоятельные и эфектив-ые для ур-ия (4) и все стат. критерии справедливы для лин-го аддитивного ур-ия (4).

12.4 Определение параметров нелин-го ур-ия герессии, не приводимого к лин-му ур-ию.

Возьмем ур-ие: .Данное ур-ие не м. б. приведено к лин-му путем замены переменных или логарифмированием. Для оценки парам-ов данного ур-ия также используемметод минимизации суммы квадратов отклонений. Алгоритм нах-ия парам-ов α иbпредставим в виде послед-ти процедур:

1) примем некоторые правдоподобные исходн. знач-я α и b(α =1÷10,b= 0 ÷ 1,α⁰ =1,b=0,5)

2) исп-уя эти знач-я, найдем теоретич. знач-я и вычислим

3) вычислим

4)сделаем небольшой шаг по параметру α: Δ α =1+0,1= 1,1 и снова найдем величину μ⁽²⁾. Если μ⁽²⁾< μ⁽¹⁾ , то шаг сделан в правильном направлении.

5) продолжаем увелич-ть α в дан. напр-ии по шагам до тех пор, пока μ не начнет расти.

6) аналогич-ую процедуру проводим с параметром bфиксиров. α.

7) фиксируем найденное bи снова начинаем изменять α. Процедура повтор-ся до тех пор, пока любые измен-ия α иbне будут приводиь к увнлич-ю μ.

12.5 Выбор вида ур-ия регрессии с использ-ем теста Бокса-Кокса.

Исп-ие нелин-ых ур-ий для построения ур-ия регрессии значит-но повышает универс-сть регр-го анализа, но и усложняет задачу исслед-ля, т.к. усложняется проблема спецификации ур-ия регрессии. Если мы имеем дело с парной регрессией, то вид ур-ия м.б. решен (выбран) путем построения графика зависимости у = f(x) и по виду этого графика можно дост-но просто выбрать ур-ия. Однако в случае множ-ой регрессии такой подход практич-ки невозможен. В этом случае часто задача решется путем подбора подходящей функции и в качестве критерия оптим-ти используют коэф-т множ-ой детерминацииR², иногда сумма квадратов отклонений. Такой подход неправомерен, если сравниваются принципиально различ-е функц-ые зависимости. Н-р: лин-ая аддитивная модель(1)

мультипликтивная модель (2)

Использовать для срав-ия этих моделей сумму кавдратов отклонений невозм-но, т. к. lny_i ≠ y_i, а значит-но < его

(3)

Величина R² также не может быть использ-на, хотя она и безразмерна, т. к. она относ-ся к разным понятиям. В (1) она объясняет дисперсию у, объясн-ую дисперсией факториальных приз-ов (х₁и х₂). Во (2) она объясняет дисперсиюlny, вызванную дисперсиейlnх₁илиlnх₂. В тех случаях, когдаR² у одной модели значит-но >, чем у другой, тогда можно обоснованно осущ-ть выбор в пользу этой модели. Однако в тех случаях, когдаR²одной и др. модели соизмеримы др.с другом, то проблема выбора усложняется. В этом случае предлагается для выбора исп-тьтест Бокса-Кокса(это в общем случае). Для сравнения моделей (1) и (2) Пол Зарембко предложил упрощение теста Бокса-Кокса в 1968г. Суть теста в этом сл. след-ая:

1. исход-ые данные по у исп-ся для вычисления средней геометрической

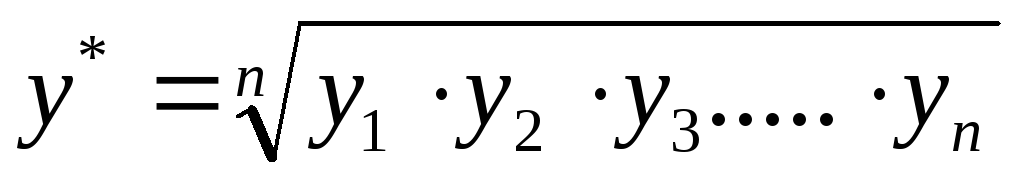
2. значение у персчит-ся с исп-ем

3. исп-ие нов. знач-я у находим параметры (оценки) ур-ия (1). А исп-уя lny’из ур-ия (3) нах-ся оценки а_о,β₁,β₂.Для этих двух моделей (1) и (3) нах-ся сумма квадратов отклонений. Эти суммы являются сопоставимыми и след-но та модель, которая дает меньшую сумму квадратов отклонений и признается лучшей.

4. для того, чтобы окончат-но решить вопрос, что действительно одна из моделей дает лучшее соответ-ие, рассчит-ся пок-ль:, где Т-число набл-й (n),Z-отнош-е ∑ кв. отклонений в 1 и 2 ур-ии.. Х²_расч. сравнив-ся с табличным. Данное стат. распределение им. одну степень свободы и разное знач-е уровня значимости, если Х²_расч. > Х²_табл. при 5 %-значимости, то действ-но одна из моделей сущ-но лучше другой.

1. Общая характеристика временных рядов. Трендовые модели.

Динамич. процессы, происх-ие в эк-их системах чаще всего проявляются в виде ряда послед-но располож-ых в хронолог-ом порядке знач-ий того или иного пок-ля, кот. в своих изменениях отражает ход развития изучаемого явления. Эти знач-я пок-ей могут служить основой для разработки прикладн. моделей особого вида, наз-ых трендовыми моделями. Послед-ть наблюдений одного пок-ля, упорядоч-ая в завис-ти от послед-но возраст-их или убывающих знач-ий др. показ-ля наз.динамическим рядом. Если в кач-ве приз-ка, в завис–ти от кот-го проис-ит упорядочеие, берется время, то такой динамич. ряд наз.временным рядом. Состав-ми элем-ми радов динамики явл. цифровые значения пок-ля, наз-ыеуровнемэтих радов и моменты или интервал времени, к кот. относ-ся эти уровни. Временные ряды образованные пок-ми. харк-ми эк. явления на опред. моменты времени над.моментными. Если уровни временного ряда образ-ся путем агрегирования за опред-ый промежуток времени, то такие рады наз-сяинтервальными врем. Рядами. Врем. Ряды могут быть образованы как из абсолютных знач-й эк. пок-ей, так и из средних относит-ых величин. Эти ряды наз.производными рядами. Поддлиной врем. рядапоним-ся время, прошедшее от начала момента набл-ия до конечного. Если во врем. ряду прояв-ся длит-ая тенденция изм-ия эк. пок-ля, то считается, что в этом имеется тренд. След-но подтрендомпоним-ся изменение, опред-ее общее направ-е развития, т. е. осн. тенденция врем. ряда. След-но, эк-ко-мат-ая динамич-ая модель, в кот. развитие эк. системы отраж-ся через тренд ее осн. показ-ей наз.трендовой моделью. Отличие врем. эк. радов от простых стат. совокуп-ей закл-ся прежде всегов том, что послед-ые знач-я уровня временного ряда зависят друг от друга, т. е. имеется существенная автокорел-ия между уровнями ряда (не остатков, а х). В связи с этим выводы и формулы ТВ и МС могут исп-ся с большей осторожностью. Любой врем. ряд эк. пок-ей можно разложить на 4 составл-ие:, где Т-тренд,S-сезонная сост-ая, С-циклич-ая сост-ая,-случ-ая сост-ая. При построении трендовых моделей необходимо, чтобы дан. Модельсущ-ым образом отражала изменения систематич-их компонент врем. ряда. (Т,S,C). Случ. сост-ая () для адекватных моделей должна подчиняться 4 св-ам Гаусса-Марка (2 лаб. Работа):1) случай-ть колеб-й; 2) мат. ожидание = 0; 3) норм-ый закон распр-ия; 4) независ-ть.- трендовая модель.

2. Предварительный анализ временных рядовю. Метод Ирвина.

Предвар-ый анализ врем. рядов эк. показ-ей закл. в основном выявлении и устранении аномальных зн-ий уровней ряда, а также определении наличия тренда в исх-ом врем-ом ряде. Под аномальными уровнямипоним-ся отдельное знач-е уровня врем. ряда, кот. не отвечает потенц. возм-ям ислед-ой эк. системы и, оставаясь в качестве ур-ня ряда,, оказ-ет сущест-ое влияние на знач-е осн-ых характер-ик вр. ряда. Причинами аномальных наблюдений м. б.ошибки технич-го порядка или ошибки первого рода. Такие ошибки подлежат выявлению и устранению. Однако аномальные уровни во врем. рядах могут возникать из-за возд-ия факторов, имеющих объективный хар-р, проявл-ся эпизодич-ки (т. е. редко) – это ошибки второго рода, и они устранению не подлежат. Для выявл-я аномальных уровней врем. ряда исп-ся методы, рассчит-ые для стат. 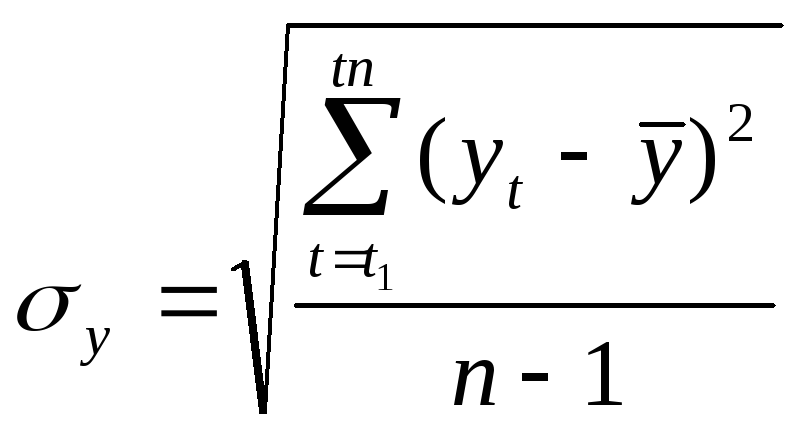совок-ей, в частности м-д Ирвина:λ=0,05 (т.е 5% уровень знач-ти 0 гипотезы). После выявления аном. уровней изучаемого ряда необх-мо выявить причину возн-ия этого аномальн. уровня. Если аном-ое набл-ие вызвано ошибкой первого рода, то они устран-ся путем замены этого аном-го набл-ия сред-им арифм-им знач-ем, получ-ым из аппроксимирующей кривой для данного врем-го ряда.

3. Сглаживание временных рядов экономич. показ-ей.

Часто уровни эк. рядов динамики колеб-ся. При этом тенденция развития эк. явления во времени скрыта случ. отклонениями ур-ня в ту или иную стороны с целью более четкого появления тенденции развития исслед-го процесса. В том числе для дальнейшего примен-я мет-ов прогнозир-ия на основе тренд. моделей производит сглаживание вр. рядов. Методы сглаж-я дел-ся на 2 большие группы:

1) аналитическое выравнивание с исп-ем кривой, отображ-ей осн. тенденцию вр. ряда (измен. вр. ряда).

2) механич-ое выравнивание отдельн. уровней вр. ряда с использованием фактич. знач-й соседних уровней.

Методы аналитич-го выр-иябазируются на применении разл-го вида полиномов и нах-ии коэф-ов этих полиномов МНК. В кач-ве поиномов исп. либо степен. Чебышева поиномы, рад Фурье.

Суть механич-го сглаж-ия зак-ся в след.:берется неск-ко 1-ых Ур-ей вр. ряда,образующих интервал сглаж-ия. Для них подбир. полином, степень кот-го должна быть< числа уровней, входящих в интервал сглаживания. С пом. полинома опр-ся нов. выровненные знач-я уровней в середине интервала сглаж-ия. Затем интервал сглаж-я сдвиг-ся на 1 уровень ряда вправо и вычисл-сяслед-ее сглаженное знач-е и т. д. Самым простым методом мех-го сглаж-я явл.метод простой скользящей средней.В данном методе для уровней ряда у₁, у₂, у₃…у_n опред-ся интервал сглаж-яm<n. Если необх-мо сгладить как можно больше колебаний, то инт-ал сглаж-ия берут по возможности большим. Если необх-мо сохранить колеб-ия опред-ой частоты, то инт-ал сглаж-ия уменьшают. Желат-но инт-ал сглаж-ия брать нечетным. Для первыхm-уровней вычисл-ся ср. арифм. Это будет сглаженное знач-е для середины инт-ла сглаж-ия. Затем интервал сдвиг-ся вправо на 1 уровень. Для высисл-я сглаж-ых знач-й исп-ся формула:. В рез-те получается (n-m+1) – сглаженных знач-й. При этом первые и послед-ие р-уровни ряда не сглаж-ся. Данный метод обычно исп-ют дл рядов, имеющих лин. тенденцию.

Метод взвешенной скользящей средней: отлич от предыдущего тем, что уровни ряда, вход-ие в интервалсглаж-ия суммируются с разн. весами и аппроксимация ряда в пределах инт-ла сглаж-ия осущ-ся с исп-ем полиномов степени от 2 и више. Опред-ие сглаж-го знач-я в этом случае опред-ся по фор-ле:, где ρ – веса разл. уровней ряда в сглаж-ом знач-ии. Эти веса (ρ) опр-ют с пом. МНК,они приводятся в соотв-ии справочн табл.

Метод экспоненциального сглаж-ия:Особ-тью данного метода явл. то, что при нахождении степенного ур-ня исп-ются знач-ия только предшеств-их уровней ряда, взятых с опред-ым весом, причем вес наблюдения уменьш-ся по мере удаления его от момента времени, для кот-го опред-ся сглаж-ие знач-ия уровня ряда.

В данном методе, если обозначить через S_tсглаж-ие зная-ия, где α-парам-рсглаж-ия 0< α <1, (α-1) – коэф-т дисконтир-ия. Экспоненциальная средняя явл. взвеш-ой средней всех предыдущих уровней ряда. Эмпирически рекомендуется выбирать α ≈ (0,1÷0,3). В некот-х рекомендациях берут. Начальное значение (S_о) обычно вычисл-ся как ср. арифм-ое первых членов ряда..