17. Достаточное условие дифференцируемости функций многих переменных.

Теорема 5. Если функция f:V(x)→R,V(x) С Rⁿ имеет в окрестности V(x) точки x все частные производные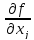,j=1,n, непрерывные в точке x, то она дифференцируема в этой точке.

Доказательство. Без ограничения общности будем считать, что V(x)является шаром B(x,r).Тогда вместе с точками x=(x₁,...,x_n),x+h=(x₁+h₁,...,x_n+h_n)области V(x)должны принадлежать также точки (x_i, x₂ + h₂, …,x_n+ h_n),...,(x₁, x₂,...,x_n-1, x_n+h_n)и соединяющие их отрезки. Воспользуемся этим, применяя теорему Лагранжа для функции одной переменнойf(x+h)—f(x)=f(x₁+h₁,...,x_n+h_n)—f(x₁, ...,x_n)=f(x₁+h₁,...,x_n+h_n)—f(x₁,x₂+h₂,...,x_n+h_n)+f(x₁,x₂+h₂,...,x_n+h_n)—f(x₁,x₂,x₃+h₃,...,x_n+h_n)+...+f(x₁,x₂,...,x_n-1,x_n+h_n)—f(x₁,x₂, ...,x_n)=где воспользовались наличием у функции fв области V(x)частных производных по каждой из переменных. Сейчас воспользуемся их непрерывностью в точке x. Продолжая предыдущие преобразования, получаем, что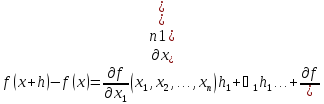, где величины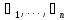в силу непрерывности вточкеx стремятся к нулю при h →0.

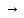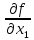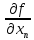Но это означает, что f(x+ h)—f(x)= L(x)h+ o(h)при h0, где L(x)h=(x₁,x₂,...,x_n)h₁+ ...+(x₁,x₂,...,x_n)h_n

18.Производная по направлению. Градиент.

Опр.1 Если существует предел 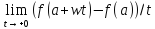,то он называется производной функцииf по направлению вектора w в точке a и обозначается .

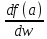Если w=e_j, j=1,n где e_j координатный вектор пространства Rⁿ, то =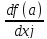, т.е. частные производные функцииf в точке а являются производными этой функции в точке а по направлению соответствующих координатных осей.

Опр.2. Вектор (, …, 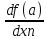) называется градиентом функции f в точке а и обозначается grad f(a).

Теорема6. Если функция f: X→R, XCRⁿ дифференцируема в точке аϵХ, то она имеет в этой точке производные по любому направлению , причем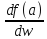=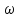*grad f(a).

Доказательство. Поскольку функция f дифференцируема в точке а то

f(a+wt)-f(a)=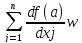_jt+o(wt), t→+0.

Разделив обе части соотношения на t, и затем перейдя к пределу при t→+0, получим

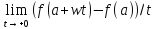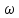==_j=*grad f(a),

Т.к. =0.

19. Частные производные высших порядков.

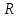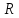Пусть функция f:X→, X С ⁿимеет частную производную 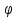= 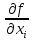в области X. Если существует частная производная 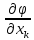, то она называется второй частной производной или частной производной второго порядка функцииfпо переменным x_i, x_kи обозначается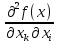или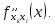Частная производная по некоторой переменной от частной производной (т—1)-го порядка называется частной производной порядка m. Частная производная по различным переменным называется смешанной частной производной. Частная производная высшего порядка по одной и той же переменной называется чистой частной производной.

Теорема 7. Пусть функция f:V(a,δ)→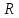,V(a,δ) С 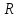ⁿимеет в окрестности V(a,δ) точки a частные производные причем они непрерывны в точкеa. Тогда справедливо равенство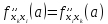. (1)

Доказательство. Рассмотрим вспомогательное соотношение

w=f(a+h_ke_k+h_ie_i)-f(a+ h_ke_k)-f(a+ h_ie_i)+f(a) (2)

Его можно рассмотреть как приращение функции 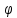=f(х+ h_ke_k)-f(x) по переменной x_i в точке а. По теореме Лагранжа получим w=(f’_xi(a+h_ke_k+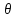₁ h_ie_i)- f’_xi (a+ 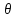₁h_ie_i))h_i, (3)

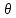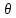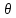где 0<₁<1. Рассмотрим содержащаяся в скобках соотношения (3), является приращением функции f’_xi по переменной x_k в точке a+₁h_ie_i.Применяя вновь теорему Лагранжа, получим w=f”_xixk(a +₁ h_ie_i+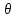₂h_ke_k)hihk, (4) где 0<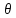₂<1. Если соотношение (2) рассмотреть вновь как приращение функции 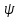=f(х+ h_ie_i)-f(x) по переменной x_k в точке а, то рассуждая аналогично получим, что

w=f”_xkxi(a +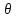₃h_ke_k+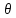₄ h_ie_i)h_kh_i, (5) где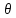 0<₃<1, где 0<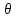₄<1.

Из (4) и (5) имеем:

f”_xixk(a +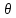₁ h_ie_i+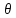₂h_ke_k)= f”_xkxi(a +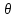₃h_ke_k+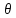₄ h_ie_i) (6)

Поскольку 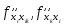непрерывны в точке а, то переходя в (6) к пределу приh_i→0, h_k→0, получим (1).

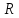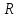Утверждение 3. Если f:X→, X Сⁿимеет в области X непрерывные частные производные до порядка к включительно, то частная производная функции f к-го порядка не зависит от порядка дифференцирования.