
- •1.Несобственные интегралы и их свойства.
- •3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
- •4.Предельный признак сравнения
- •6.Признак Абеля
- •7. Метрическое пространство . Некоторые топологические понятия
- •8.Евклидово пространство .
- •9. Последовательности точек пространства .
- •10. Предел отображения.
- •11. Предел по направлению. Повторные пределы.
- •12.Локальные свойства непрерывных отображений.
- •13.Глобальные свойства непрерывных отображений.
- •14. Линейные отображения.
- •15. Дифференцируемые отображения.
- •16.Свойства дифференцируемых отображений.
- •17. Достаточное условие дифференцируемости функций многих переменных.
- •18.Производная по направлению. Градиент.
- •19. Частные производные высших порядков.
- •20.Формула Тейлора для функций многих переменных.
- •21. Необходимые условия экстремума.
- •22. Достаточные условия локального экстремума.
- •23. Неявные функции.
- •24. Обратное отображение.
- •25. Необходимые условия зависимости функций.
- •26. Достаточные условия зависимости функций.
- •27. Понятие условного экстремума.
- •28. Метод множителей Лагранжа.
- •29. Числовые ряды. Критерий Коши
- •30.Признаки сравнения сходимости числовых рядов.
- •31. Признаки Даламбера и Коши сходимости рядов.
- •32. Интегральный признак сходимости ряда.
- •33. Знакочередующиеся ряды.
- •34.Признак Абеля и Дирихле.
- •35. Абсолютно и условно сходящиеся числовые ряды
- •36. Перемножение абсолютно сходящихся числовых рядов.
- •37. Бесконечные произведения.
- •38. Равномерная сходимость функциональных рядов и последовательностей.
- •39.Признаки равномерной сходимости функц. Рядов.
- •41. Непрерывность суммы ряда.
- •42.Интегрирование равномерно сходящихся рядов и последовательностей
- •43. Дифференцирование равномерно сходящихся рядов.
- •44. Степенной ряд, радиус сходимости.
- •45. Формула Коши-Адамара
- •46.Почленное дифференцирование и интегрирование степенных рядов.
- •47. Аналитические функции. Ряд Тейлора.
- •48. Ряды Тейлора основных элементарных функций.
- •49.Ряды Фурье по ортонормированной системе функций.
- •50. Интеграл Дирихле.
- •51. Сходимость рядов Фурье в точке(лемма 1)
- •52. Признак Дини и следствия из него
- •53. Суммирование рядов Фурье методом средних арифметических.
- •54. Теорема Фейера.
- •55. Теорема Вейерштрасса.
- •56. Неравенство Бесселя. Равенство Парсеваля.
- •57.Диф. Тригонометрических рядов Фурье.
- •58. Интегрирование рядов Фурье
- •59.Комплексная форма ряда Фурье.
36. Перемножение абсолютно сходящихся числовых рядов.
Теорема
16.
Если
ряды (1)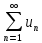 и (2)
и (2)
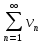 абсолютно
сходятся, то ряд, составленный из
всевозможных произведенийukvl,
к
=1,
2,
..
., l=1,
2,
..
., расположенных
в любом порядке также абсолютно сходится,
причем его сумма S=
u•
v,
где u,
v—
суммы рядов (1) и (2) соответственно.
абсолютно
сходятся, то ряд, составленный из
всевозможных произведенийukvl,
к
=1,
2,
..
., l=1,
2,
..
., расположенных
в любом порядке также абсолютно сходится,
причем его сумма S=
u•
v,
где u,
v—
суммы рядов (1) и (2) соответственно.
Доказательство.
Рассмотрим ряд
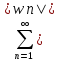 (3)
где wn,
n=1,2,..
произведения вида ukvl,
k=1,2,..,
l=1,2,…
Пусть Gn
n-ая
частичная сумма ряда (3). Через m
обозначим наибольшее из индексов k,l
членов ряда входящих в Gn.
Тогда Gn≤(
(3)
где wn,
n=1,2,..
произведения вида ukvl,
k=1,2,..,
l=1,2,…
Пусть Gn
n-ая
частичная сумма ряда (3). Через m
обозначим наибольшее из индексов k,l
членов ряда входящих в Gn.
Тогда Gn≤(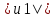 +…+
+…+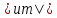 )(
)(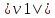 +…+
+…+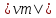 )
)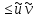 ,n=1,2,…
,n=1,2,…
где
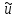 =
= ,
,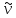 =
=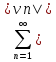 .
.
Следовательно
критерию сходимости ряда с неотрицательными
членами ряд (3) сходится. В силу теоремы
о перестановке членов числового ряда
сумма абсолютно сходящегося ряда
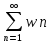 не зависит от порядка его членов. Поэтому
можно выполнить такую перестановку его
членов, чтоGn2=(
не зависит от порядка его членов. Поэтому
можно выполнить такую перестановку его
членов, чтоGn2=( +…+
+…+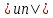 )(
)(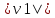 +…+
+…+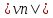 )(4)
)(4)
где
Gn2
частичная
сумма ряда
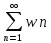 .
Переходя в (4) к пределу приn→∞
получим S=u*v.
Т.о. абсолютно сходящиеся ряды можно
перемножать.
.
Переходя в (4) к пределу приn→∞
получим S=u*v.
Т.о. абсолютно сходящиеся ряды можно
перемножать.
37. Бесконечные произведения.
Определение
1. Пара
последовательностей {un},
Un€R,
n=
1, 2,...
и
{Pn}
где
Pn=
u1•
u2•
...
•
unназывается
бесконечным произведением и обозначается
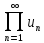 .(1)
.(1)
свойства бесконечных произведений. Выражение qn= un+1• un+2• ... называется n-ым остаточным произведением.
1°. Если бесконечное произведение сходится, то любое его остаточное произведение сходится. Если какое-либо остаточное произведение сходится то и само бесконечное произведение сходится. Следовательно, отбрасывание или присоединение конечного множества отличных от нуля первых сомножителей не влияет на сходимость бесконечного произведения.
2°.
Если
бесконечное произведение (1) сходится,
то предел его остаточного произведения
limqn=
1.(n→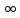 )
)
3°
(Необходимое
условие сходимости бесконечного
произведения.) Если
бесконечное произведение сходится, то
limun=
1.(n→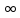 )
)
Теорема
18. Бесконечное
произведение (1) у которого un>0,
n=
1, 2,..
. сходится
тогда и только тогда, когда сходится
ряд
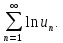 (2)
(2)
В случае сходимости сумма S ряда (2) и значение P бесконечного произведения (1) связаны соотношением P=eS.(3)
Доказательство.
Пусть
Pn—
n-ое
частичное произведение для (1), Sn—
n-ая
частичная сумма для ряда (2). Тогда
lnPn=
Sn,
откуда
Pn=
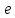 Sn.
Переходя к пределу при n→
Sn.
Переходя к пределу при n→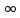 получим
утверждение теоремы и формулу (3).
получим
утверждение теоремы и формулу (3).
Теорема
19. Если
un>=0
или
un<=0,
n=
1, 2, ..
. то
бесконечное произведение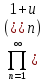 (4)сходится
тогда и только тогда, когда сходится
ряд
(4)сходится
тогда и только тогда, когда сходится
ряд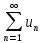 (5)
(5)
Доказательство.
Условие
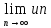 =0
является необходимым для сходимости
бесконечного произведения (4) для
сходимости ряда (5). Из этого условия и
равенства
=0
является необходимым для сходимости
бесконечного произведения (4) для
сходимости ряда (5). Из этого условия и
равенства
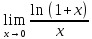 =1
следует, что
=1
следует, что
 =1(6)
Поскольку
члены ряда (4) и ряда
=1(6)
Поскольку
члены ряда (4) и ряда
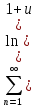 )
(7)
начиная
с некоторого номера n
сохраняют один и тот же знак, то в силу
(6) согласно предельного признака
сравнения ряды (5) и (7) сходятся и расходятся
одновременно. На основании теоремы 18
бесконечное произведение (4) и ряд (7)
сходятся и расходятся одновременно.
Поэтому бесконечное произведение (4) и
ряд (5) также будут сходиться и расходиться
одновременно.
)
(7)
начиная
с некоторого номера n
сохраняют один и тот же знак, то в силу
(6) согласно предельного признака
сравнения ряды (5) и (7) сходятся и расходятся
одновременно. На основании теоремы 18
бесконечное произведение (4) и ряд (7)
сходятся и расходятся одновременно.
Поэтому бесконечное произведение (4) и
ряд (5) также будут сходиться и расходиться
одновременно.
