
- •1.Несобственные интегралы и их свойства.
- •3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
- •4.Предельный признак сравнения
- •6.Признак Абеля
- •7. Метрическое пространство . Некоторые топологические понятия
- •8.Евклидово пространство .
- •9. Последовательности точек пространства .
- •10. Предел отображения.
- •11. Предел по направлению. Повторные пределы.
- •12.Локальные свойства непрерывных отображений.
- •13.Глобальные свойства непрерывных отображений.
- •14. Линейные отображения.
- •15. Дифференцируемые отображения.
- •16.Свойства дифференцируемых отображений.
- •17. Достаточное условие дифференцируемости функций многих переменных.
- •18.Производная по направлению. Градиент.
- •19. Частные производные высших порядков.
- •20.Формула Тейлора для функций многих переменных.
- •21. Необходимые условия экстремума.
- •22. Достаточные условия локального экстремума.
- •23. Неявные функции.
- •24. Обратное отображение.
- •25. Необходимые условия зависимости функций.
- •26. Достаточные условия зависимости функций.
- •27. Понятие условного экстремума.
- •28. Метод множителей Лагранжа.
- •29. Числовые ряды. Критерий Коши
- •30.Признаки сравнения сходимости числовых рядов.
- •31. Признаки Даламбера и Коши сходимости рядов.
- •32. Интегральный признак сходимости ряда.
- •33. Знакочередующиеся ряды.
- •34.Признак Абеля и Дирихле.
- •35. Абсолютно и условно сходящиеся числовые ряды
- •36. Перемножение абсолютно сходящихся числовых рядов.
- •37. Бесконечные произведения.
- •38. Равномерная сходимость функциональных рядов и последовательностей.
- •39.Признаки равномерной сходимости функц. Рядов.
- •41. Непрерывность суммы ряда.
- •42.Интегрирование равномерно сходящихся рядов и последовательностей
- •43. Дифференцирование равномерно сходящихся рядов.
- •44. Степенной ряд, радиус сходимости.
- •45. Формула Коши-Адамара
- •46.Почленное дифференцирование и интегрирование степенных рядов.
- •47. Аналитические функции. Ряд Тейлора.
- •48. Ряды Тейлора основных элементарных функций.
- •49.Ряды Фурье по ортонормированной системе функций.
- •50. Интеграл Дирихле.
- •51. Сходимость рядов Фурье в точке(лемма 1)
- •52. Признак Дини и следствия из него
- •53. Суммирование рядов Фурье методом средних арифметических.
- •54. Теорема Фейера.
- •55. Теорема Вейерштрасса.
- •56. Неравенство Бесселя. Равенство Парсеваля.
- •57.Диф. Тригонометрических рядов Фурье.
- •58. Интегрирование рядов Фурье
- •59.Комплексная форма ряда Фурье.
32. Интегральный признак сходимости ряда.
Теорема
10. Если
функция f:
[1;+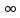 )
)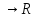 неотрицательна
и убывает на этом промежутке, то ряд
неотрицательна
и убывает на этом промежутке, то ряд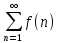 (1)
сходится
тогда и только тогда, когда сходится
несобственный интеграл
(1)
сходится
тогда и только тогда, когда сходится
несобственный интеграл
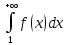 (2)
(2)
Доказательство:
Поскольку
функция fубывает
на промежутке [1; +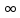 ),
тоf(к
+
1) <=f(x)
<=f(к),
к =1,
2,...,x€[к,
к +
1]. Проинтегрируем
это по отрезку x€[к,
к +1]
получим
),
тоf(к
+
1) <=f(x)
<=f(к),
к =1,
2,...,x€[к,
к +
1]. Проинтегрируем
это по отрезку x€[к,
к +1]
получим
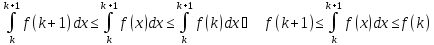 (3)
(3)
Просуммировав это неравенство отк = 1 до n, будем иметь
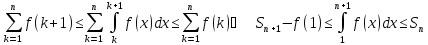 (4)
(4)
где
Sn-
частичная сумма ряда (1). Пусть ряд (1)
сходится и имеет сумму S.
ТогдаSn<=Sт.к.последовательность
{Sn}
не
убывает.Для любого
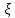 €[1;+oo)
найдется
такое n,
что n>=
€[1;+oo)
найдется
такое n,
что n>=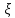 ,
поэтому из (3) и (4) имеем, что
,
поэтому из (3) и (4) имеем, что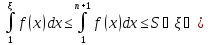 . Последнее означает, что несобственный
интеграл (2) сходится. Пусть несобственный
интеграл (2) сходится. Тогда
. Последнее означает, что несобственный
интеграл (2) сходится. Пусть несобственный
интеграл (2) сходится. Тогда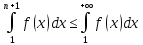 и,
в силу (3) имеем, что
и,
в силу (3) имеем, что
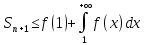 ,
n=1,2,…
,
n=1,2,…
Последнее означает, что последовательность частичных сумм ряда (1) ограничена сверху, т.е. ряд (1) сходится.
33. Знакочередующиеся ряды.
Теорема
Лейбница:
Если посл.
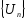 убывает и стремится к 0, т.е.
убывает и стремится к 0, т.е. ,
,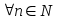 ,
,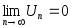 (1)
то ряд
(1)
то ряд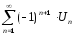 (2) сходится, причём если
(2) сходится, причём если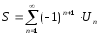 сумма ряда,
сумма ряда,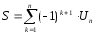 n-ая
частичная сумма ряда, то при
n-ая
частичная сумма ряда, то при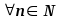 выполняется неравенство
выполняется неравенство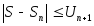 .
.
Доказательство:
Прежде всего, отметим, что из условия
(1)
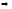
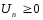 в силу чего члены ряда (2) поочерёдно то
>0, то <0. Ряды такого вида наз.
знакочередующимися. Частичные суммы
ряда (2) с чётными номерами возрастают
в силу чего члены ряда (2) поочерёдно то
>0, то <0. Ряды такого вида наз.
знакочередующимися. Частичные суммы
ряда (2) с чётными номерами возрастают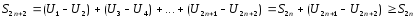
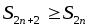 (частичные суммы с чётными номерами
возрастают)
(частичные суммы с чётными номерами
возрастают)
Кроме
того посл-ть
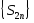 ограничена
сверху
ограничена
сверху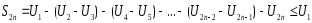
Поскольку
последовательность
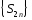 возрастает и ограничена сверху, то она
имеет конечный предел
возрастает и ограничена сверху, то она
имеет конечный предел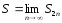
Покажем,
что тот же предел имеет посл-ть частичных
сумм с нечётными номерами
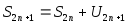 ,
а
,
а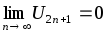 тогда
тогда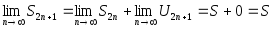 поэтому посл-ть
поэтому посл-ть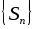 всех частных сумм ряда (2) имеет конечный
предел, при этом поскольку посл-ть
всех частных сумм ряда (2) имеет конечный
предел, при этом поскольку посл-ть возрастает то
возрастает то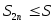 ,
посл-ть
,
посл-ть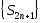 убывает, т.к.
убывает, т.к.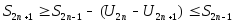 ,
поэтому
,
поэтому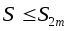 .
.
Таким
образом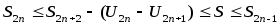 отсюда получаем
отсюда получаем
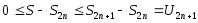 и
и
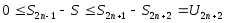 а это означает
а это означает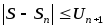
34.Признак Абеля и Дирихле.
Рассмотрим
ряды
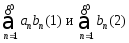
Теорема:
Признак Абеля. Если ряд (2) сходится, а последовательность
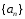 - монотонна и ограничена, то ряд (1)
сходится.
- монотонна и ограничена, то ряд (1)
сходится.Признак Дирихле. Если последовательность
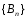 частичных сумм ряда (2) ограничена, а
последовательность
частичных сумм ряда (2) ограничена, а
последовательность монотонно стремится к нулю, то ряд (1)
сходится
монотонно стремится к нулю, то ряд (1)
сходится
Доказательство: Согласно критерию Коши:
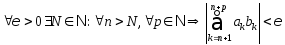
Полагая
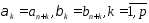 ,
запишем
,
запишем
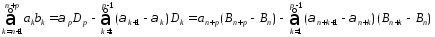
т.к.
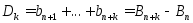 и
и
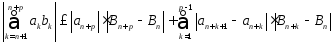 (3)
(3)
1)
Из условия признака Абеля следует, что
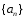 ограничена, т.е.
ограничена, т.е.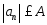 и ряд (2) сходится а значит по критерию
Коши
и ряд (2) сходится а значит по критерию
Коши
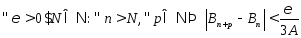
Тогда получим, что
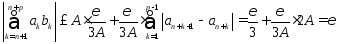
т.к.
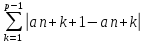 ≤
2A
в силу монотонности посл {an}
и ее ограниченности. Согласно критерию
Коши ряд (1) в рассматриваемом случае
сходится.
≤
2A
в силу монотонности посл {an}
и ее ограниченности. Согласно критерию
Коши ряд (1) в рассматриваемом случае
сходится.
2)
Из условия признака Дирихле следует,
что
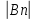 ≤M,
n=1,2,..
(т.к. {Bn}
ограничена) и
≤M,
n=1,2,..
(т.к. {Bn}
ограничена) и
 ε>0
ε>0
 N
N N:
N: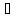 n>N→|an|<
n>N→|an|<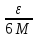 ,(т.к. an→0)
Тогда учитывая (3) будем иметь
,(т.к. an→0)
Тогда учитывая (3) будем иметь
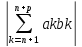 ≤
≤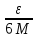 *2M+2M
*2M+2M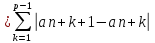 ≤
≤
≤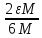 +2M*
+2M*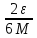 =ε
=ε
(где использовалась монотонность последовательности {an}), т.е. ряд (1) сходится.
35. Абсолютно и условно сходящиеся числовые ряды
Пусть
дан ряд
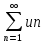 (1). Рассмотрим
ряд
(1). Рассмотрим
ряд
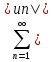 (2)
(2)
Теорема13. Если ряд (2) сходится, то сходится и ряд (1). Доказательство. Поскольку
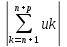 =
=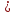 un+1+
un+2
+…+un+p
un+1+
un+2
+…+un+p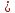 ≤
≤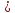 un+1
un+1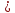 +
+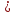 un+2
un+2
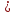 +…+
+…+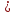 un+p
un+p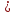 =
=
=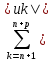 <ε,
то согласно критерию Коши следует
справедливость утверждения теоремы.
<ε,
то согласно критерию Коши следует
справедливость утверждения теоремы.
Опр.1. Если ряд (2) сходится, то ряд (1) наз. абсолютно сходящимся.
Опр.2. Если ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.
Теорема14. Если ряд (1) абсолютно сходится, то при любой перестановке его членов получим новый ряд, который также абсолютно сходится и имеет ту же сумму.
Док-во.
Введем обозначения un+=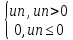 ,
,
un-
=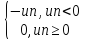 .
Тогда
un=
un+
- un-,
n=1,2,…
Поскольку
un+≤
.
Тогда
un=
un+
- un-,
n=1,2,…
Поскольку
un+≤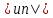 ,
un-
≤
,
un-
≤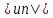 ,
n=1,2,…
и ряд (1) сходится абсолютно, то по признаку
сравнения сходятся ряды
,
n=1,2,…
и ряд (1) сходится абсолютно, то по признаку
сравнения сходятся ряды
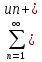 (3)
и
(3)
и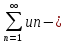 (4) с
неотрицательными членами. При некоторой
перестановке членов ряда (1) получим ряд
(4) с
неотрицательными членами. При некоторой
перестановке членов ряда (1) получим ряд
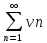 , а из рядов (3) и (4) получим соответственно
ряды
, а из рядов (3) и (4) получим соответственно
ряды
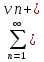 (5)
и
(5)
и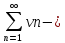 (6) где
vn+,
vn-
определяются аналогично un+
, un-.
В силу теореме о перестановке членов в
рядах с неотрицательными членами ряды
(5) и (6) сходятся и имеют ту же сумму, что
и ряды (3) и (4) соответственно. тогда
согласно теореме о сумме числовых рядов
имеем
(6) где
vn+,
vn-
определяются аналогично un+
, un-.
В силу теореме о перестановке членов в
рядах с неотрицательными членами ряды
(5) и (6) сходятся и имеют ту же сумму, что
и ряды (3) и (4) соответственно. тогда
согласно теореме о сумме числовых рядов
имеем
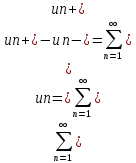 -
-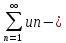 =
=
=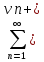 -
-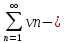 =
=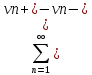 =
=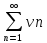
Т.о.
показали, что ряд
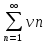 имеет ту же сумму, что и ряд (1)
имеет ту же сумму, что и ряд (1)
