
- •1.Несобственные интегралы и их свойства.
- •3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
- •4.Предельный признак сравнения
- •6.Признак Абеля
- •7. Метрическое пространство . Некоторые топологические понятия
- •8.Евклидово пространство .
- •9. Последовательности точек пространства .
- •10. Предел отображения.
- •11. Предел по направлению. Повторные пределы.
- •12.Локальные свойства непрерывных отображений.
- •13.Глобальные свойства непрерывных отображений.
- •14. Линейные отображения.
- •15. Дифференцируемые отображения.
- •16.Свойства дифференцируемых отображений.
- •17. Достаточное условие дифференцируемости функций многих переменных.
- •18.Производная по направлению. Градиент.
- •19. Частные производные высших порядков.
- •20.Формула Тейлора для функций многих переменных.
- •21. Необходимые условия экстремума.
- •22. Достаточные условия локального экстремума.
- •23. Неявные функции.
- •24. Обратное отображение.
- •25. Необходимые условия зависимости функций.
- •26. Достаточные условия зависимости функций.
- •27. Понятие условного экстремума.
- •28. Метод множителей Лагранжа.
- •29. Числовые ряды. Критерий Коши
- •30.Признаки сравнения сходимости числовых рядов.
- •31. Признаки Даламбера и Коши сходимости рядов.
- •32. Интегральный признак сходимости ряда.
- •33. Знакочередующиеся ряды.
- •34.Признак Абеля и Дирихле.
- •35. Абсолютно и условно сходящиеся числовые ряды
- •36. Перемножение абсолютно сходящихся числовых рядов.
- •37. Бесконечные произведения.
- •38. Равномерная сходимость функциональных рядов и последовательностей.
- •39.Признаки равномерной сходимости функц. Рядов.
- •41. Непрерывность суммы ряда.
- •42.Интегрирование равномерно сходящихся рядов и последовательностей
- •43. Дифференцирование равномерно сходящихся рядов.
- •44. Степенной ряд, радиус сходимости.
- •45. Формула Коши-Адамара
- •46.Почленное дифференцирование и интегрирование степенных рядов.
- •47. Аналитические функции. Ряд Тейлора.
- •48. Ряды Тейлора основных элементарных функций.
- •49.Ряды Фурье по ортонормированной системе функций.
- •50. Интеграл Дирихле.
- •51. Сходимость рядов Фурье в точке(лемма 1)
- •52. Признак Дини и следствия из него
- •53. Суммирование рядов Фурье методом средних арифметических.
- •54. Теорема Фейера.
- •55. Теорема Вейерштрасса.
- •56. Неравенство Бесселя. Равенство Парсеваля.
- •57.Диф. Тригонометрических рядов Фурье.
- •58. Интегрирование рядов Фурье
- •59.Комплексная форма ряда Фурье.
1.Несобственные интегралы и их свойства.
Опр.:
Пусть ф-ция
![]() определена на промежутке
определена на промежутке![]() и интегрируема на любом отрезке
содержащемся в этом промежутке. Величина
и интегрируема на любом отрезке
содержащемся в этом промежутке. Величина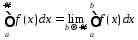 , если указанный предел существует,
называется несобственным интегралом
Римана от ф-ции
, если указанный предел существует,
называется несобственным интегралом
Римана от ф-ции![]() по промежутку
по промежутку![]() (НИ-1)
(НИ-1)
Опр.:
Пусть ф-ция
![]() определена на промежутке
определена на промежутке![]() и интегрируема на любом отрезке
и интегрируема на любом отрезке![]() .
Величина
.
Величина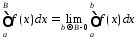 , если указанный предел существует,
называется несобственным интегралом
от ф-ции
, если указанный предел существует,
называется несобственным интегралом
от ф-ции![]() по промежутку
по промежутку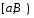 (НИ-2)
(НИ-2)
Теорема
1: Пусть
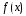 и
и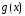 функции определенные на промежутке
функции определенные на промежутке![]() ,
интегрируемы на любом отрезке
,
интегрируемы на любом отрезке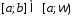 ,
и для них определены несобственные
интегралы
,
и для них определены несобственные
интегралы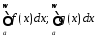 .
.
Тогда
1) Если
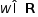 и
и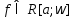 ,
то значения интеграла
,
то значения интеграла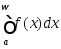 понимаемого как в несобственном, так и
в собственном смысле, совпадают.
понимаемого как в несобственном, так и
в собственном смысле, совпадают.
2)При
любых
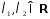 функция
функция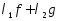 интегрируема в несобственном смысле
на
интегрируема в несобственном смысле
на![]() и справедливо равенство
и справедливо равенство
3)
Если
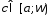 ,
то
,
то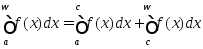
4)
Если
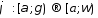 - гладкое, строго монотонное отображение,
причем
- гладкое, строго монотонное отображение,
причем
 и
и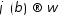 при
при ,
то несобств. интеграл от функции
,
то несобств. интеграл от функции существует и справедливо равенство
существует и справедливо равенство Док-во:
1)
Следует из непрер. Функции Ф(b)=
∫ab
f(x)dx
на отрезке [a;ω].
Док-во:
1)
Следует из непрер. Функции Ф(b)=
∫ab
f(x)dx
на отрезке [a;ω].
2) следует из того, что при b ϵ [a; w)
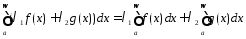
3) Следует из равенства
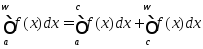
Справедливого при любых b,c ϵ [a; w).
4)
Следует
из формулы
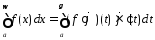
замены переменной в определенном интеграле.
Теорема 2. Если f,g €C1[a; w) и существует предел lim(f(x)•g(x))(x→w), то функции f•g' и f'•g одновременно интегрируемы или не интегрируемы в несобственном смысле на [a; w) и в случае интегрируемости справедливо равенство
 =
f (x)•g(x)|wa-
=
f (x)•g(x)|wa-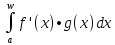 ,где
f(x) • g(x)|wa
= lim f (x)•g(x) - f(a)•g(a) (x→w).
,где
f(x) • g(x)|wa
= lim f (x)•g(x) - f(a)•g(a) (x→w).
2. Критерий Коши сходимости несобственных интегралов.
Сходимость несобственного интеграла равносильна существованию предела функции
 при
при
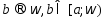
Теорема:
Если функция
![]() определена на промежутке
определена на промежутке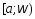 и интегрируема на любом отрезке
и интегрируема на любом отрезке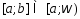 ,
то интеграл
,
то интеграл сходится тогда и только тогда, когда
для любого
сходится тогда и только тогда, когда
для любого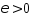 можно указать
можно указать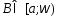 так, что при любых
так, что при любых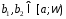 таких, что
таких, что ,
имеет место соотношение
,
имеет место соотношение
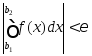
Доказательство:
Поскольку
 ,
то выписанное условие есть критерий
Коши существования предела функции
,
то выписанное условие есть критерий
Коши существования предела функции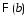 при
при
3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
Опр.:
Несобственный интеграл
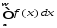 (1)
называется абсолютно сходящимся, если
сходится интеграл
(1)
называется абсолютно сходящимся, если
сходится интеграл![]() (2).
Функции, для которых интеграл
(2).
Функции, для которых интеграл![]() абсолютно сходится, называются абсолютно
интегрируемыми на промежутке с концами
абсолютно сходится, называются абсолютно
интегрируемыми на промежутке с концами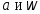
Теорема: Абсолютно сходящийся несобственный интеграл является сходящимся.
Доказательство.
Ввиду того, что задан несобственный
интеграл
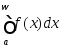 (1),
сужение функции
(1),
сужение функции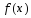 интегрируемо по Риману на любом отрезке
интегрируемо по Риману на любом отрезке .
Отсюда по св-ву модуля определенного
интеграла устанавливаем, что
.
Отсюда по св-ву модуля определенного
интеграла устанавливаем, что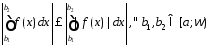 .
Несобственный интеграл
.
Несобственный интеграл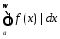 сходится. Тогда по критерию Коши
сходимости несобственного интеграла
сходится. Тогда по критерию Коши
сходимости несобственного интеграла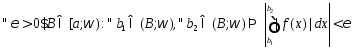
Из
приведенных выше соотношений по критерию
Коши следует, что несобственный интеграл
 сходится.
сходится.
Следствие 1: Если НИ (1) расходится, то расх и НИ (2).
Опр: Если НИ (1) сходится, а НИ (2) расх, то НИ (1) называется условно сходящимся.
Теорема
5. Если
функция f(x)
определена на [a;w),
интегрируема на каждом отрезке [a;b]
€[a;w)иf(x)>=0
на [a;w),
то несобственный интеграл (1) сходится
тогда и только тогда, когда функция
 ограничена[a;w).
ограничена[a;w).
Доказательство.
Действительно,
если f(x)>=
0на
[a;w),то
функция
 неубывающая
на[a;w)и
потому она имеет предел при b→w,b€[a;w)если
и только если она ограничена. □
неубывающая
на[a;w)и
потому она имеет предел при b→w,b€[a;w)если
и только если она ограничена. □
Теорема 6 (признак сравнения). Пусть функции f(x),g(x) определены на промежутке [a;w), неотрицательны и интегрируемы на любом отрезке [a;b] €[a;w). Если функция f(x) ограничена по сравнению с функцией g(x) при x→w, то:
а) из
сходимости интеграла
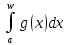 следует
сходимость интеграла
следует
сходимость интеграла ;
;
б) из
расходимости интеграла
 следует расходимость интеграла
следует расходимость интеграла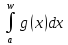 .
.
Док-во: То, что f(x)=O(g(x)) при x→w, означает наличие некоторого числа ῆ ϵ [a;w), при котором справедливо соотношение f(x)≤L g(x), A xϵ [ῆ; w), где L – нек. пол.пост.
Определенные
интегралы F(b)=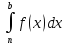 и
G(x)=
и
G(x)=
где bϵ[ῆ;w) на основании свойств интегрирования неравенств и линейности, а также оценки f(x)≤L g(x), A xϵ [ῆ; w) связаны соотношением f(b)≤L g(b), A bϵ [ῆ; w).
а)
Пусть интеграл
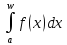 сходится.
А значит и сходится интеграл
сходится.
А значит и сходится интеграл
 .
Сужение функцииg(x)
на промежуток
.
Сужение функцииg(x)
на промежуток
[ῆ;
w)
знакоположительно на нем, и по теореме
5
функция G(b)
ограничена сверху на [ῆ; w).
Учитывая, что L
- вещ. полож. число, из неравенства f(b)≤L
g(b),
A
bϵ
[ῆ; w)
следует ограниченность на [ῆ; w)
знакоположительной функции F(b).
Следовательно (на осн.теоремы5)
несобственный интеграл
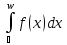 сходится. Поскольку
сходится. Поскольку
 =
=
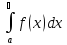 +
+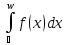 ,
,
а
интеграл
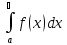 определенный, заключаем, что
определенный, заключаем, что сходится.
сходится.
б)
Пусть несобственный интеграл
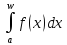 расходится.
Допустим противное, что интеграл
расходится.
Допустим противное, что интеграл
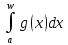 сходится.
Однако, если интеграл
сходится.
Однако, если интеграл сходится, то по доказанному выше
несобственный интеграл
сходится, то по доказанному выше
несобственный интеграл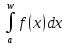 является
сходящимся. Получили противоречие.
является
сходящимся. Получили противоречие.
