
- •Вопросы к зачету для заочного отделения по курсу
- •II. Векторная алгебра.
- •III. Аналитическая геометрия.
- •IV. Математический анализ
- •I. Линейная алгебра Матрицы Прямоугольная таблица чисел
- •Пример. Даны матрицы а и в. ;. Найти произведение матриц ав.
- •Определители.
- •Методы решения систем линейных уравнений.
- •Обратная матрица.
- •Решение систем уравнений матричным методом.
- •Ранг матрицы.
- •Окаймляем его слева и снизу
- •Окаймляем d3 ( это только можно сделать двумя способами)
- •Прямоугольные системы уравнений.
- •Собственные векторы и собственные значения матрицы.
- •II. Векторная алгебра.
- •Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль, равный единице. Прямоугольные координаты
- •III. Аналитическая геометрия Аналитическая геометрия на плоскости
- •Если две прямые заданы уравнениями с угловым коэффициентом
- •Если уравнения прямых заданы в общем виде
- •Приведем уравнение прямой к нормальному виду. Нормирующий множитель
- •Аналитическая геометрия в пространстве
- •Уравнение плоскости в нормальном виде
- •Уравнение плоскости в отрезках на осях
- •Угол между двумя плоскостями
- •Острый угол между прямой иплоскостью
- •Кривые второго порядка.
- •Простейшее уравнение гиперболы
- •Асимптоты гиперболы - две прямые, определяемые уравнениями
- •Простейшее уравнение параболы
- •IV. Математический анализ Функция одной переменной
- •Предел функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •Непрерывность функции
- •Дифференциальное исчисление. Производная. Техника дифференцирования. Обозначение
- •Производная сложной функции
- •Параметрически заданные функции и их дифференцирование
- •Правило Лопиталя
- •Применение дифференциального исчисления к исследованию функций
- •Признаки возрастания и убывания функций
- •Максимум и минимум функции
- •Первое достаточное условие существования экстремума функции
- •Второе достаточное условие существования экстремума
- •Асимптоты.
- •Общее исследование функции
Производная сложной функции
Если
у = f(u) и u = u(x), то есть
![]() - сложная функция , причем функции у =
f(u) и u = u(x) дифференцируемые, то
- сложная функция , причем функции у =
f(u) и u = u(x) дифференцируемые, то![]() .
Аргумент u часто называют промежуточной
переменной. Это правило выполняется
для сложной функции, которая имеет
конечное число промежуточных аргументов.
Если, например, у = f(u) и u = u(v), v=v(x), то
.
Аргумент u часто называют промежуточной
переменной. Это правило выполняется
для сложной функции, которая имеет
конечное число промежуточных аргументов.
Если, например, у = f(u) и u = u(v), v=v(x), то![]() ,
если f(u) , u(v) и v(x) - дифференцируемые.
,
если f(u) , u(v) и v(x) - дифференцируемые.
Формулы дифференцирования основных функций
1.![]() 8.
8.![]()
2.![]() ,
,![]() 9.
9.![]() ,
,![]()
3.![]() 10.
10.![]()
4.![]() 11.
11.![]()
5.![]()
6.![]() 12.
12.![]()
7.![]() 13.
13.![]()
Примеры. Найти производные функций:
1. у = х4 – 2х3 + 3х + 1
Решение.
Используя правила и формулы
дифференцирования, получаем:
![]() (х4
– 2х3 + 3х + 1)' =
(х4
– 2х3 + 3х + 1)' =![]() =
=![]() .
.
2.
![]()
Решение.
Поскольку
![]() ,
то
,
то![]() =
=![]() .
.
3.
![]()
Решение.
Имеем произведение функций, поэтому
![]()
4.
![]()
Решение. Данная функций является сложной: у = f(u) , u = u(x), где u = х2 + 2х..
![]()
Дифференцирование неявно заданных функций
Равенство
![]() обозначает у как неявную и дифференцированную
функцию от х. Продифференцировав по х
обе части равенства, получим линейное,
относительно
обозначает у как неявную и дифференцированную
функцию от х. Продифференцировав по х
обе части равенства, получим линейное,
относительно![]() равенство, из которого получим значение
равенство, из которого получим значение![]() .
.
Пример.
Найти
![]() ,
если у > -5:
,
если у > -5:
![]() (1)
(1)
Решение.
Поскольку у функция от х, то у2 – сложная
функция и
![]() .
Продифференцируем обе части равенства
по х:
.
Продифференцируем обе части равенства
по х:
![]() (2)
(2)
Подставляя в равенство (1) х = 0, получим
![]()
откуда
![]()
Поскольку
у > -5, то
![]() .
Используя (2), имеем
.
Используя (2), имеем![]() .
.
Логарифмическое дифференцирование
Логарифмической производной функции у = f(x) называется производная от логарифма этой функции:
![]()
В
некоторых случаях предварительное
логарифмирование значительно упрощает
дифференцирование функции, а для функции
вида
![]() есть
единственно возможным способом
дифференцирования.
есть
единственно возможным способом
дифференцирования.
Примеры:
Найти
производную функции
![]() .
.
Решение: Логарифмируя обе части равенства получаем
![]() ,
откуда
,
откуда
![]() .
.
Поэтому,
![]()
![]() =
=![]()
![]() =
=![]()
Найти
производную показательно-степенной
функции
![]() .
.
Решение:
Имеем
![]()
![]()
![]()
![]() =
=
=
=![]()
Производные высших порядков.
Производную
![]() или
или![]() называют производной первого порядка
функции f(x). Производная
называют производной первого порядка
функции f(x). Производная![]() называется
производной второго порядка и обозначается
одним из символов:
называется
производной второго порядка и обозначается
одним из символов:![]() .
В общем виде производную n –го порядка
(или n-ой производной) называется
производная от производной порядка (n
– 1), то есть
.
В общем виде производную n –го порядка
(или n-ой производной) называется
производная от производной порядка (n
– 1), то есть![]() .
Обозначения, например:
.
Обозначения, например:![]() .
.
Пример. Найти производную n –го порядка функции у = cos x.
Решение. Последовательно дифференцируя, получим:
у
= cos x = сos(x+0![]() )
)
![]() x
= cos(x+1
x
= cos(x+1![]() )
)
![]() x
= cos(x+2
x
= cos(x+2![]() )
)
![]() x
= cos(x+3
x
= cos(x+3![]() )
)
……………………………….
![]() cos(x+n
cos(x+n![]() ),
n=
),
n=![]()
Параметрически заданные функции и их дифференцирование
Первую производную функции, заданной параметрически
![]()
находим
по формуле
![]() .
.
Вторую
производную удобно вычислять по формуле:
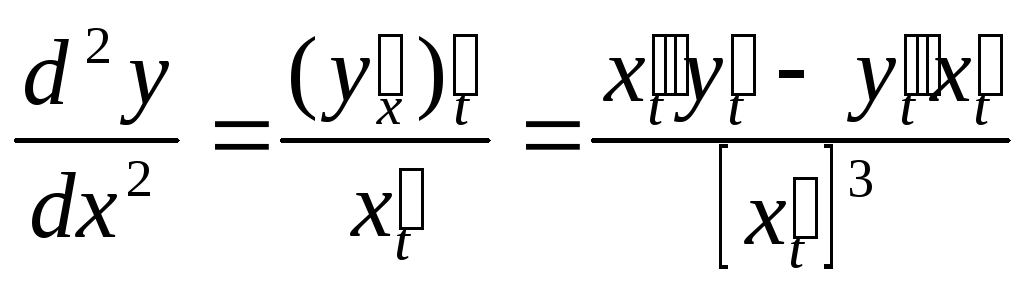 .
.
Пример.
Найти производную второго порядка
функции
![]()
Решение.
Согласно формуле:![]()
Далее,
![]() .
.
Правило Лопиталя
Правило Лопиталя дает возможность раскрыть некоторые виды неопределенности, используя производную. Оно основывается на данной ниже теореме.
Теорема.
Пусть функции
![]() и
и![]() определенные
и дифференцируемые в окружности точки
определенные
и дифференцируемые в окружности точки![]() ,
за исключением, возможно, самой точки
а, и пусть
,
за исключением, возможно, самой точки
а, и пусть![]() в
этой окружности. Если функции
в
этой окружности. Если функции![]() и
и![]() являются
одновременно бесконечно малыми или
бесконечно большими при
являются
одновременно бесконечно малыми или
бесконечно большими при![]() и
к тому же существует отношение производных
и
к тому же существует отношение производных![]() ,
то существует также предел
,
то существует также предел![]() ,
причем эти пределы равны между собой:
,
причем эти пределы равны между собой:![]() =
=![]() .
.
Теорема
справедлива и в том случае, когда
![]() .
Если производные
.
Если производные![]() и
и![]() ,
n > 2, удовлетворяют тем же самым условиям,
что и функции
,
n > 2, удовлетворяют тем же самым условиям,
что и функции![]() и
и![]() ,
то
,
то![]() =
=![]() .
.
Теорема
дает возможность раскрыть неопределенность
типа
![]() ,
которые будем называть основными. Чтобы
раскрыть неопределенности типа 0,
,
которые будем называть основными. Чтобы
раскрыть неопределенности типа 0,![]() необходимо вначале привести их к основным
и применить правило Лопиталя.
необходимо вначале привести их к основным
и применить правило Лопиталя.
Пример.
1.
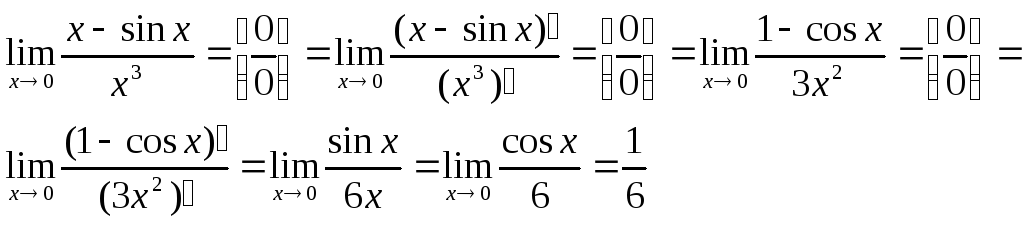
2.
 =
=![]()
3.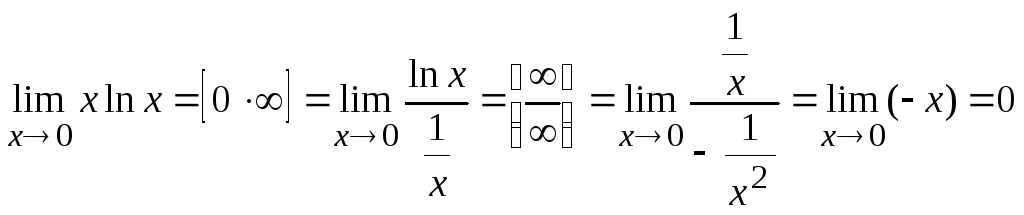
4.
![]()
5.
![]()

Откуда,
![]() .
.
6.
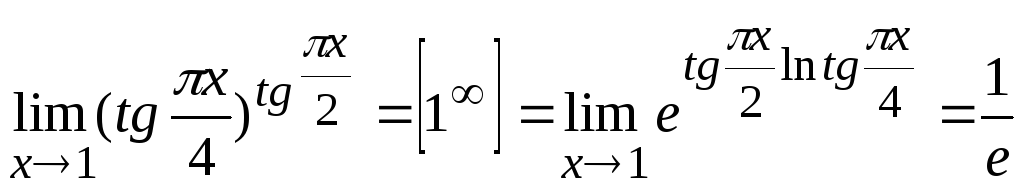 ,
действительно,
,
действительно,
![]()
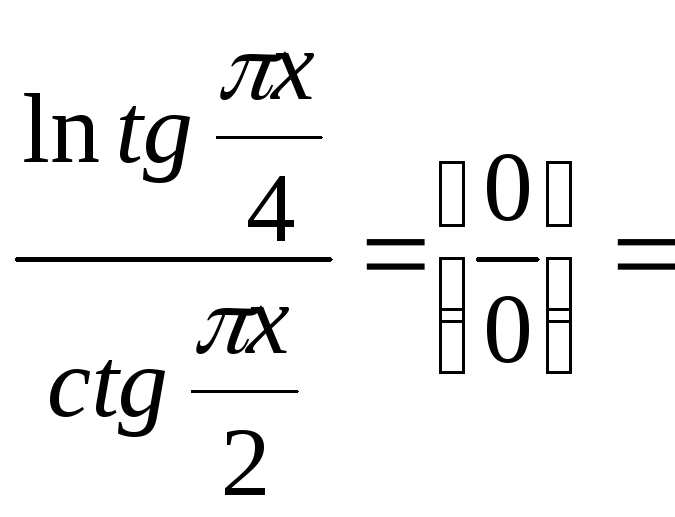
![]()
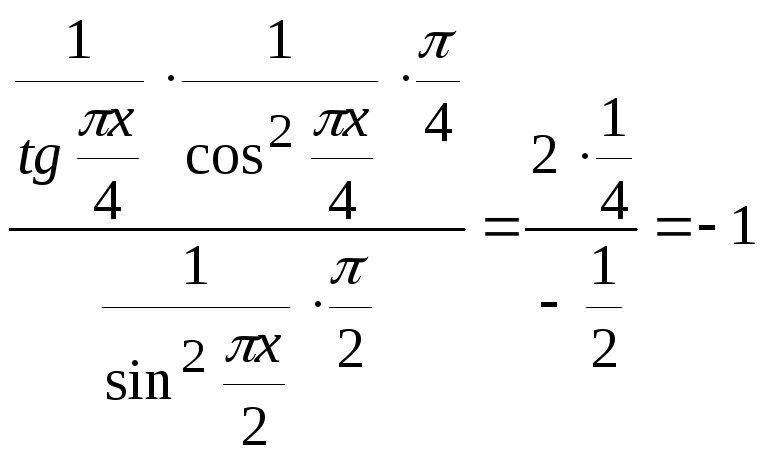 .
.
Напомним,
что во многих случаях пользуемся
равенством
![]() .
.
